A student connects four cells, each of emf 1.5 V and internal resistance 0.25Ω in series but one cell has its terminals reversed. This battery sends current in a 2Ω resistor . What will be the current ?
2A
4A
1A
3A
The correct Answer is:C
To solve the problem, we need to find the current flowing through a circuit consisting of four cells connected in series, with one cell having its terminals reversed. Here’s a step-by-step solution:
Step 1: Determine the total EMF of the battery
Each cell has an EMF of 1.5 V. Since there are four cells, the total EMF would normally be:
Total EMF=1.5V+1.5V+1.5V+1.5V=6V
However, since one cell is reversed, we subtract the EMF of that cell:
Net EMF=6V−1.5V=4.5V
Step 2: Calculate the total internal resistance
Each cell has an internal resistance of 0.25Ω. Since all four cells are in series, their internal resistances add up:
Total Internal Resistance=0.25Ω+0.25Ω+0.25Ω+0.25Ω=1Ω
Step 3: Add the external resistance
The external resistor is given as 2Ω. Therefore, the total resistance in the circuit is:
Total Resistance=Total Internal Resistance+External Resistance=1Ω+2Ω=3Ω
Step 4: Calculate the current using Ohm's Law
Using Ohm's Law, the current I can be calculated as:
I=Net EMFTotal Resistance=4.5V3Ω=1.5A
Final Answer
The current flowing through the circuit is 1.5A.
---
Each cell has an EMF of 1.5 V. Since there are four cells, the total EMF would normally be:
Each cell has an internal resistance of 0.25Ω. Since all four cells are in series, their internal resistances add up:
The external resistor is given as 2Ω. Therefore, the total resistance in the circuit is:
Using Ohm's Law, the current I can be calculated as:
The current flowing through the circuit is 1.5A.
Similar Questions
Three identical cells, each of emf 2 V and internal resistance 0.2Ω are connected in series to an external resistor of 7.4Ω. Calculate the current in the circuit.
View SolutionHow you would arrange 24 cells, each of emf 1.5V and internal resistance 0.5Ω, to deliver maximum current to a resistor of 4Ω? What is the maximum current?
View Solution
Knowledge Check
A battery of 24 cells each of emf 1.5 V and internal resistnace 2Ω is to be connected in order to send the maximum current through a 12Ω resistor. The correct arrangement of cells will be
A2 rows of 12 cells connected in parallelB3rows of 8 cells connected in parallelC4 rows of 6 cells connected in parallelDAll of theseA person connects four 14Ω cells in series but one cell has its terminal reversed. The external resistance is 1Ω. If each cell has an emf of 1.5V, the currenet folowing is
A43AB34AC1.5ADzeron identical cells, each of emf e volt and internal resistance rΩ are connected in a row m. Such rows are connected in parallel. This battery sends current through an external resistance R. The current will be maximum if
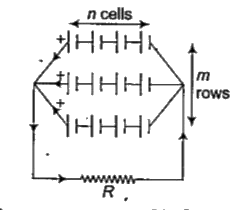 Anr=mRBnR=mrCnm=rRDnmR=r
Anr=mRBnR=mrCnm=rRDnmR=r
Thirty six cells each of emf 1.5 V and internal resistance 0.5Ω are used to send current through an external resistor of resistance 2Ω. What is the best mode of grouping them and the current through the external resistor
View Solution(a) Six lead-acid type of secondary cells, each of emf 2.0 V and internal resistance 0.015Ω are joined in series to provide a supply to a resistance of 8.5Ω. What are the currents drawn from the supply, and its terminal voltage?
(b) A secondary cell after long use has an emf 1.9 V and a large internal resistance of 380Ω. What maximum current can be drawn from the cell? Could the cell drive the starting motor of a car?
View SolutionArrange 32 identical cells of emf 2 V each with internal resistance 0.5Ω such current passing through an external resistance of 1Ω is maximum.
what will be the value of current ?
View SolutionA student is asked to connected four cells of emf of 1 V and internal resistance 0.5 ohm in series with an external resistance of 1 ohm. But one cells is wrongly connected by him with its terminal reversed, the current in the ciruit is
View Solution4 cells each of emf 2 V and internal resistance of 1Ω are connected in parallel to a load resistor of 2Ω. Then the current through the load resistor is
View Solution