4 cells each of emf 2 V and internal resistance of 1Ω are connected in parallel to a load resistor of 2Ω. Then the current through the load resistor is
2A
1.5A
1A
0.888A
The correct Answer is:D
To find the current through the load resistor when 4 cells (each with an EMF of 2 V and internal resistance of 1 Ω) are connected in parallel to a load resistor of 2 Ω, we can follow these steps:
Step 1: Calculate the total EMF and internal resistance of the cells in parallel
When cells are connected in parallel, the EMF remains the same as that of a single cell, while the total internal resistance (R_internal) can be calculated using the formula for resistors in parallel:
1Rtotal=1R1+1R2+1R3+1R4
For our case, since all internal resistances are equal (1 Ω):
1Rtotal=11+11+11+11=4
Thus,
Rtotal=14Ω=0.25Ω
Step 2: Determine the equivalent circuit
Now we have:
- EMF (E) = 2 V
- Total internal resistance (R_internal) = 0.25 Ω
- Load resistance (R_load) = 2 Ω
Step 3: Calculate the total resistance in the circuit
The total resistance (R_total) in the circuit is the sum of the internal resistance of the cells and the load resistance:
Rtotal=Rinternal+Rload=0.25Ω+2Ω=2.25Ω
Step 4: Calculate the total current in the circuit using Ohm's Law
Using Ohm's Law, the total current (I_total) flowing from the cells can be calculated as:
Itotal=ERtotal=2V2.25Ω=89A≈0.89A
Step 5: Calculate the current through the load resistor
Since the load resistor is in parallel with the internal resistances of the cells, the voltage across the load resistor is the same as the voltage across the internal resistances. The current through the load resistor (I_load) can be calculated using Ohm's Law:
Iload=VloadRload=E−Itotal⋅RinternalRload
First, we need to find the voltage across the load resistor:
Vload=E−Itotal⋅Rinternal=2V−(89A⋅0.25Ω)=2V−29V=169V
Now, substituting back to find the current through the load resistor:
Iload=VloadRload=169V2Ω=1618A=89A≈0.89A
Final Answer
The current through the load resistor is approximately 0.88A.
---
- EMF (E) = 2 V
- Total internal resistance (R_internal) = 0.25 Ω
- Load resistance (R_load) = 2 Ω
Topper's Solved these Questions
- CURRENT ELECTRICITY BOOK - MTG GUIDECHAPTER - CURRENT ELECTRICITY EXERCISE - CHECK YOUR NEET VITALS
16 Videos
- CURRENT ELECTRICITY BOOK - MTG GUIDECHAPTER - CURRENT ELECTRICITY EXERCISE - MCQs AIPMT / NEET
32 Videos
- CURRENT ELECTRICITY BOOK - MTG GUIDECHAPTER - CURRENT ELECTRICITY EXERCISE - MCQs AIPMT / NEET
32 Videos
- ATOMS AND NUCLEIBOOK - MTG GUIDECHAPTER - ATOMS AND NUCLEIEXERCISE - AIPMT/NEET(MCQs)
40 Videos
- DUAL NATURE OF MATTER AND RADIATION BOOK - MTG GUIDECHAPTER - DUAL NATURE OF MATTER AND RADIATION EXERCISE - AIPMT/ NEET MCQs
30 Videos
Similar Questions
Three identical cells, each of emf 2 V and internal resistance 0.2Ω are connected in series to an external resistor of 7.4Ω. Calculate the current in the circuit.
View SolutionThree identical, each of emf 2 V and internal resistance 0.2Ω are connected in series to an external resistor of 7.4Ω. Calculate the current in the circuit.
View Solution
Knowledge Check
Two cells of emf 1.25V,0.75V and each of internal resistance 1Ω are connected in parallel. The effective emf will be
A1 VB1.25 VC2 VD0.5 VA battery of 24 cells each of emf 1.5 V and internal resistnace 2Ω is to be connected in order to send the maximum current through a 12Ω resistor. The correct arrangement of cells will be
A2 rows of 12 cells connected in parallelB3rows of 8 cells connected in parallelC4 rows of 6 cells connected in parallelDAll of theseA 5V battery with internal resistance 2Ω and a 2V battery with internal resistance1Ω are connected to a 10Ω resistor as shown in the figure.

The current in the 10Ω resistor isA0.27AP2→P1B0.03AP1→P2C0.03AP2→P1D0.27AP1→P2
A battery of emf 6V internal resistance 5Ω is joined in parallel with another cell of emf of 10V and internal resistance 1Ω and the combination is used to send current through a resistor of 12Ω. Calculate the current through each battery.
View SolutionA dry cell of emf 1.6V and internal resistance of 0.10Ω is connected to a resistor of resistance Rω. If the current drawn the cell is 2A, then (i) What is the voltage drop across R ? (ii) What is the rate of energy dissipation in the resistor ?
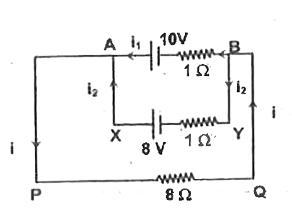
View SolutionTwo cells having emf's of 10 V and 8 V, and internal resistance of 1Ω(each) are connected as shown with an external resistance of 8Ω Find the current flowing through the circuit.
View SolutionA cell of emf 2V and internal resistance 4Ω is connected across a parallel combination of two resistors of resistance 10Ω and 20Ω. Find the current through each resistor using Kirchhoff's laws.
View SolutionA battery of e.m.f 10V and internal resistance 3Omega is connected to a resistor.If the current in the circuit is 0.5A,then the resistance of the resistor is
View Solution

