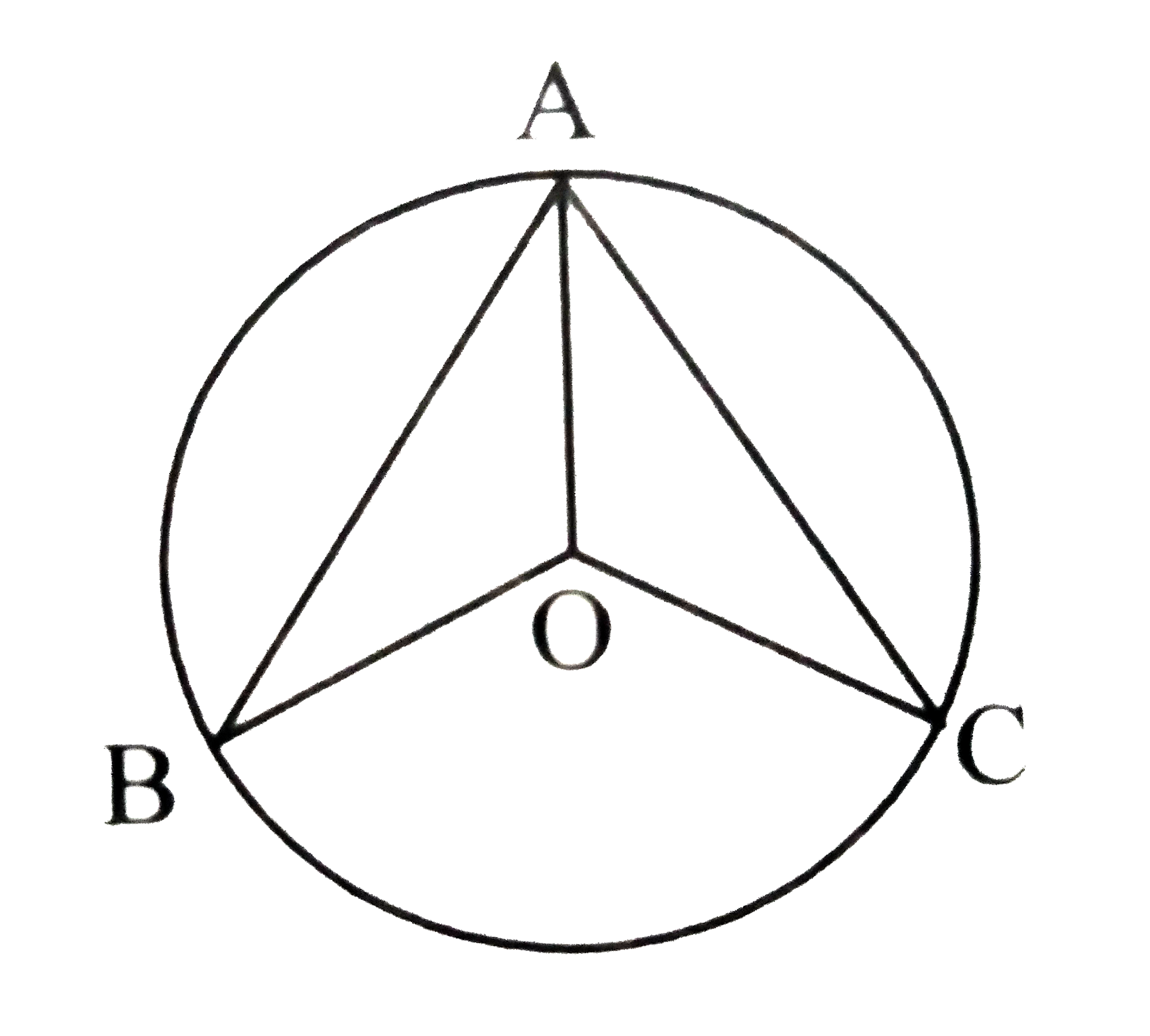
If A, B, C are three points on a circle with centre 'O' such that ∠AOB=90∘ and ∠BOC=120∘, then ∠ABC=
60∘
75∘
90∘
135∘
The correct Answer is:B
To find the angle ∠ABC given the angles ∠AOB=90∘ and ∠BOC=120∘, we can follow these steps:
Step 1: Understand the relationship between angles at the center and angles at the circumference
In a circle, the angle subtended at the center by an arc is twice the angle subtended at any point on the circumference by the same arc. This means if we have ∠AOC at the center, then ∠ABC at the circumference is given by the formula:
∠ABC=12∠AOC
Step 2: Calculate ∠AOC
We know that the sum of angles around point O is 360∘. Therefore, we can find ∠AOC using the following equation:
∠AOB+∠BOC+∠AOC=360∘
Substituting the known values:
90∘+120∘+∠AOC=360∘
This simplifies to:
210∘+∠AOC=360∘
Now, isolate ∠AOC:
∠AOC=360∘−210∘=150∘
Step 3: Find ∠ABC
Now that we have ∠AOC=150∘, we can find ∠ABC:
∠ABC=12∠AOC=12×150∘=75∘
Conclusion
Thus, the value of ∠ABC is 75∘.
In a circle, the angle subtended at the center by an arc is twice the angle subtended at any point on the circumference by the same arc. This means if we have ∠AOC at the center, then ∠ABC at the circumference is given by the formula:
∠ABC=12∠AOC
We know that the sum of angles around point O is 360∘. Therefore, we can find ∠AOC using the following equation:
∠AOB+∠BOC+∠AOC=360∘
Substituting the known values:
90∘+120∘+∠AOC=360∘
This simplifies to:
210∘+∠AOC=360∘
Now, isolate ∠AOC:
∠AOC=360∘−210∘=150∘
Now that we have ∠AOC=150∘, we can find ∠ABC:
∠ABC=12∠AOC=12×150∘=75∘
Thus, the value of ∠ABC is 75∘.
Similar Questions
Knowledge Check
Assertion (A) : PA and PB are triangles to a circle with centre O such that ∠AOB=110∘, then ∠APB=90∘
Reason (R ) : The length of two tangents drawn from an external point are equal .ABoth A and R are true and R is the correct explanation for A.BBoth A and R are true and R is not correct explanation for A.CA is true but R is false.DA is false but R is true.In figure, if ∠AOB=90∘and∠ABC=30∘, then∠CAO is equal to
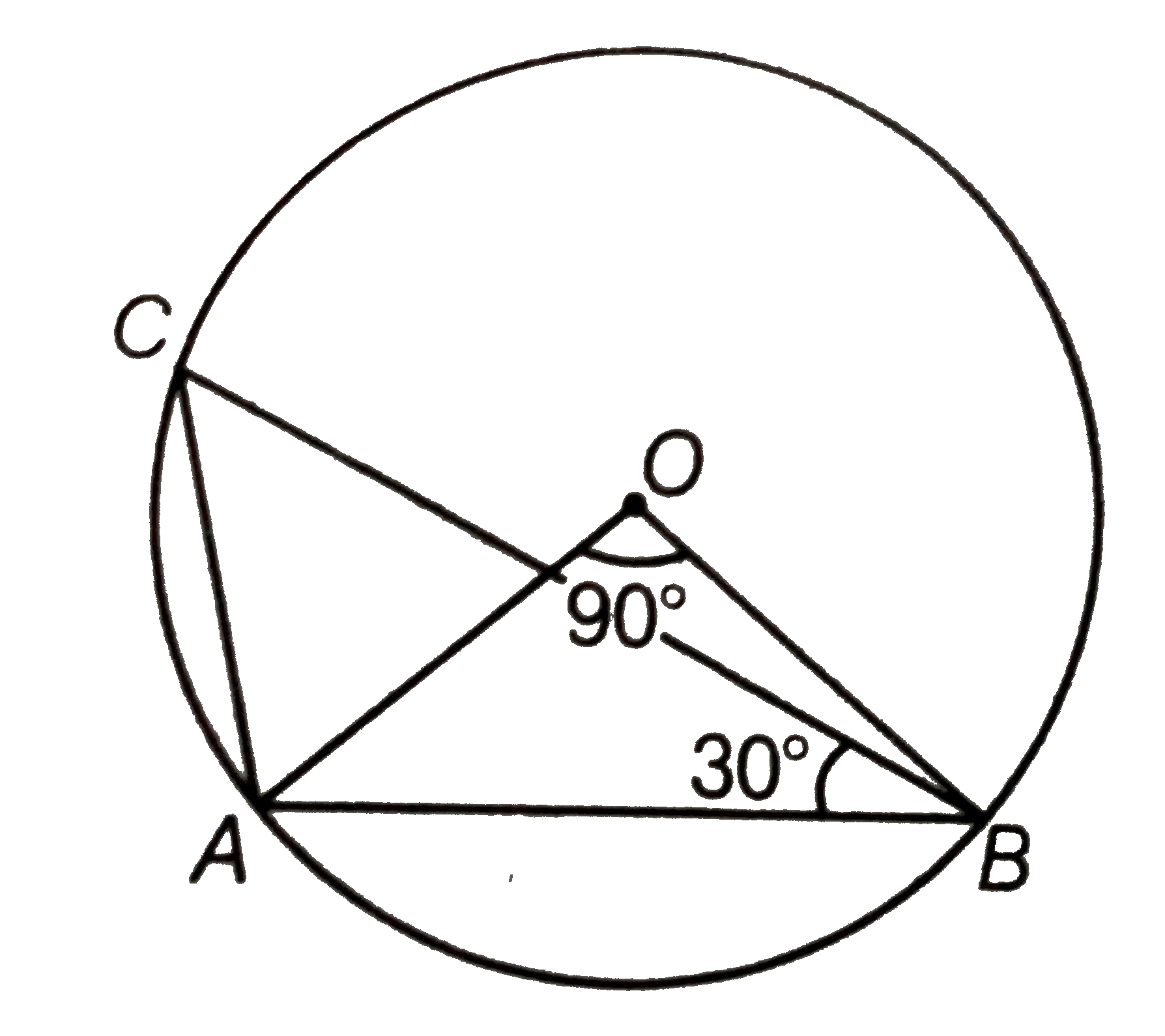 A30∘B45∘C90∘D60∘
A30∘B45∘C90∘D60∘O is the centre of a circle ∠AOB=90∘and∠BOC=120∘.∠ABC is equal to
 A150∘B210∘C75∘D105∘
A150∘B210∘C75∘D105∘
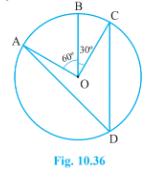
In Fig. 10.36, A,B and C are three points on a circle with centre O such that ∠BOC= 30o and ∠AOB= 60o. If D is a point on the circle other than the arc ABC, find ∠ADC.
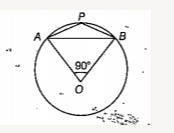
View SolutionIn the given figure, O is the centre of the circle∠AOB=90∘ Find m∠APB
View SolutionCE and DE are equal chords of a cricule with centre O. if ∠AOB=90∘find ar(△CED)ar(△AOB)
View SolutionO is the centre of a circle. AC and BD are two chords of the circle intersecting each other at P, If ∠AOB=15∘and∠APB=30∘, then ∠COD is equal to
View SolutionIf PQ and PR be the two tangents to a circle with centre O such that ∠QPR=120∘ then ∠POQ is
View Solution