ΔABCandΔDBC are equal in area and the points A and D lie on the same side of BC . Then
AD is perpendicular to AB
AD is parpendicular to DC
AD is parallel to BC
AD is parallel to the line passing through the point of intersection of AC and BD
The correct Answer is:C
To solve the problem, we will analyze the given information about triangles ABC and DBC, which are equal in area and have points A and D on the same side of line BC.
1. Understand the Given Information:
We have two triangles, ΔABC and ΔDBC, which are equal in area. Points A and D are located on the same side of line BC.
2. Draw the Triangles:
Start by sketching triangle ABC with vertices A, B, and C. Then, sketch triangle DBC with vertices D, B, and C. Note that BC is the common base for both triangles.
3. Identify the Base and Heights:
In both triangles, the base BC is the same. Let the height from point A to line BC be H1, and the height from point D to line BC be H2.
4. Write the Area Formulas:
The area of triangle ABC can be expressed as:
AreaABC=12×BC×H1
The area of triangle DBC can be expressed as:
AreaDBC=12×BC×H2
5. Set the Areas Equal:
Since the areas of the two triangles are equal, we can set the area formulas equal to each other:
12×BC×H1=12×BC×H2
6. Simplify the Equation:
We can cancel out 12 and BC (assuming BC≠0) from both sides:
H1=H2
7. Interpret the Result:
The equality H1=H2 means that the perpendicular distances from points A and D to line BC are equal. This indicates that both points A and D are at the same distance from line BC.
8. Conclude About the Lines:
Since A and D are at the same distance from line BC and lie on the same side of it, the line segment AD must be parallel to line BC.
Thus, we conclude that line AD is parallel to line BC.
Final Answer:
The correct conclusion is that line AD is parallel to line BC.
We have two triangles, ΔABC and ΔDBC, which are equal in area. Points A and D are located on the same side of line BC.
Start by sketching triangle ABC with vertices A, B, and C. Then, sketch triangle DBC with vertices D, B, and C. Note that BC is the common base for both triangles.
In both triangles, the base BC is the same. Let the height from point A to line BC be H1, and the height from point D to line BC be H2.
The area of triangle ABC can be expressed as:
AreaABC=12×BC×H1
The area of triangle DBC can be expressed as:
AreaDBC=12×BC×H2
Since the areas of the two triangles are equal, we can set the area formulas equal to each other:
12×BC×H1=12×BC×H2
We can cancel out 12 and BC (assuming BC≠0) from both sides:
H1=H2
The equality H1=H2 means that the perpendicular distances from points A and D to line BC are equal. This indicates that both points A and D are at the same distance from line BC.
Since A and D are at the same distance from line BC and lie on the same side of it, the line segment AD must be parallel to line BC.
The correct conclusion is that line AD is parallel to line BC.
Similar Questions
ΔABCandΔDBC are on same base BC and their vertices A and D are on opposite sides of BC. It is given that:
area of ΔABC= area of ΔDBC
Prove that BC bisects the line segment AD.
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E show that
View Solution
Knowledge Check
ΔABC is an equilateral triangle and D and E are midpoints of AB and BC respectively. Then the area of ΔABC : the area of the trapezium ADEC is
A5:3B4:1C8:5D4:3Two right triangles ABC and DBC are drawn on the same hypotenues BC on the same side of BC. If AC and DB intersects at P, then :
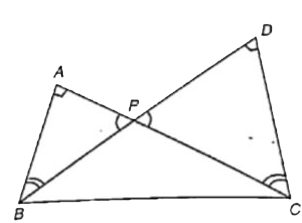 AAPPC=BPDPBAP×DP=PC×BPCAP×PC=BP×DPDAP×BP=PC×PD
AAPPC=BPDPBAP×DP=PC×BPCAP×PC=BP×DPDAP×BP=PC×PD
ABC and DBC are both isosceles triangles on a common base BC such that A and D lie on the same side of BC. Are triangles ADB and ADC congruent? Which condition do you use? If ∠BAC=400 and ∠BDC =1000; then find ∠ADB
View SolutionABC and DBC are two triangle on the same base BC such that A and D lie on the opposite sides of BC,AB=AC and DB =DC ,Show that AD is the perpedicular bisector of BC.
View SolutionIn parallelogram ABCD, P is a point on side AB and Q is a point on side BC, prove that
(i) ΔCPDandΔAQD are equal in area.
(ii) area (ΔAQD)= area of ΔAPD+ area of ΔCPB
View SolutionTwo triangles ABC and DBC are on the same base BC and on the same side of BC in which ∠A=∠D=90∘. If CAandBD meet each other at E, show that AE.EC=BE.ED.
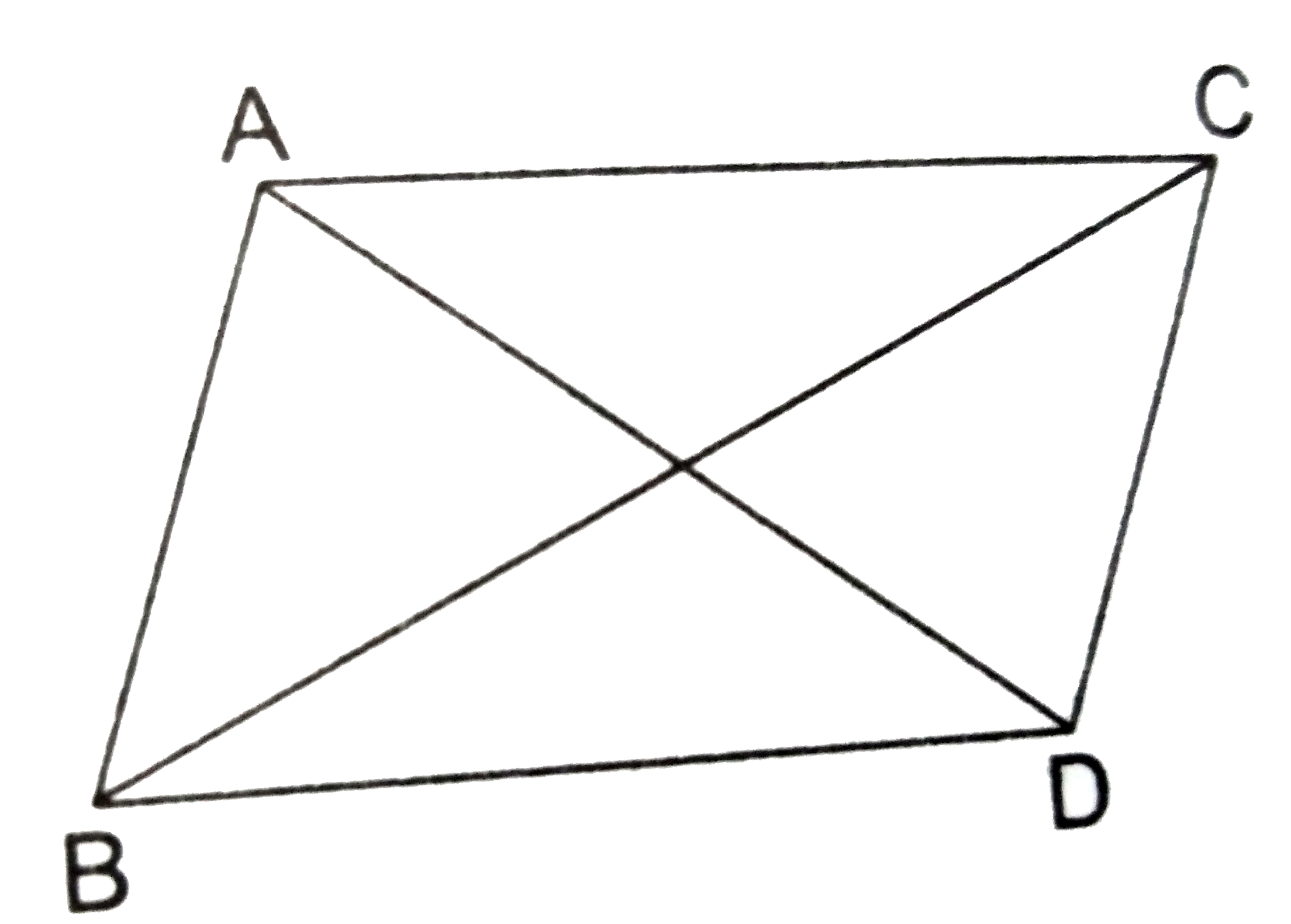
View SolutionIn the adjoining figure, △ABCand△DBC are on the same base BC with A and D on opposite sides of BC such that ar(△ABC)=ar(△DBC). Show that BC bisect AD.
View SolutionAn equilateral triangle ABC and a scalene triangle DBC are inscribed in a circle on same side of the arc. What is ∠BDC equal to?
View Solution
