Two triangles ABC and DBC are on the same base BC and on the same side of BC in which ∠A=∠D=90∘. If CAandBD meet each other at E, show that AE.EC=BE.ED.
Step by step video & image solution for Two triangles ABC and DBC are on the same base BC and on the same side of BC in which angle A= angle D=90^@. If CA and BD meet each other at E, show that AE. EC= BE. ED. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER-5 [UNSOLVED]EXERCISE - SECTION-D8videos
MODEL QUESTION PAPER-5 [UNSOLVED]
- BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER-5 [UNSOLVED]EXERCISE - SECTION-B7videos
MODEL QUESTION PAPER-5 [UNSOLVED]
- BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER-10 [UNSOLVED]EXERCISE - SECTION-D8videos
MODEL QUESTION PAPER-10 [UNSOLVED]
- BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER-6EXERCISE - SECTION-D7videos
MODEL QUESTION PAPER-6
Similar Questions
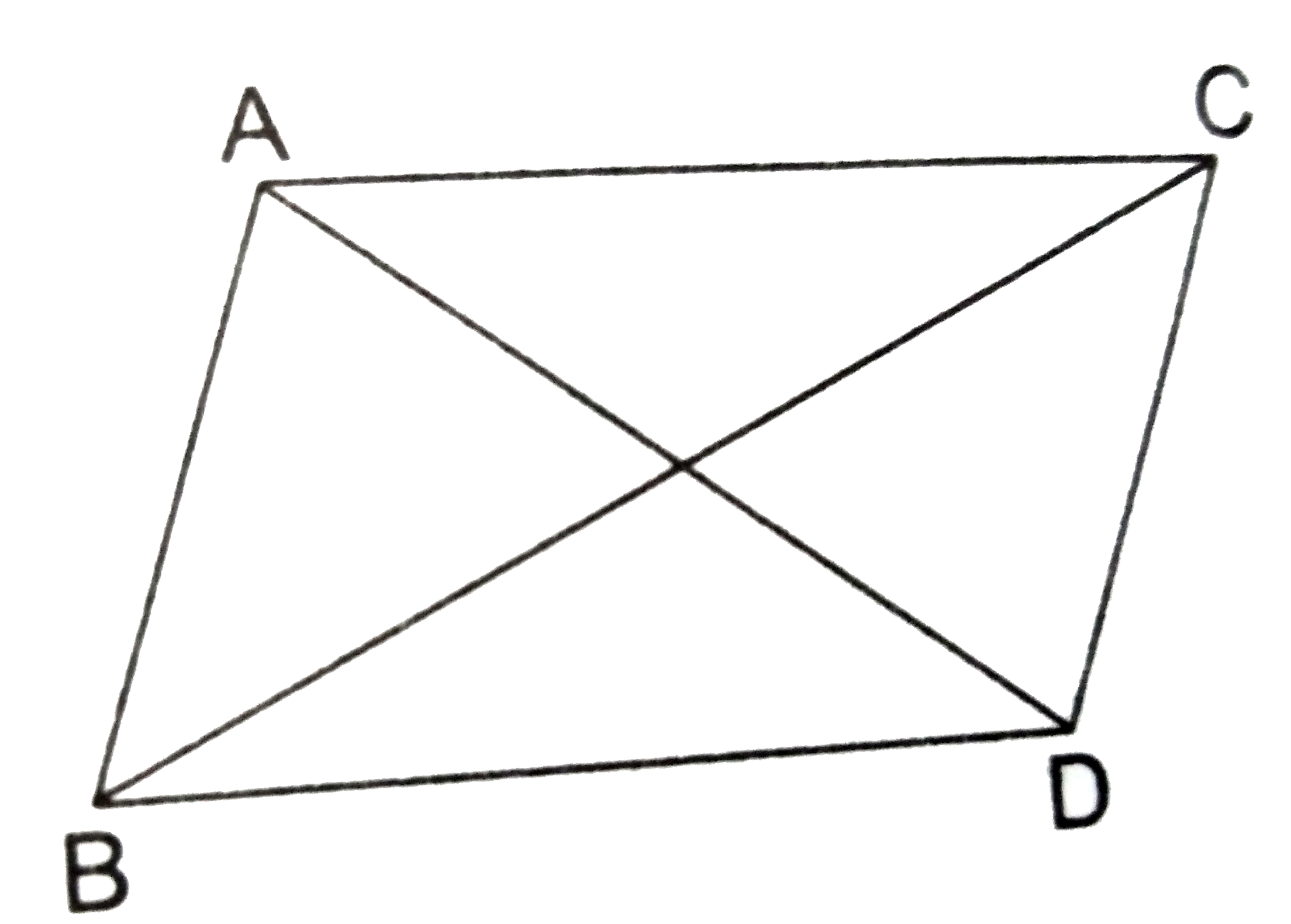
Two triangles BACandBDC , right angled at AandD respectively, are drawn on the same base BC and on the same side of BC . If AC and DB intersect at P, prove that AP⋅PC=DP⋅PB.
View SolutionIn the adjoining figure, △ABCand△DBC are on the same base BC with A and D on opposite sides of BC such that ar(△ABC)=ar(△DBC). Show that BC bisect AD.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two right triangles ABC and DBC are drawn on the same hypotenues BC on the same side of BC. If AC and DB intersects at P, then :
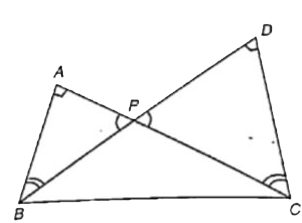 AAPPC=BPDPBAP×DP=PC×BPCAP×PC=BP×DPDAP×BP=PC×PD
AAPPC=BPDPBAP×DP=PC×BPCAP×PC=BP×DPDAP×BP=PC×PD
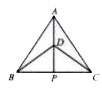
ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E show that
View SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E, show that
(i) ΔABD≅ΔACD
(ii) ΔABE≅ΔACE
(iii) AE bisects ∠A as well as ∠D
(iv) AE is the perpendicualr bisector of BC.
 View Solution
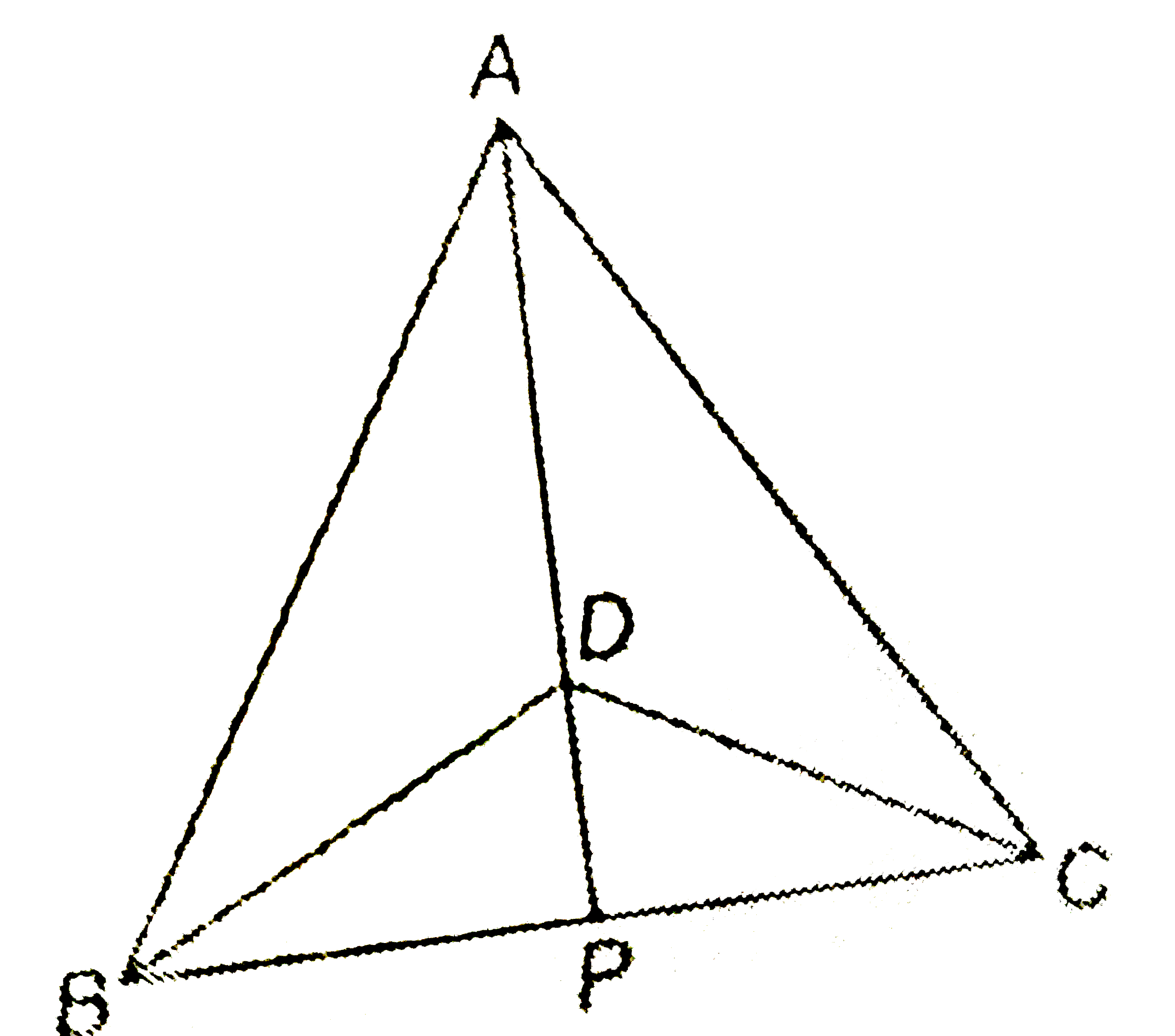
View SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that
AP bisects ∠A as well as ∠D.View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that :
(i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
 View Solution
View SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that

ΔABD≅ΔACDView SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that
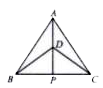
ΔABP≅ΔACPView Solution△ ABC and △ DBC are isosceles triangles on the same base BC. Prove that line AD bisects BC at right angles
View Solution
