ΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E, show that
(i) ΔABD≅ΔACD
(ii) ΔABE≅ΔACE
(iii) AE bisects ∠A as well as ∠D
(iv) AE is the perpendicualr bisector of BC.

(i) ΔABD≅ΔACDasAB=AC,BD=CD,AD=AD.
∴ ∠BAD∠CAD⇒∠BAE=∠CAE.
(ii) ΔABE≅ΔACEasAB=AC,AE=AE,∠BAE=∠CAE.
Similarly, ΔBDE≅ΔCDE.
(iii) ΔABE≅ΔACE⇒∠BAE=∠CAEand∠BDE=∠CDE.
(iv) BE=CEand∠AEB=90∘as∠AEB+∠AEC=180∘.
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Exercise 9B
Explore 16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Multiple Choice Questions (Mcq)
Explore 20 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Multiple Choice Questions (Mcq)
Explore 20 Videos
- CIRCLES Book:RS AGGARWALChapter:CIRCLES Exercise:MULTIPLE CHOICE QUESTION(MCQ)
Explore 37 Videos
- COORDINATE GEOMETRYBook:RS AGGARWALChapter:COORDINATE GEOMETRYExercise:Multiple Choice Questions (Mcq)
Explore 22 Videos
Similar Questions
ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E show that
View SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that

ΔABD≅ΔACD
View SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that
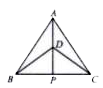
ΔABP≅ΔACP
View SolutionΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that :
(i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
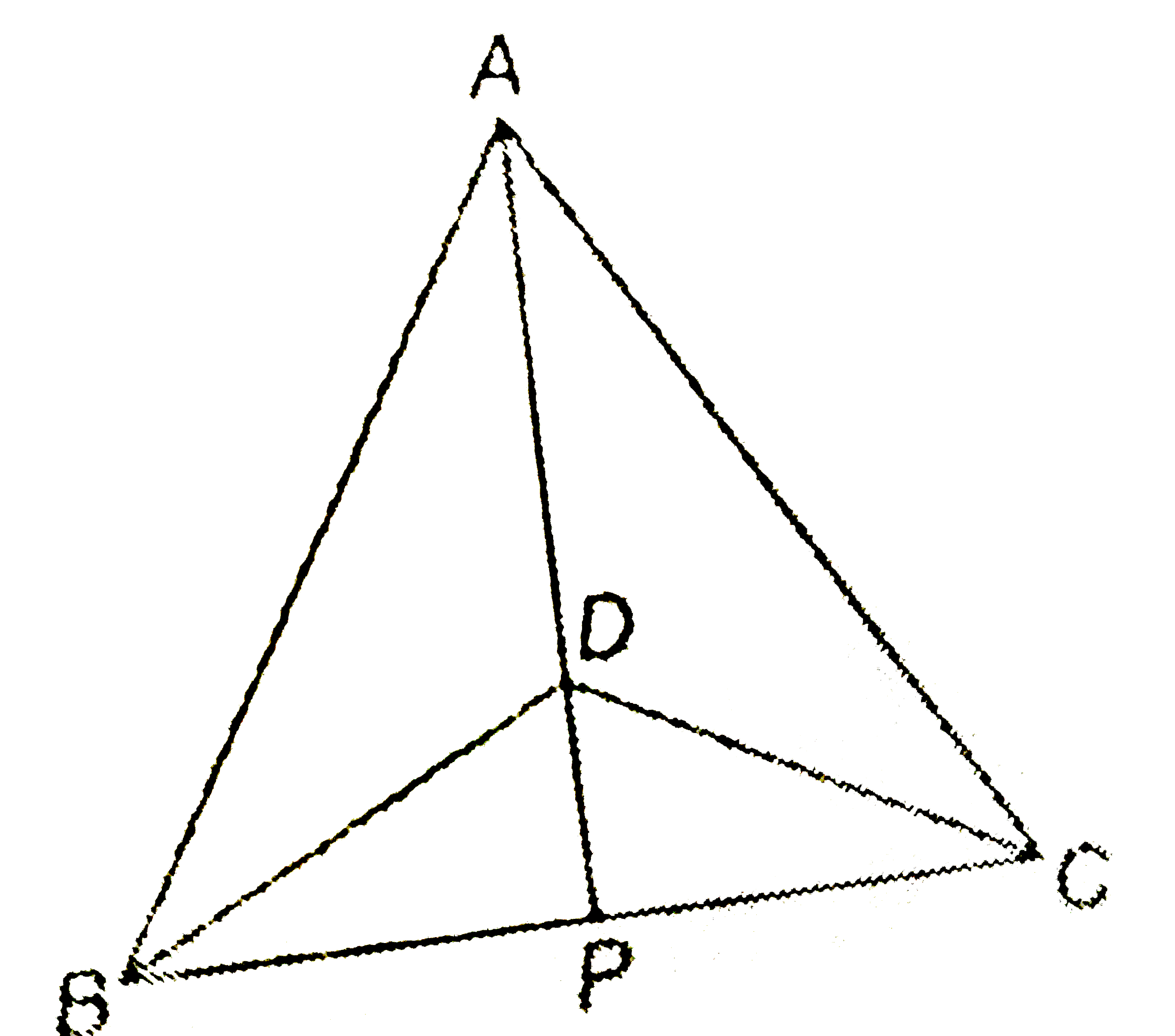
View SolutionΔABCand ΔDBCare two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC

View SolutionΔABCandΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that
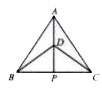
AP bisects ∠A as well as ∠D.
View Solution△ABC and △DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that (i) △ABD≅△ACD (ii) △ABP≅△ACP (iii) AP bisects ∠A as well as △D. (iv) AP is the perpendicular bisector of BC.
View SolutionABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that∠ABD =∠ACD

View SolutionIn the same figure, ΔABCandΔDBC are on the same base BC . If AD is intersects BC at O, prove that
ar(ΔABC)ar(ΔDBC)=AODO
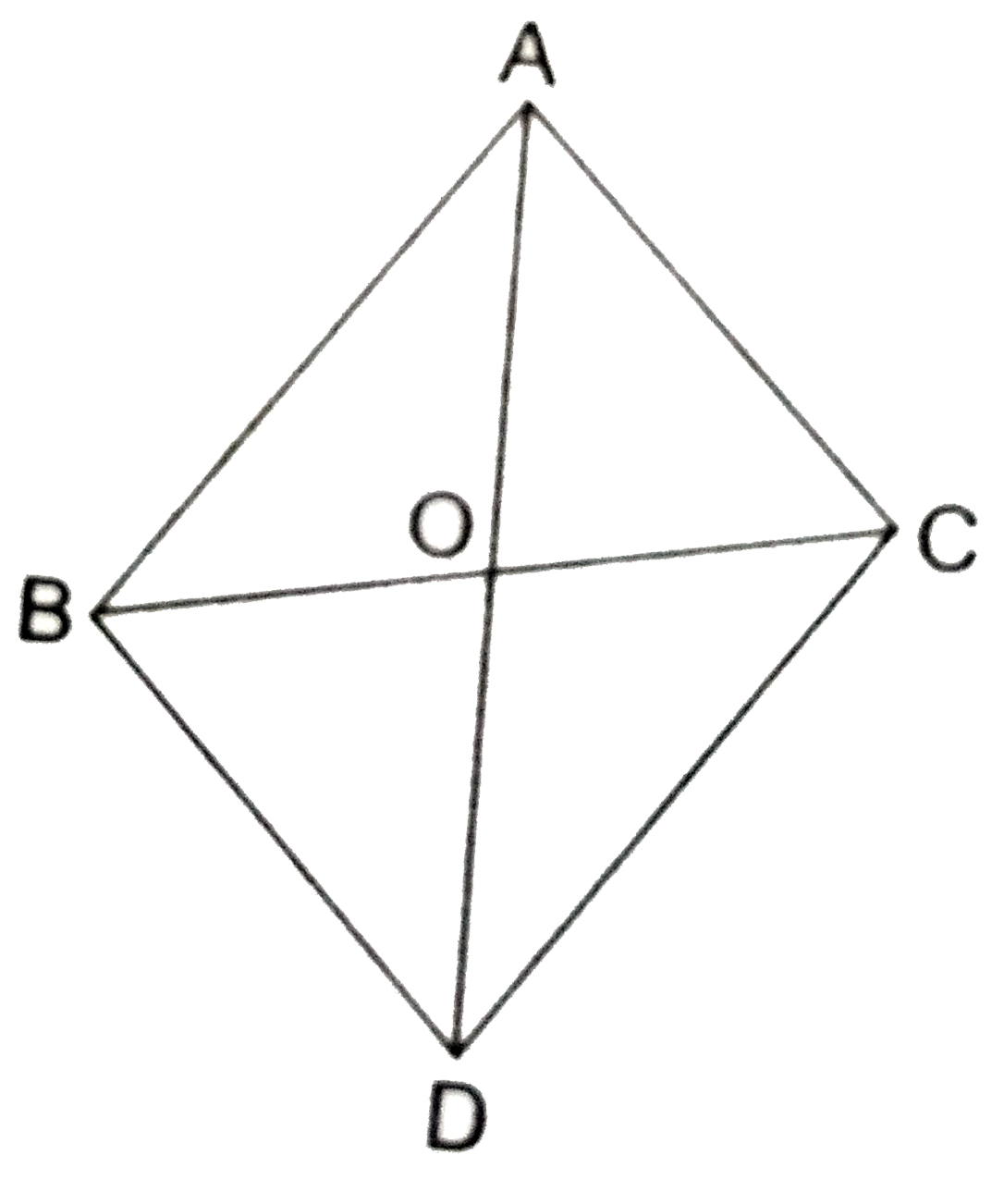
View Solution△ ABC and △ DBC are isosceles triangles on the same base BC. Prove that line AD bisects BC at right angles
View Solution