ΔABC is a right triangle right angled at A such that AB=AC and bisector of ∠C intersects the side AB at D. Prove that AC+AD=BC.
Video Solution
Text Solution
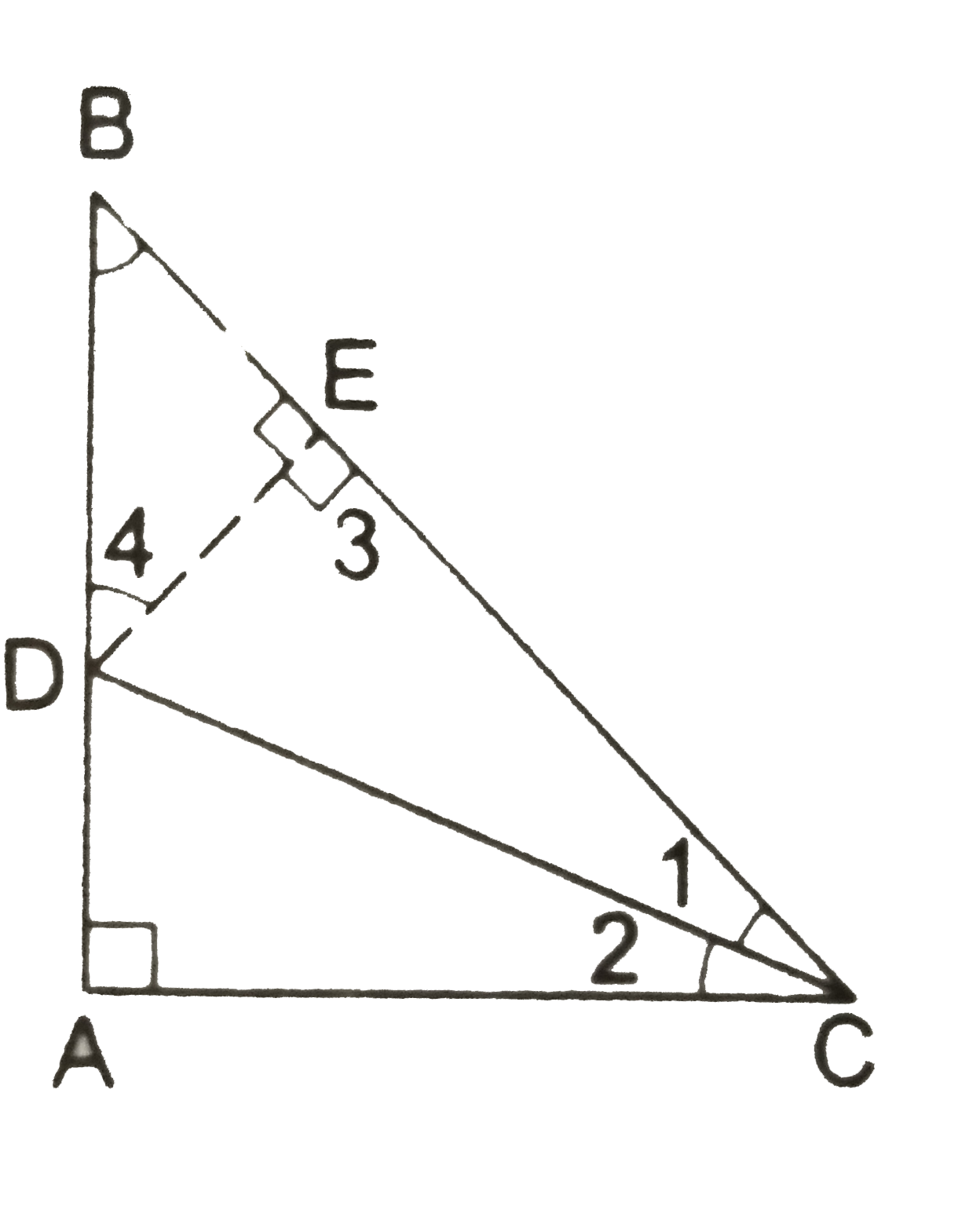
Given AΔABC in which AB=AC,∠A=90∘andCd bisect ∠C.
TO PROVE AC+AD=BC.
CONSTRUCTION Draw DE⊥BC.
PROOF ΔDAC≅ΔDEC as DC=DC,∠1=∠2,∠A=∠3=90∘.
∴ DA=DEandAC=EC.
Now, AB=AC⇒∠B=∠C.
∠A+∠B+∠C=180∘⇒90∘+∠B+∠B=180∘⇒∠B=45∘.
In ΔBED,∠4+∠B=90∘⇒∠4+45∘=90∘⇒∠4=45∘.
In ΔBDE,∠4=∠B⇒DE=BE⇒DA=DE=BE.
Now, BC=BE+EC=AD+AC.
|
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Exercise 9B
Explore 16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Multiple Choice Questions (Mcq)
Explore 20 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Multiple Choice Questions (Mcq)
Explore 20 Videos
- CIRCLES Book:RS AGGARWALChapter:CIRCLES Exercise:MULTIPLE CHOICE QUESTION(MCQ)
Explore 37 Videos
- COORDINATE GEOMETRYBook:RS AGGARWALChapter:COORDINATE GEOMETRYExercise:Multiple Choice Questions (Mcq)
Explore 22 Videos
Similar Questions
Knowledge Check
ΔABC is a right triangle , right angled at A and AD⊥BC . If AB= c and AC = b, then AD is equal to
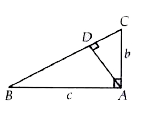 Abc√b2+c2Bbcb2+c2Cb2c√b2+c2DNone of these
Abc√b2+c2Bbcb2+c2Cb2c√b2+c2DNone of theseABC is a right-angled triangle, right angled at A and AD is the altitude on BC. If AB : AC= 3:4, what is the ratio BD:DC?
A3:4B9:16C2:3D1:2
ABC is an isosceles right triangle right-angled at C . Prove that AB2=2AC2 .
View SolutionΔABD is a right triangle, right-angled at A and AC⊥BD. Prove that AB2=BC×BD.
View SolutionABC is an isosceles right triangle, right-angled at C . Prove that: AB2=2AC2.
View SolutionABC is a isosceles right angled triangle, right angled at C. prove that AB2=2AC2
View SolutionABC is a triangle right angled at B. D is a point on AC such that ∠ABD=45∘ If AC=6 and AD=2 then AB=
View SolutionABC is a right triangle with AB = AC.If bisector of ∠A meet BC at D then prove that BC =2 AD .
View Solution