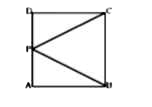
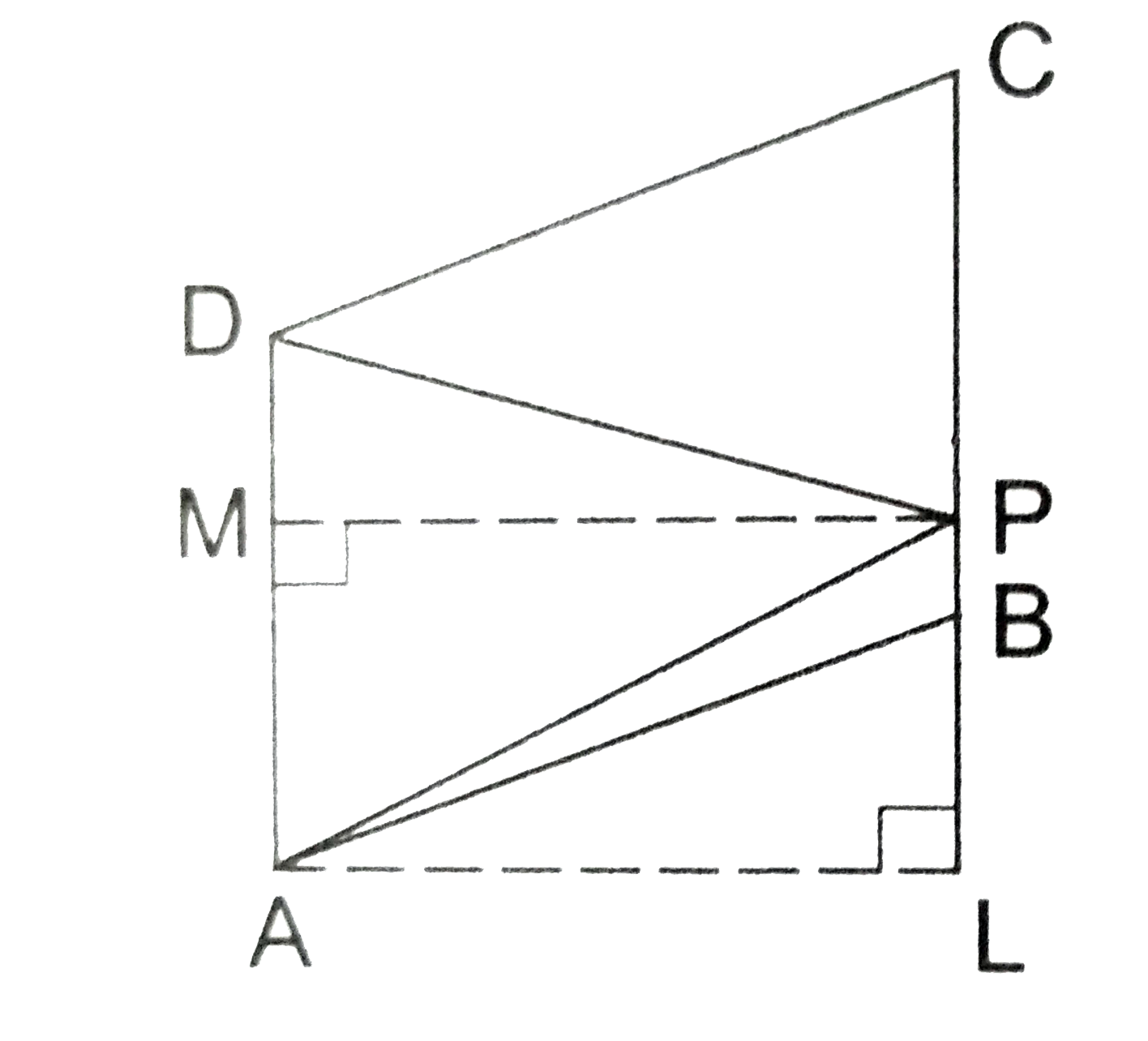
In the given figure, ABCD is a square and P is a point inside it such PB = Pd. Prove that CPA is a straight line.

Video Solution
Text Solution
ΔPAD≅ΔPAB⇒∠APD=∠APB.
ΔCPD≅ΔCPB⇒∠CPD=∠CPB.
∴ ∠APD+∠CPD=∠APB+∠CPB.
But, ∠APD+∠CPD+∠APB+∠CPB=360∘ [∠s around a point]
∴ ∠APD+∠CPD=180∘, i.e., CPA is a straight line.
ΔOBC≅ΔOAD as OB=OA,BC=AD,∠OBC=∠OAD=(90∘−60∘)=30∘.
Hence, OC=OD (c.p.c.t.).
|
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Exercise 9B
Explore 16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Multiple Choice Questions (Mcq)
Explore 20 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Multiple Choice Questions (Mcq)
Explore 20 Videos
- CIRCLES Book:RS AGGARWALChapter:CIRCLES Exercise:MULTIPLE CHOICE QUESTION(MCQ)
Explore 37 Videos
- COORDINATE GEOMETRYBook:RS AGGARWALChapter:COORDINATE GEOMETRYExercise:Multiple Choice Questions (Mcq)
Explore 22 Videos
Similar Questions
Knowledge Check
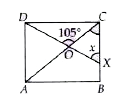
In the given figure, ABCD is a square. Find x.
 A60∘B120∘C100∘D110∘
A60∘B120∘C100∘D110∘In the given figure, ABCD is a square. The measure of ∠DBC is equal to
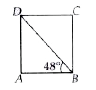 A48∘B38∘C42∘D52∘
A48∘B38∘C42∘D52∘In the given figure, ABCD is a square whose side is 4 cm. P is a point on the side AD. What is the minimum value (in cm) of BP+CP?
 A4√5B4√4C6√3D4√6
A4√5B4√4C6√3D4√6
In the given figure ABCD is a square . Find the measure of ∠CAD.

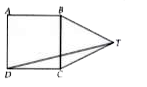
View SolutionIn the given figure, ABCD is a square and ΔBCT is an equilateral triangle. Find ∠BTD.
View SolutionIn the given figure, ABCD is a square whose side is 4 cm. P is a point on the side AD. What is the minimum value (in cm) of BP+CP?

View SolutionIn the adjoining figure, ABCD is a parallelogram and P is any points on BC. Prove that
ar(△ABP)+ar(△DPC)=ar(△PDA).
View SolutionIn the given figure PA=6, PB=4 and PC=8. Find PD.

View Solution