ABCD is a rhombus. If ∠ACB=30∘, then ∠ADB is
30∘
120∘
60∘
45∘
The correct Answer is:C
To solve the problem, we need to find the angle ∠ADB in the rhombus ABCD given that ∠ACB=30∘.
1. Understanding the Rhombus Properties:
- In a rhombus, opposite angles are equal, and adjacent angles are supplementary (i.e., they add up to 180∘).
- The diagonals of a rhombus bisect each other at right angles.
2. Identifying Angles:
- We are given ∠ACB=30∘.
- Since ABCD is a rhombus, AC and BD are the diagonals.
3. Finding ∠ACD:
- Since AC and BD bisect each other at right angles, ∠ACD will also be 30∘ because ∠ACB and ∠ACD are alternate interior angles formed by the transversal AC with the parallel lines AB and CD.
4. Using the Triangle Sum Property:
- In triangle ACD, we know:
∠DAC+∠ACD+∠ADB=180∘
- We know ∠ACD=30∘ and ∠DAC=90∘ (since diagonals bisect each other at right angles).
5. Calculating ∠ADB:
- Substitute the known angles into the triangle sum equation:
90∘+30∘+∠ADB=180∘
- Simplifying gives:
∠ADB=180∘−120∘=60∘
Final Answer:
Thus, ∠ADB=60∘.
---
- In a rhombus, opposite angles are equal, and adjacent angles are supplementary (i.e., they add up to 180∘).
- The diagonals of a rhombus bisect each other at right angles.
- We are given ∠ACB=30∘.
- Since ABCD is a rhombus, AC and BD are the diagonals.
- Since AC and BD bisect each other at right angles, ∠ACD will also be 30∘ because ∠ACB and ∠ACD are alternate interior angles formed by the transversal AC with the parallel lines AB and CD.
- In triangle ACD, we know:
∠DAC+∠ACD+∠ADB=180∘
- We know ∠ACD=30∘ and ∠DAC=90∘ (since diagonals bisect each other at right angles).
- Substitute the known angles into the triangle sum equation:
90∘+30∘+∠ADB=180∘
- Simplifying gives:
∠ADB=180∘−120∘=60∘
Thus, ∠ADB=60∘.
Similar Questions
Knowledge Check
In the given figure, ABCD is a rhombus. If ∠A=70∘, then ∠CDB is equal to
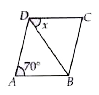 A65∘B55∘C75∘D80∘
A65∘B55∘C75∘D80∘ABCD is a rhombus such that ∠ACB=40∘, then ∠ADB is
A40∘B45∘C50∘D60∘If ABCD is a rhombus, then
AAC2+BD2=6AB2BAC2+BD2=5AB2CAC2+BD2=4AB2DAC2+BD2=3AB2
In a rhombus ABCD if ∠ACB=40∘, then fine ∠ADC.
View SolutionABCD is a rhombus. ∠DAB=2x+15∘,angle DCB =3x−30∘, angle BDC equals
View SolutionIn the adjoining figure ABCD is a rhombus. If ∠A=70∘ then ∠CDB=?
View SolutionIf ABCD is a rhombus, then
View SolutionABCD is a rhombus in which ∠C=60∘then AC:BD=.
View Solution

