ABCD is a rhombus such that ∠ACB=40∘, then ∠ADB is
A
40∘
B
45∘
C
50∘
D
60∘
Video Solution
Text Solution
The correct Answer is:C
Given, ABCD is a rhombus such that ∠ACB=40∘⇒∠OCB=40∘
Since, AD∣∣BC
∠DAC=∠BCA=40∘ [alternate interior angles]
Also, ∠AOD=90∘
[diagonals of a rhombus are perpendicular to each other]
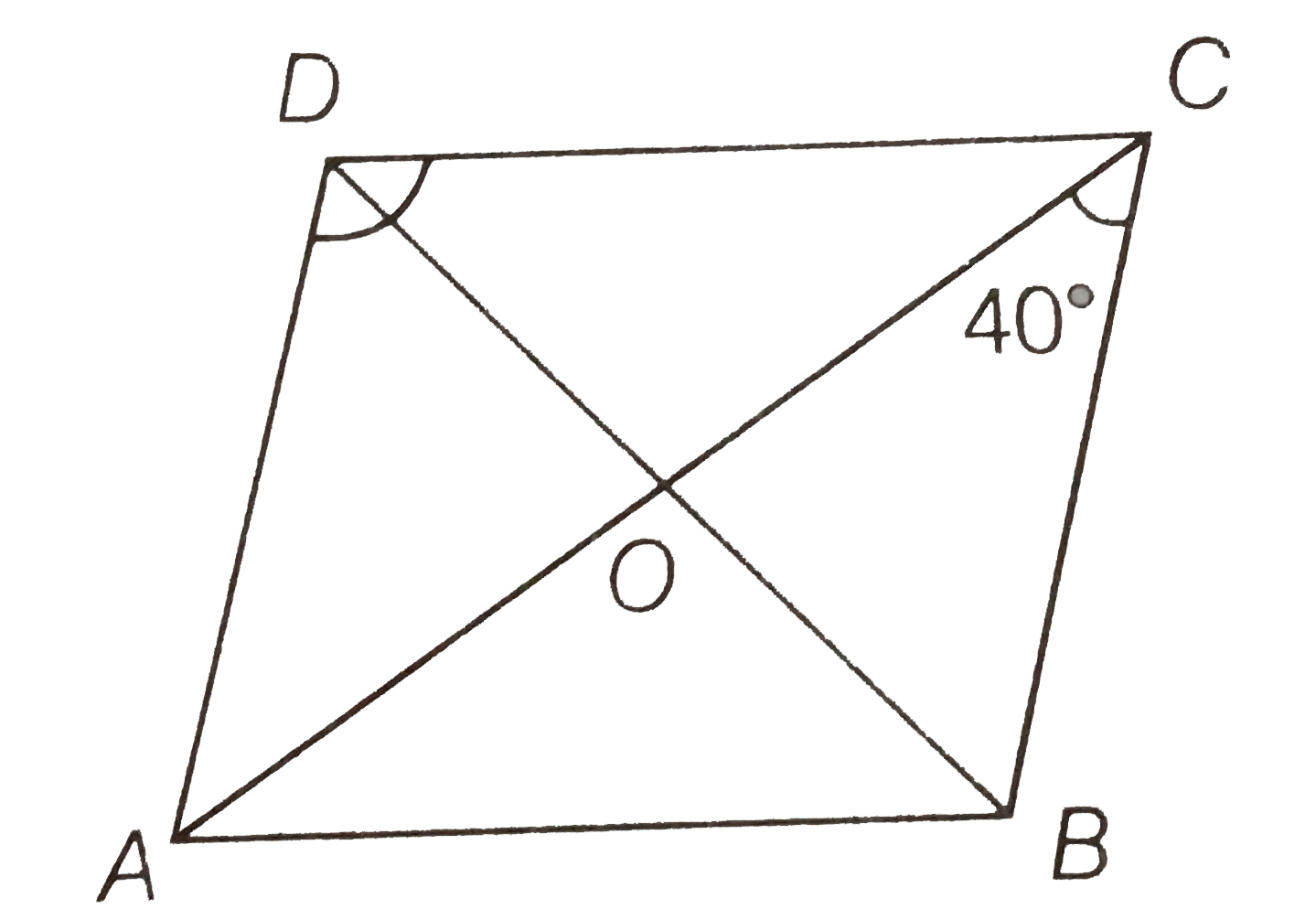
We know that, sum of all angles of a triangle ADO is 180∘.
∴∠ADO+∠DOA+∠OAD=180∘
∴ ∠ADO=180∘−(40∘+90∘)
=180∘−130∘=50∘
⇒ ∠ADB=50∘
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
ABCD is a rhombus such that ∠ACB=40∘. Find ∠ADB.
A20∘B30∘C50∘D40∘ABCD is a rhombus such that ∠ACB=50∘. Then. ∠ADB= ?
A50∘B40∘C65∘D130∘If ABCD is a rhombus, then
AAC2+BD2=6AB2BAC2+BD2=5AB2CAC2+BD2=4AB2DAC2+BD2=3AB2
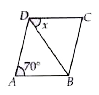
In the given figure, ABCD is a rhombus. If ∠A=70∘, then ∠CDB is equal to
View SolutionIf ABCD is a rhombus, then :
View SolutionIf ABCD is a rhombus, then :
View SolutionABCD is a rhombus in which ∠C=60∘then AC:BD=.
View SolutionABCD is rhombus and ∠BAD=60∘. The measure of ∠CAB is _______
View Solution

