In a circulat table cover of radius 42 cm, a design is formed, leaving an equilateral triangle ABC in the middle as shown in the figure.
Find the area of the design. [ Use √3=1.73]
![In a circulat table cover of radius 42 cm, a design is formed, leaving an equilateral triangle ABC in the middle as shown in the figure. Find the area of the design. [ Use sqrt(3)=1.73]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RSA_MATH_X_C16_S01_032_Q01.png)
The correct Answer is:1888.11 cm2
Step by step video, text & image solution for In a circulat table cover of radius 42 cm, a design is formed, leaving an equilateral triangle ABC in the middle as shown in the figure. Find the area of the design. [ Use sqrt(3)=1.73] by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. 12.24. Find the area of the design (shaded region).

View SolutionIn a circular table cover of radius 32 cm, a design (shade) is formed leaving an equilateral traingle ABC in the middle as shown in the adjacent figure.Find the area of the shaded region.
View Solution
Knowledge Check
The area of an equilateral triangle with side 2√3 cm is
A5.196 cm2B0.866 cm2C3.496 cm2D1.732 cm2In an equilaterial triangle of side 2√3 cms, the circum-radius ,is
A1cmB√3cmC2cmD2√3cm
In a circular table cover of radius 32cm, a design is formed leaving an equilateral triangle ABC as shown in figure. Find the area of shaded region.
View SolutionA girl formed of design in a circle of radius 42 cm leaving an equilateral triangle ABC in the middle as shown in the figure. Find the corvered area of the design. (Use √3=1.73andπ=227)

View SolutionConsider an equilateral triangle of side √6 as shown in figure. Find the area of the shaded region
View SolutionIf arcs of radius r cm are drawn with the vertices of an equilateral triangle ABC as shown in the figure, then the area of the shaded region is
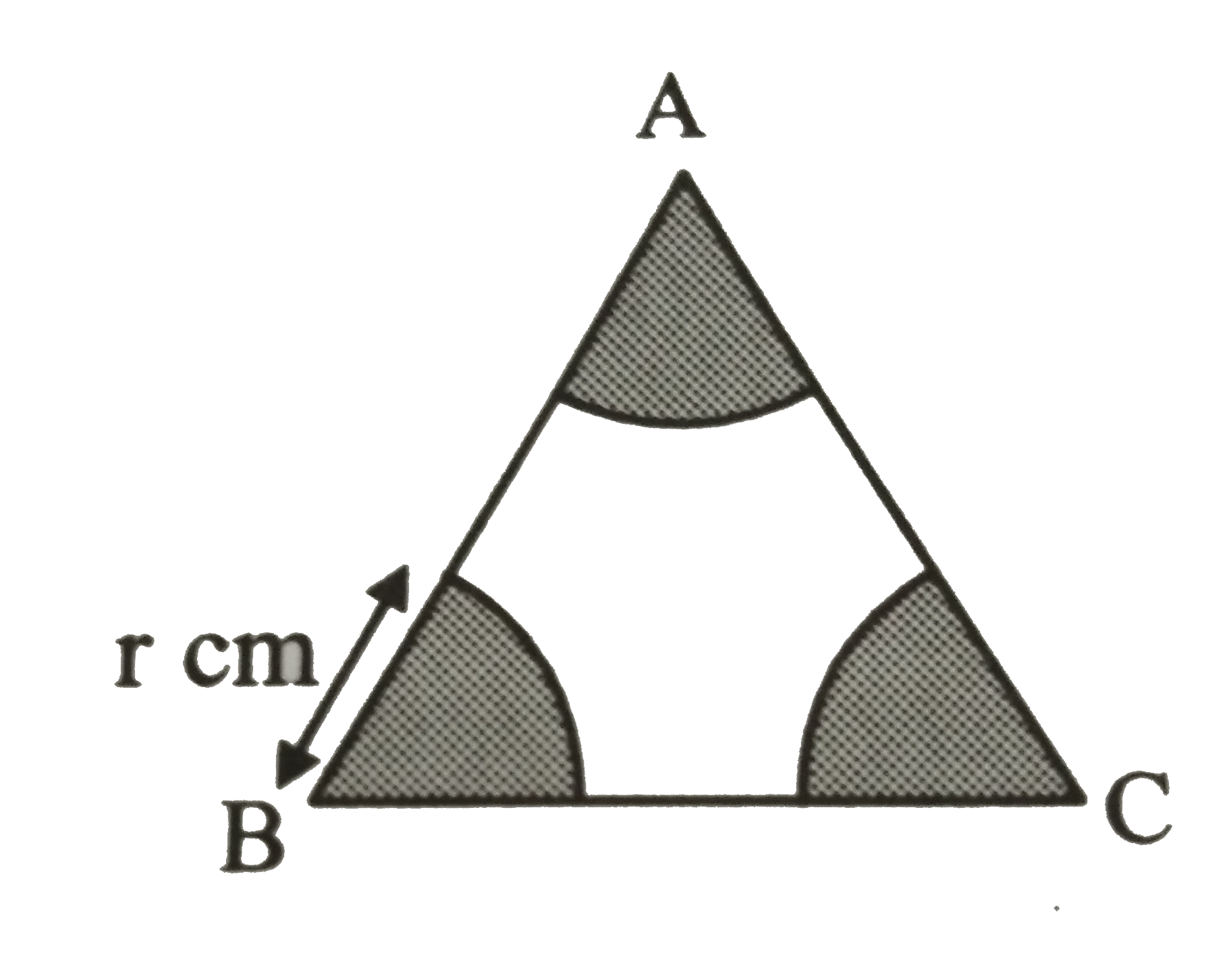
View SolutionABC is an equilateral triangle inscribed in a circle of radius 4 cm. Find the area of the shaded portion.

View SolutionIn the given figure, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region. [Use √3=1.73 and π=3.14]
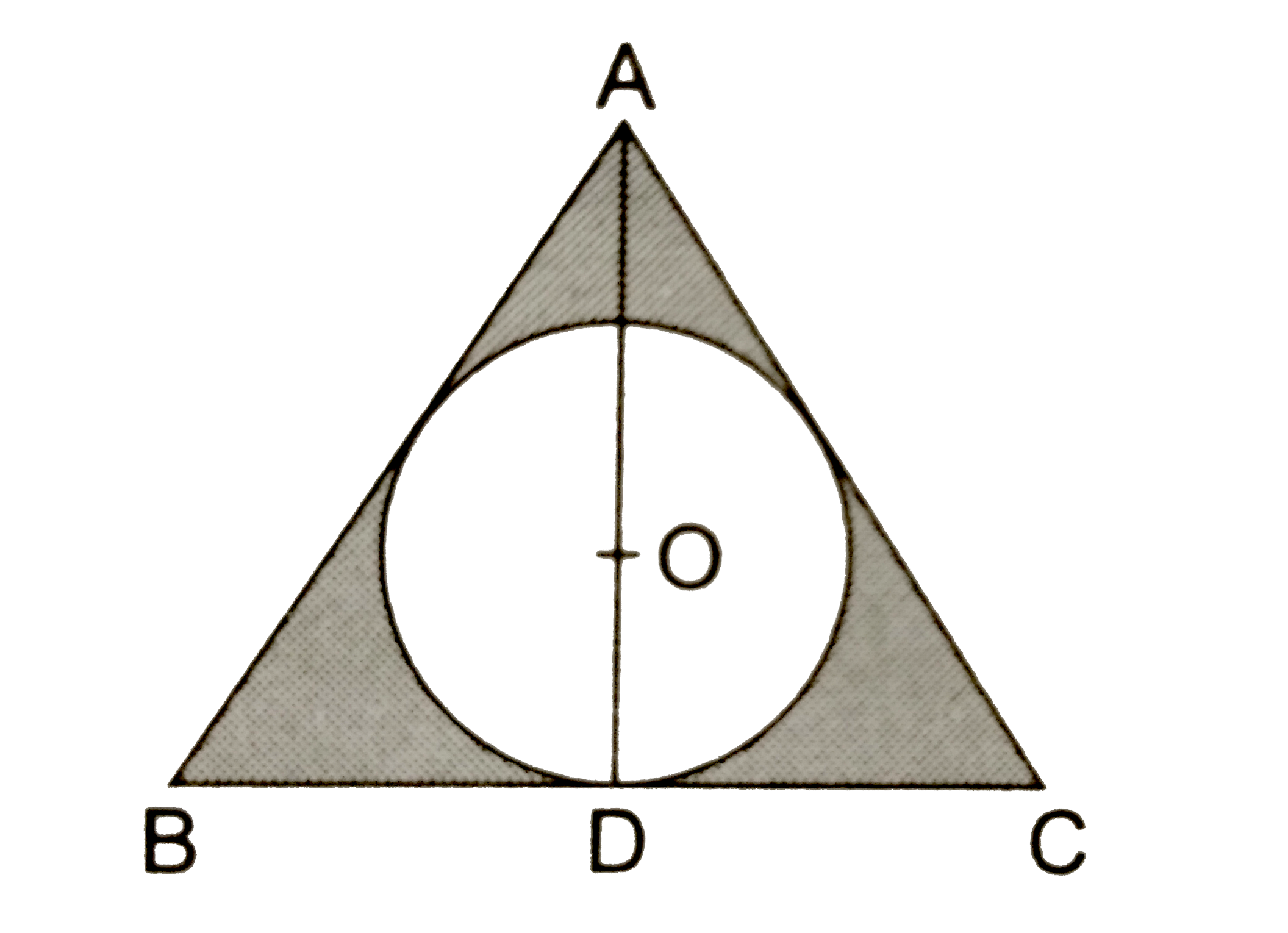
View Solution
