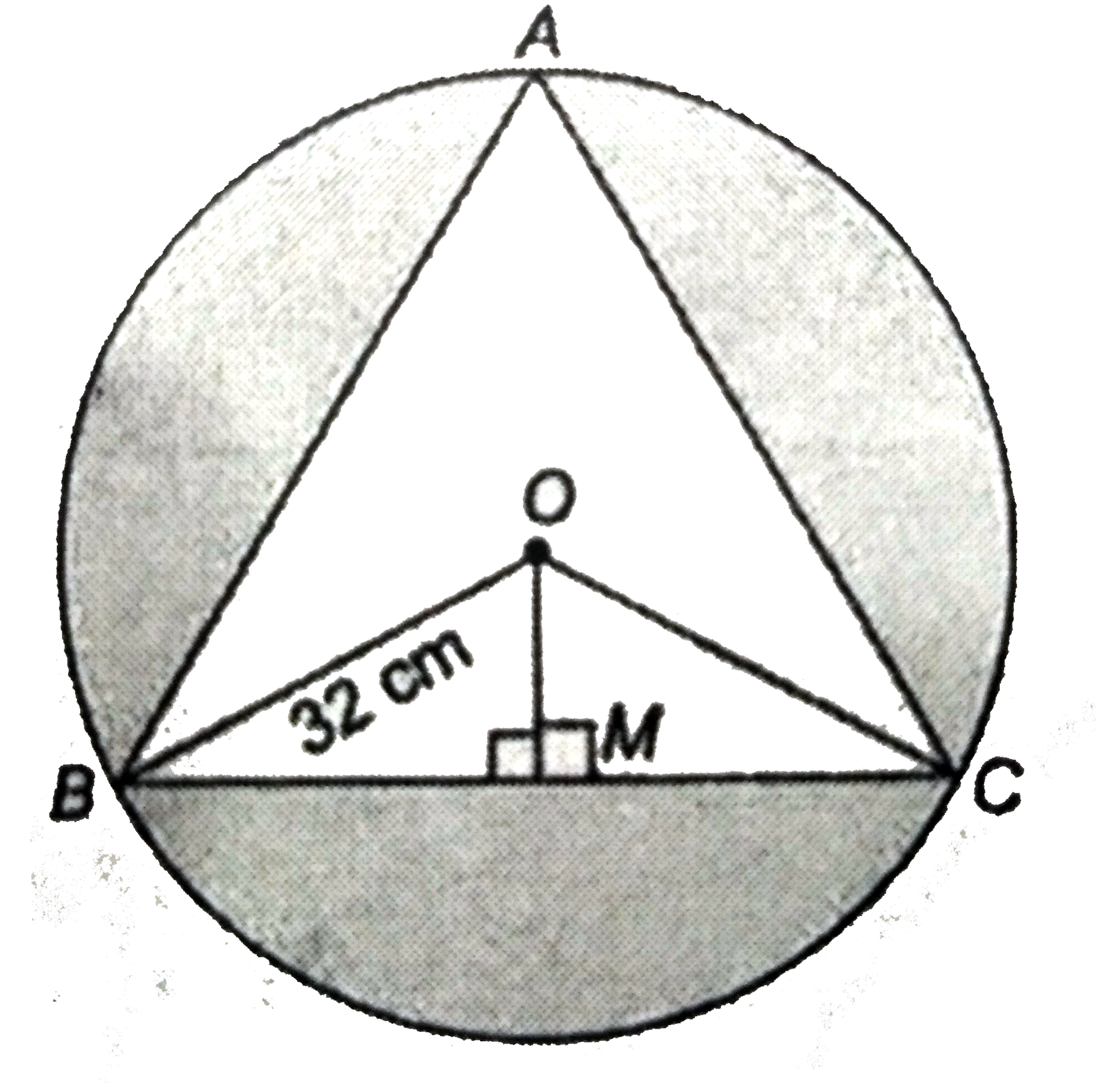
In a circular table cover of radius 32 cm, a design (shade) is formed leaving an equilateral traingle ABC in the middle as shown in the adjacent figure.Find the area of the shaded region.
Since ABC is an equilateral triangle.
∴Ang≤A=60∘
⇒∠BOC=2×∠BAC=2×60∘=120∘
(degree measure of an arc is twice the angle subtended by it in alternate segment)
Draw OM⊥BC
So, we can prove
ΔOMB≅ΔOMC (R.H.S. congruency)
∴∠BOM=∠COM=60∘ (c.p.c.t)
In right ΔOMB, we have
sin60∘=BMOB
⇒√32=BM32⇒BM=16√3cm
∴BC=2×16√3=32√3cm
∴ Area of shaded region = Area of circle −ar(ΔABC)
=πr2−(side)2√34=π×(32)2−(32√3)2×√34
=(32)2(227−3√34)=1024(227−3√34)cm2
Topper's Solved these Questions
- AREA RELATED TO CIRCLESBook:NAGEEN PRAKASHANChapter:AREA RELATED TO CIRCLESExercise:Problems From NCERT /exemplar
Explore 25 Videos
- AREA RELATED TO CIRCLESBook:NAGEEN PRAKASHANChapter:AREA RELATED TO CIRCLESExercise:Exercise 12 A
Explore 25 Videos
- ARITHMETIC PROGRESSIONBook:NAGEEN PRAKASHANChapter:ARITHMETIC PROGRESSIONExercise:Revision Exercise Long Answer Question
Explore 5 Videos
Similar Questions
In figure , find the area of the shaded region
View SolutionIn a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. 12.24. Find the area of the design (shaded region).

View SolutionIn a circulat table cover of radius 42 cm, a design is formed, leaving an equilateral triangle ABC in the middle as shown in the figure.
Find the area of the design. [ Use √3=1.73]

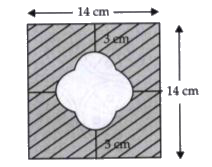
View SolutionIn the following figures, find the area of the shaded region.
View SolutionIn a circular table cover of radius 32cm, a design is formed leaving an equilateral triangle ABC as shown in figure. Find the area of shaded region.
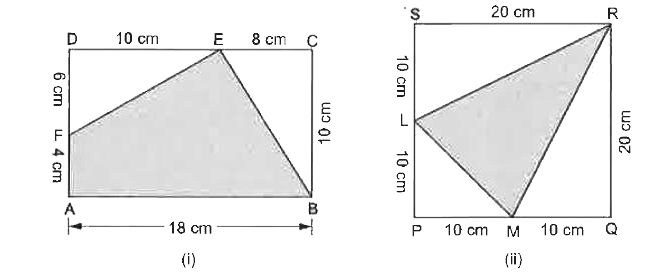
View SolutionFind the area of the shaded region in Figure.
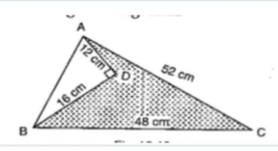
View SolutionFind the area of the shaded region in figure.

View SolutionFind the area of the shaded region in figure .
View SolutionConsider an equilateral triangle of side √6 as shown in figure. Find the area of the shaded region
View SolutionIn figure, find the area of the shaded region [Useπ=3.14]
View Solution
