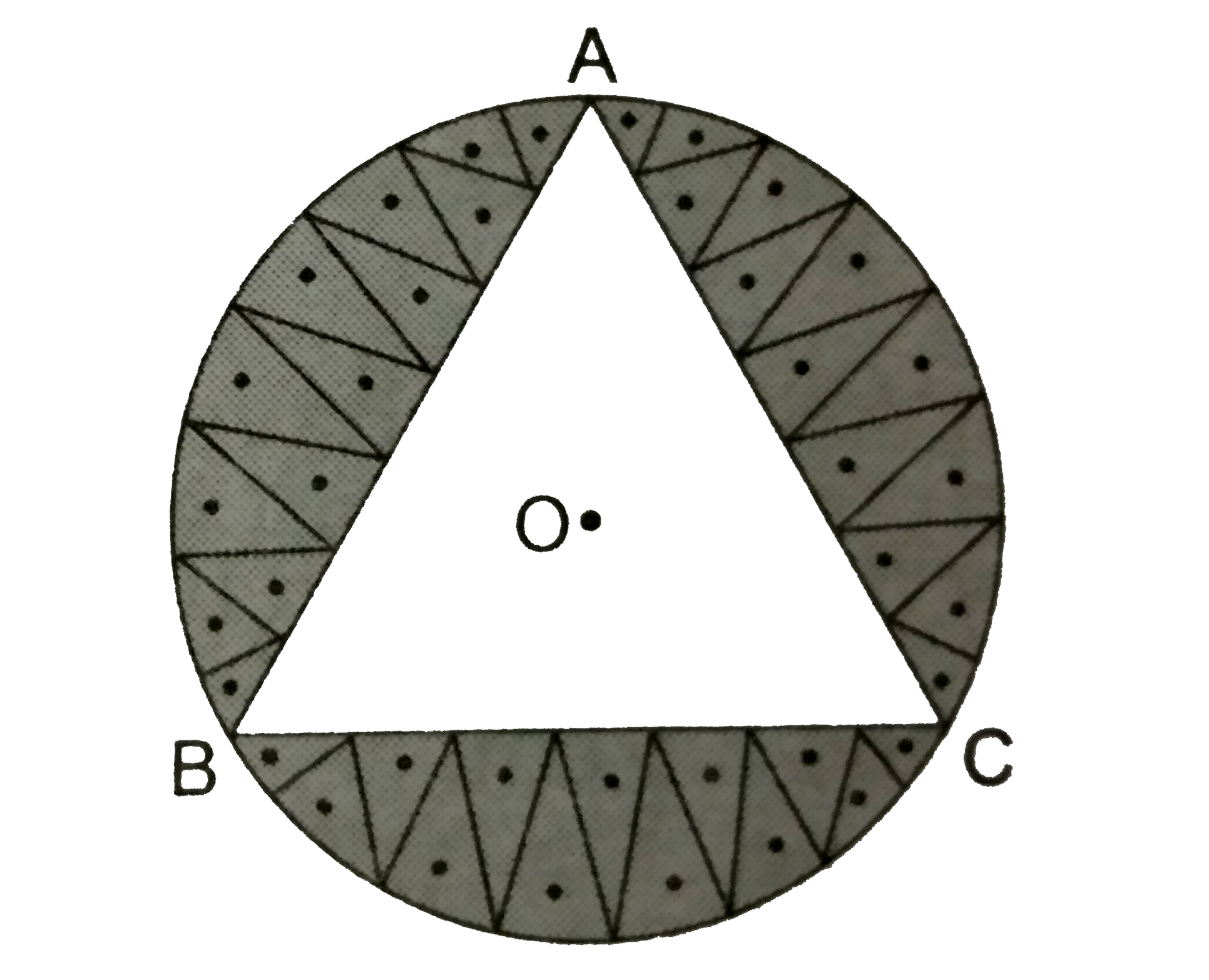
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. 12.24. Find the area of the design (shaded region).
In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. 12.24. Find the area of the design (shaded region).

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

We use the concept of areas of circle and equilateral triangle in the problem.
Mark O as center of the circle. Join BO and CO.
Since we know that equal chords of a circle subtend equal angles at the center and all sides of an equilateral triangle are equal,
Each side of △ABC will subtend equal angles at the center.
∠BOC=360∘3=120∘
Consider △BOC. Drop a perpendicular from OM to BC
We know perpendicular from the center of circle to a chord bisects it.
BM=MC
OB=OC (radii)
OM=OM (common)
△OBM≅△OCM (by SSS congruency)
∠BOM=∠COM (by CPCT)
2∠BOM=∠BOC=120∘
∠BOM=120∘2=60∘
sin60∘=BMBO=√32
BM=√32×BO=√32×32=16√3
BC=2BM=32√3
Using the formula of area of equilateral triangle = √34(side)2
We can find the area of △ABC since a side BC of △ABC is known.
Visually from the figure, it’s clear that
Area of the design = Area of circle - Area of △ABC = πr2−√34(BC)2
This can be solved with ease as both the radius of the circle and BC are known.
Radius of circle (r) = 32cm
From figure, we observe area of design = Area of circle - Area of △ABC
= πr2−√34(BC)2
= 227×(32)2−√34×(32√3)2
= 227×1024−√34×1024×3
= 225287−768√3
Area of design = (225287−768√3)cm²

Updated on:21/07/2023
|
Class 10MATHSAREA RELATED TO CIRCLE

Topper's Solved these Questions

Similar Questions