In Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
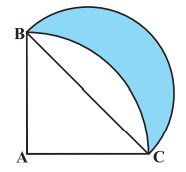
To find the area of semi-circle, we need to find the radius or diameter (BC) of the semicircle.
△ABC is a right-angled triangle, right-angled at A (ABC being a quadrant).
AB=AC=14cm [Radius of the circle]
Using Pythagoras theorem, we can find the hypotenuse (BC) of △ABC.
BC2=AB2+AC2
= (14cm)2+(14cm)2
BC = (√2)×(14cm)2
= 14√2cm
Radius of semicircle BDC, r=BC2=14√22cm=7√2cm
Area of the shaded region = Area of semicircle - (Area of quadrant ABC - Area △ABC)
= πr22−[90∘360∘×π(14)2−12×AC×AB]
= (π(7√2))22−[(π(14))24−12×14×14]
= [22×7×7×27×2]−[22×14×147×4−7×14]
= 154−(154−98)
= 98cm2
Topper's Solved these Questions
- AREAS RELATED TO CIRCLESBOOK - NCERTCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - EXERCISE 12.1
5 Videos
- AREAS RELATED TO CIRCLESBOOK - NCERTCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - SOLVED EXAMPLES
6 Videos
- AREAS RELATED TO CIRCLESBOOK - NCERTCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - SOLVED EXAMPLES
6 Videos
- ARITHMETIC PROGRESSIONSBOOK - NCERTCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Exercise 5.3
20 Videos
Similar Questions
In Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.

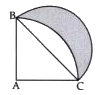
View SolutionIn the given figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
View Solution
Knowledge Check
In the adjoining figure, ABCD is a square of side 7 cm and two semicircles are drawn inside of it with AB and CD as diameters. Find the area of the shaded region (in cm2).
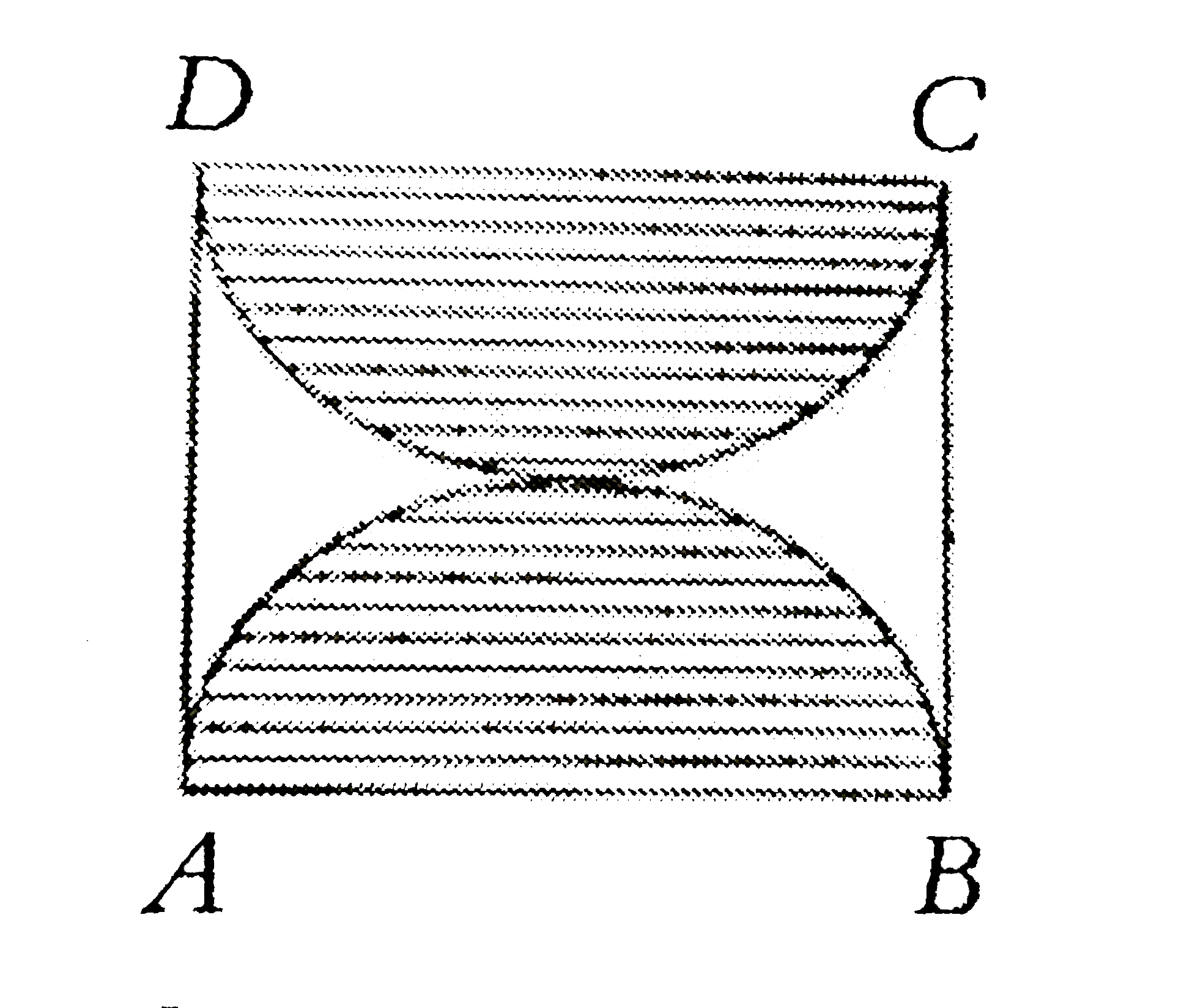 A144 m2B164 m2C184 m2D154 m2
A144 m2B164 m2C184 m2D154 m2
In the given figue, ABCD is a quadrant of a circle of radius 28 cm and a semicircle ABECA is drawn with AC as diameter. Find the area of the shaded region.
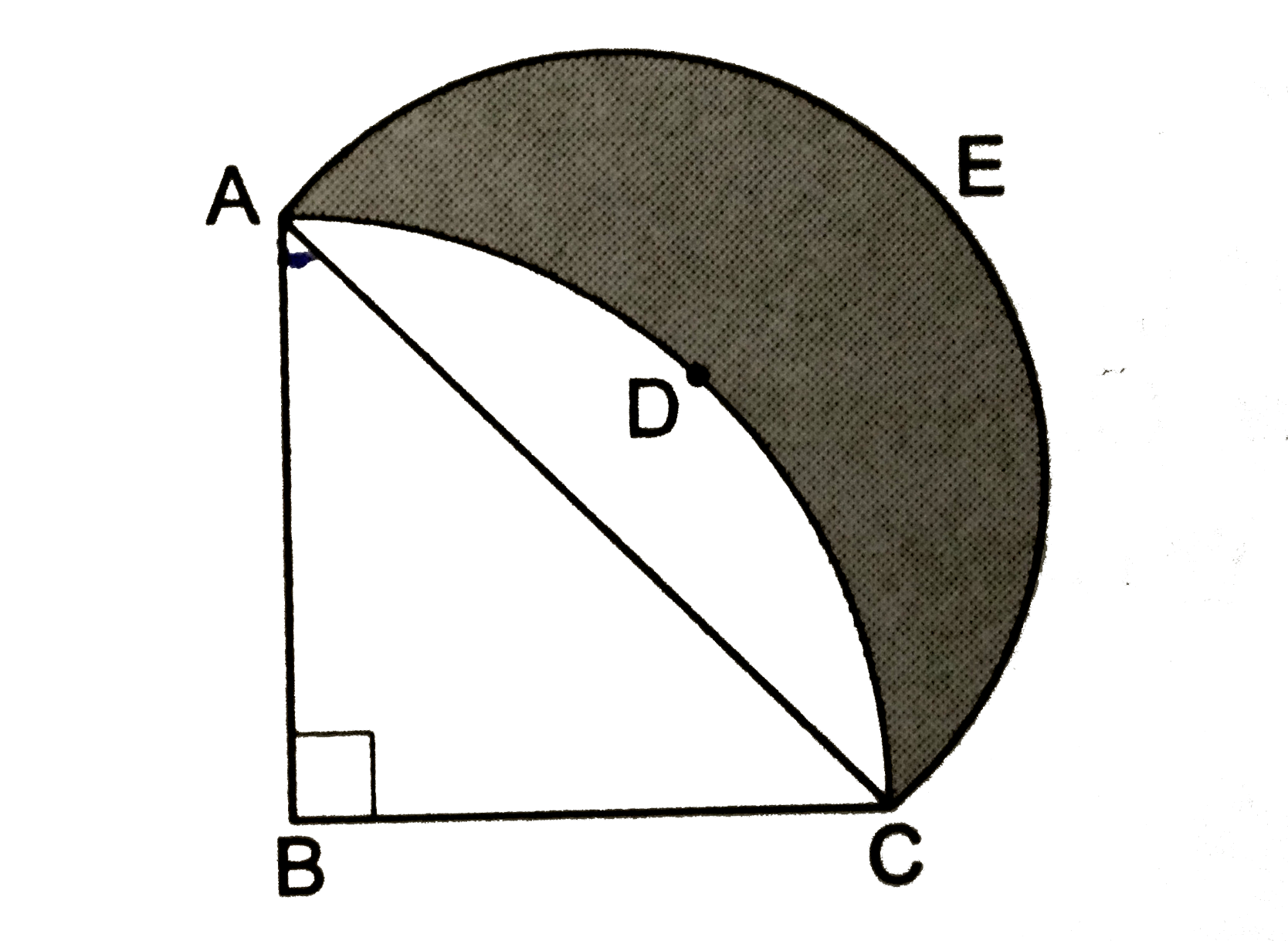
View SolutionIn figure ABDC is a quadrant of a circle of a radius 28 cm and a semi circles BEC is drawn with BC as diameter find the area of shaded region:
View SolutionABCP is a quadrant of a circle of radius 14 cm. with AC as diameter, a semicircle is drawn. Find the area of the shaded portion
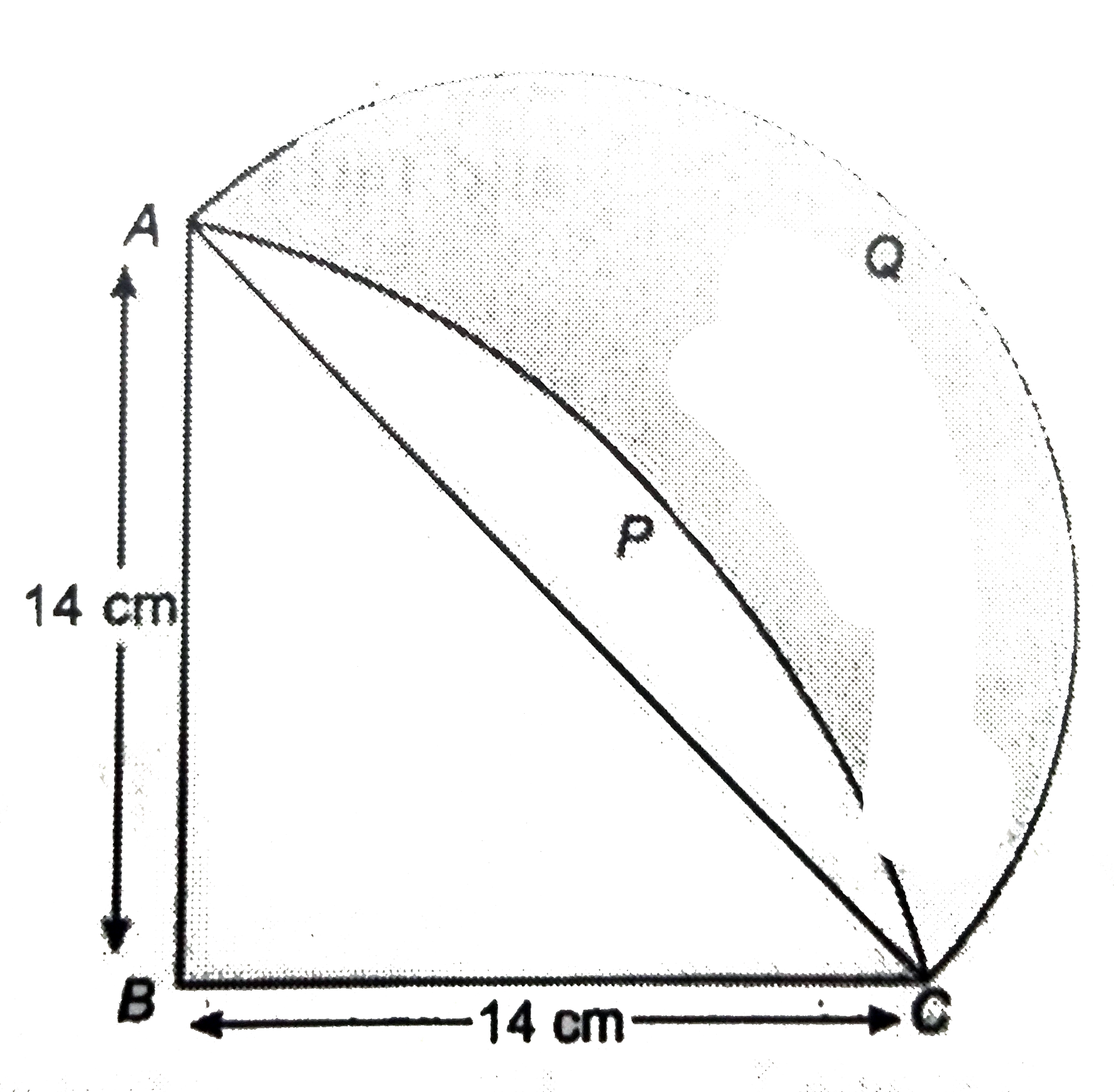
View SolutionBCP is a quadrant of a circle of radius 14cm. With AC as diameter, a semi-circle is drawn. Find the area of the shaded portion.
View SolutionABCP is a quadrant of a circle of radius 14 cm. With AC as diameter, a semi-circle is drawn. Find the area of the shaded portion.
View SolutionIn Fig. 12.64, ABCP is a quadrant of a circle of radius 20 cm. With AC as diameter, a semi-cirde is drawn. Find the area of the shaded portion.

View SolutionIn the given figure, ABCD is a square of side 10 cm and semicircles are drawn with each side of the square as diameter. Find the area of the shaded region.
[ Use π=3.14]

View Solution
