A cylinder of mass m is suspended through two strings wrapped around it as shwon in figure . Find a. the tension T in the string and b. the speed o the cylinder as it falls through a distance h.
 Solution in Gujrati
Solution in Gujrati
The portion of th strings between the cweiling and the cylinder is at rest. Hence the oints o the cuylinder where the strings leave it are at rest. The cylinder is thus rolling withuot sliping on the strings. Suppose the centre of the cylinder falls with n acceleration a. The ngular acceleration of he cylenere about its axis s α=aR, as the cylinder does not slip ovr teh strings.
The equation of motion for the centre of mass of the cylinder is
mg-2T=ma.............i<br>andforthemotionaboutthecentreofmassitas<br>2Tr=(1/2mr^2alpha)=1/2mra<br>or2T=1/2ma............ii<br>Fromiandii<br>a=2/3g and T=(mg)/6<br>Asthecentreofthecyl∈der⋆tsmov∈gomrest,tehvelocityafterithsfal≤nthroughadistancehisgivenby<br>v^2=2(2/3g)h<br>orv=(sqrt(4gh))/3
Similar Questions
A string is wrapped around a cylinder of mass M and radius r. The string is pulled vertically upward to prevent the center of mass from falling as the cylinder unwinds the string. (a) What is the tension in the string? B) How much work has been done on the cylinder once it has reached an angular speed omega ? c) what is the length of string unwound in the time its acquires angular speed omega ?
View SolutionA string is wrapped around a cylinder of mass M and radius R(=2√2m).The string is pulled vertically upward to prevent the centre of mass from falling as the cylinder unwinds the string.Find the length of the string unwound when the cylinder has reached a speed ω(=5rad/s).(g=10ms2)
View SolutionA cylinder of mass m is suspended through two strings wrapped around it as shwon in figure . Find a. the tension T in the string and b. the speed o the cylinder as it falls through a distance h.

View SolutionA solid cylinder of mass M and radius .R. is mounted on a frictionless horizontal axle so that it can freely rotate about this axis. A string of negligible mass is wrapped round the cylinder and a body of mass .m. is hung from the string. The mass is released from rest. Find the tension in the string and the angular speed of cylinder as the mass falls a distance h.
View SolutionA cylinder of mass M and radius R starts falling under gravity at t = 0 as shown in figure. If the mass of chord is negligible, the tension in each string is:
View SolutionA massless string is wrapped around a uniform solid cylinder of mass 30kg and radius 0.20m. One end of the string is attahed to the cylinder and the free end is pulled tangentially by a force that maintains a constant tension of 3.0 N. Find a) the angular acceleration and b) The angular speed of the cylinder 2.0 s after the force is applied to the cylinder at rest.
View SolutionConsider the arrangement shown in figure. The string is wrapped around a uniform cylinder which rolls without slipping. The other end of the string is passed over a masslessm frictionless pulley to a falling weight, determine the acceleration of the falling mass m in terms of only the mass of the cylinder M , the mass m and g
View Solution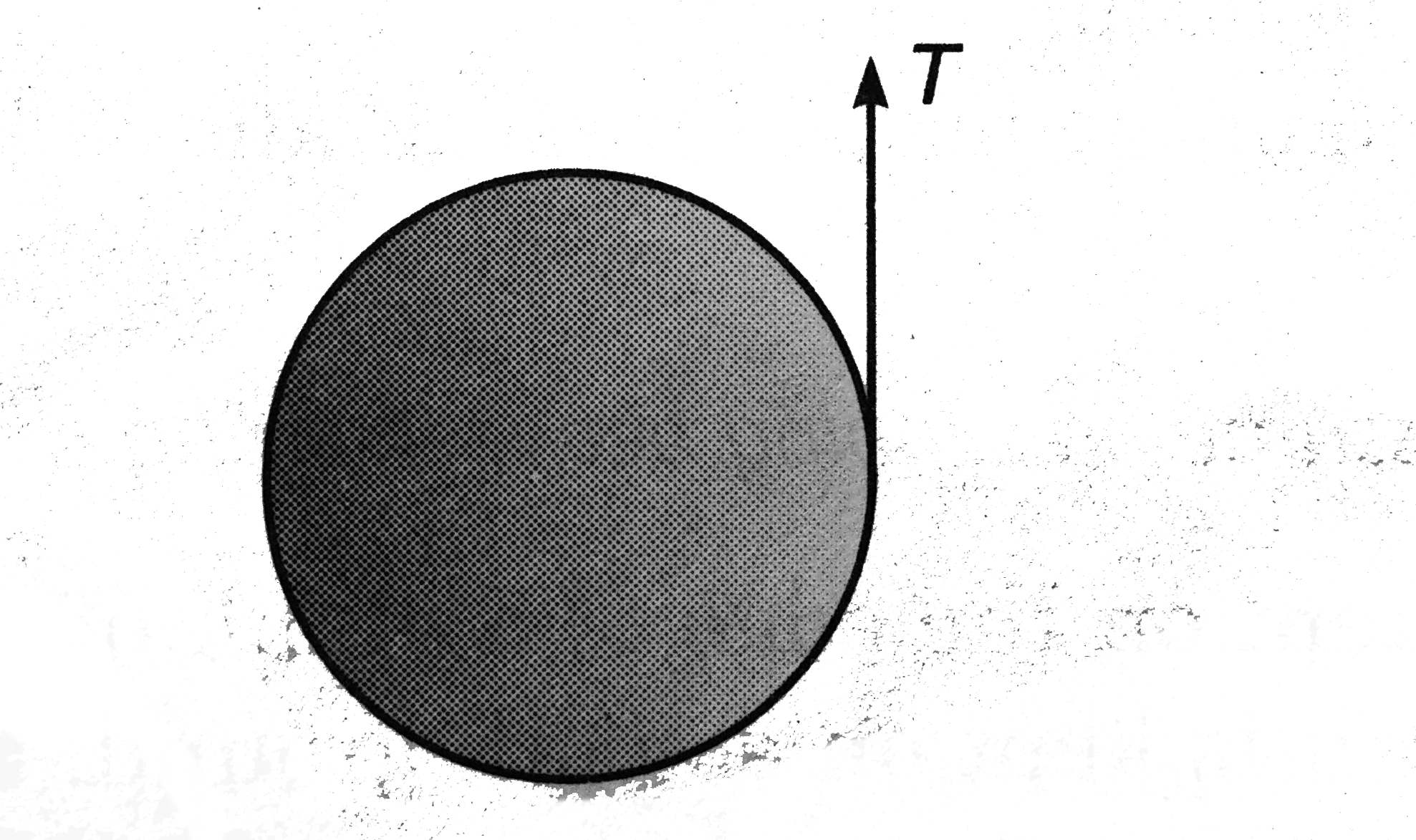
A uniform cylider of mass M and radius R has a string wrapped around it. The string is held fixed and the cylinder falls vertically, as in figure.
(a). Show that the acceleration of the cylinder is downward with magnitude a=2g3
(b). Find the tension in the string.
View Solution
