A solid cylinder has a thin string wrapped several times around its circumference. The string is fixed at one end and the cylinder is released. Find the downward acceleration of cylinder and tension in the string.
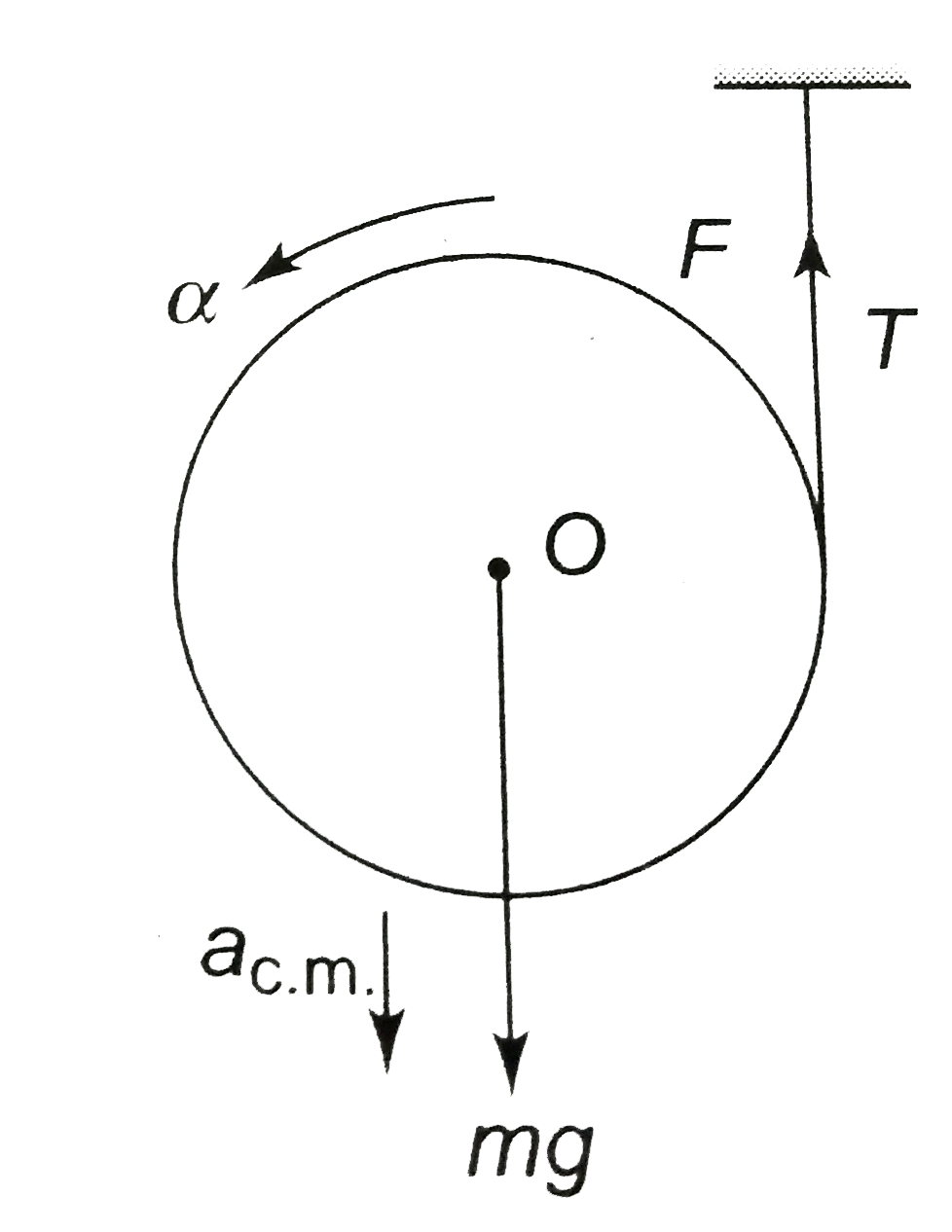
()
()
()
()
From (), () and ()
OR
The body rolls without slipping on vertical surface
Topper's Solved these Questions
Similar Questions
A disc of mass M has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the ceiling and the disc is released from rest. Find the acceleration of the disc and the tension in the string.
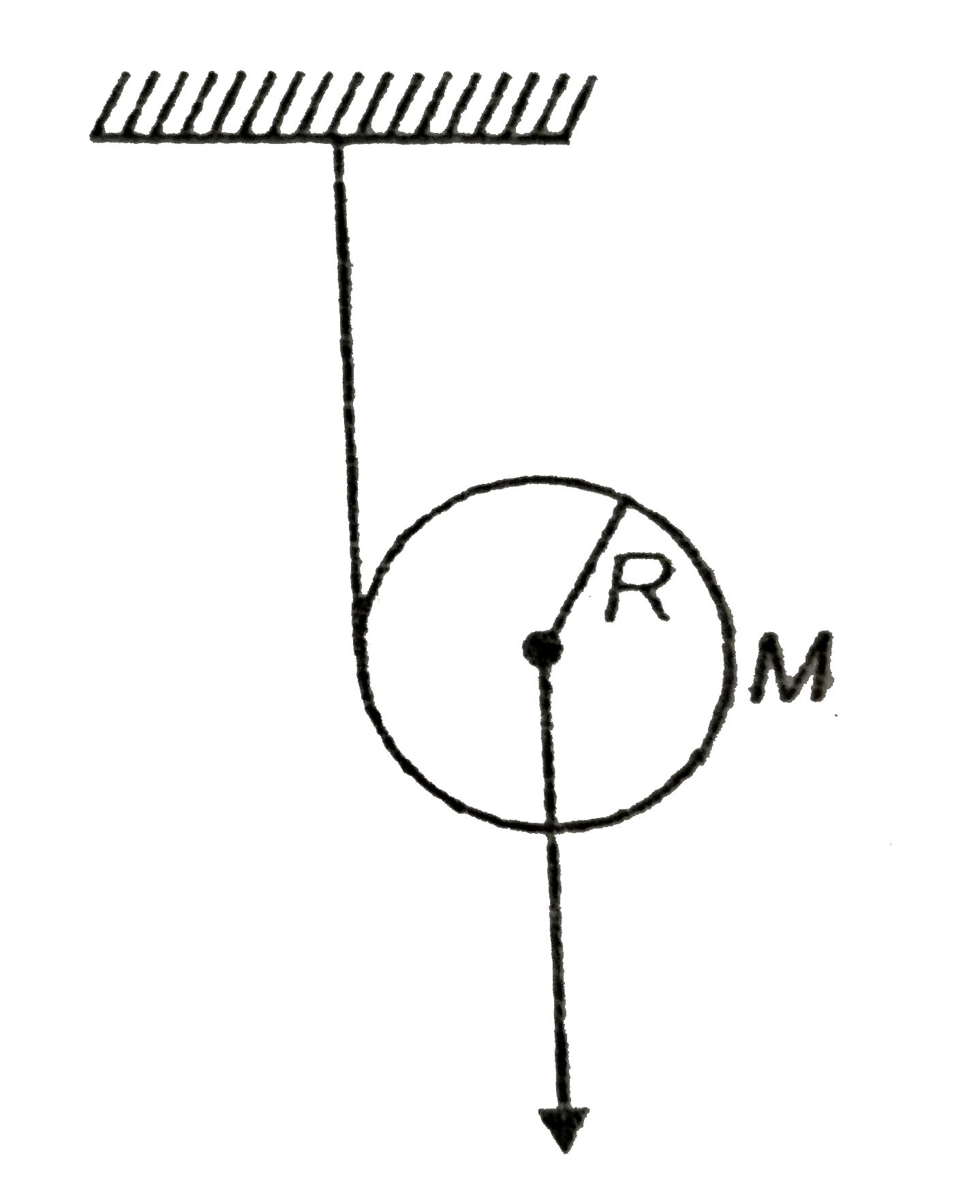
View SolutionA uniform round object of mass M, radius R and moment of inertia about its centre of mass Icm has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the celling and the object is released from rest. Find the acceleration of centre of the object and tension n the string. [ Take IcmMR2=k]
View Solution
Knowledge Check
A string is wrapped several times round a solid cylinder. Then free end of the string is held stationary. If the cylinder is released to move down, then the acceleration of that cylinder is
Ag/3Bg/2C3g/2D2g/3A uniform cylinder free to turn around a fixed axis has a string wrapped around it as shown. The string is pulled with a force F equal to the cylinders weight. What is the acceleration of the string?
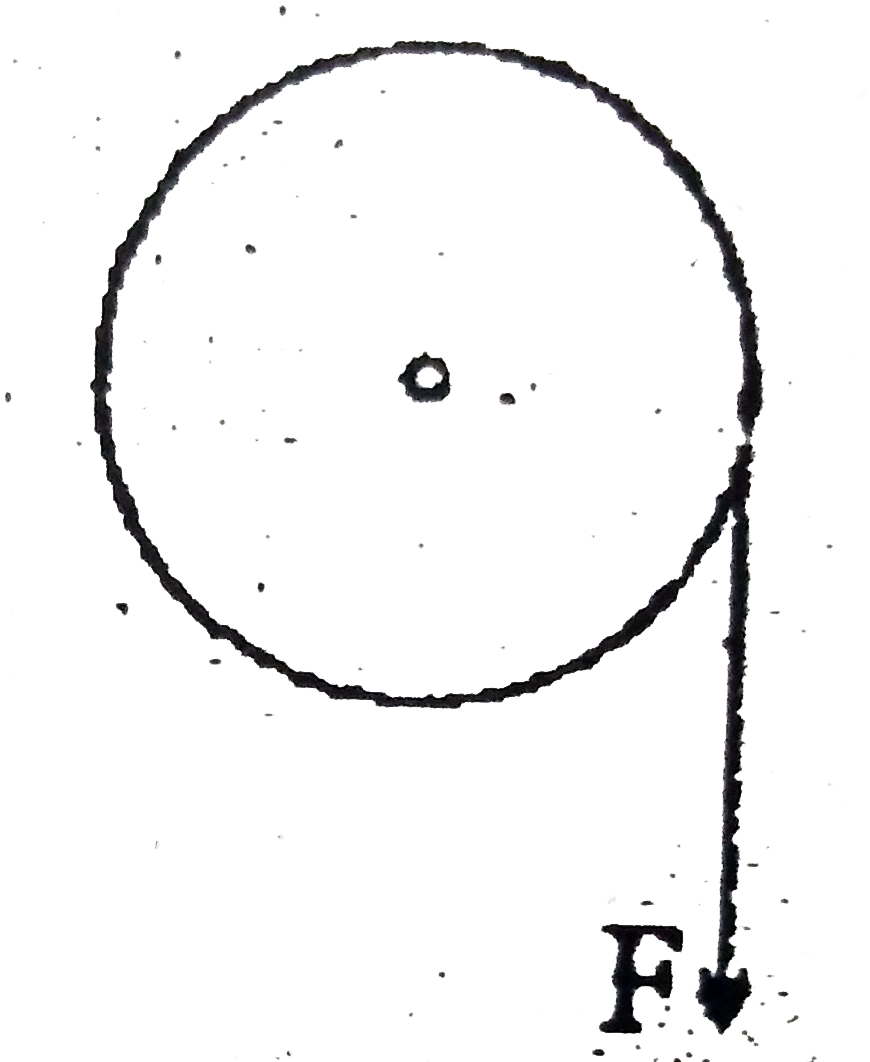 A2gBgCg/2Dg/4
A2gBgCg/2Dg/4A stretched string fixed at both end has n nods, then the lengths of the string is
A(n−1)λ2B(3n+1)λ2C(n+1)λ2D5(n+1)λ2
Vibrations of string fixed at one end
View Solution
A uniform cylider of mass M and radius R has a string wrapped around it. The string is held fixed and the cylinder falls vertically, as in figure.
(a). Show that the acceleration of the cylinder is downward with magnitude a=2g3
(b). Find the tension in the string.
View SolutionFig shown three identical cylinders, cylinders are released, find relation between acceleration of cylinders.

View SolutionA string is wrapped over the edge a uniform disc and the free end is fixed with the ceiling. The disc moves down, unwinding the string. Find the downward acceleration of the disc.
View SolutionA cylinder of mass m suspended by two strings wrapped around the cylinder one near each end, the free ends of the string being attached to hooks on the ceiling, such that the length of the cylinder is horizontal. From the position of rest , the cylinder is allowed to roll down as suspension strings unwind , calculate
(a) The downward linear acceleration of the cylinder
(b) The tension in the strings
(c) The time dependence of the instantaneous power developed by gravity
View Solution
