A uniform round object of mass M, radius R and moment of inertia about its centre of mass Icm has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the celling and the object is released from rest. Find the acceleration of centre of the object and tension n the string. [ Take IcmMR2=k]
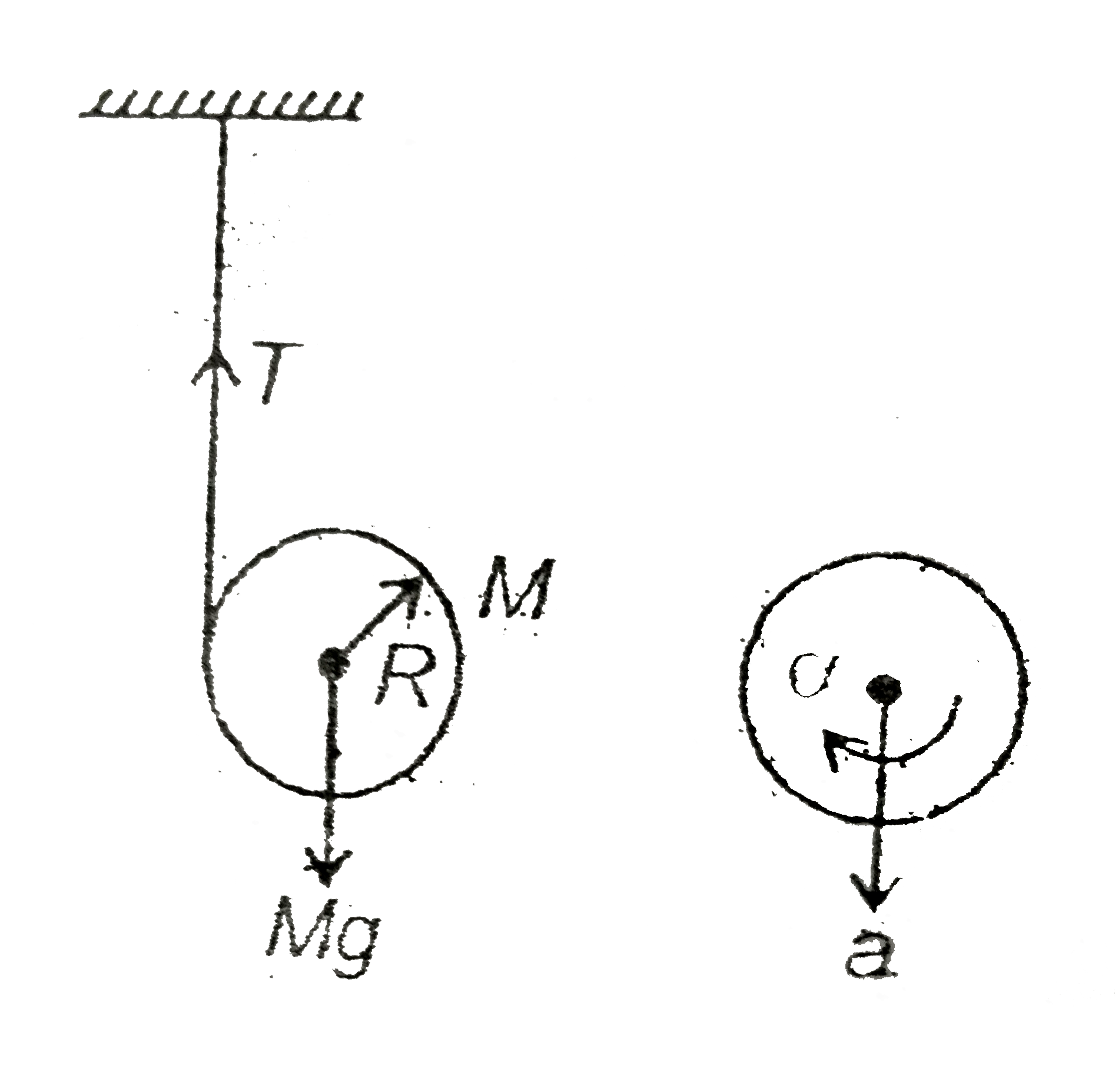
Equation for translatory motion
mg−T=ma…….(1)
Equation for rotatory motion
TR=Icmα……..(2)
Condition for no slipping
a=Rα…….(3)
Solving the equations
Mg−IcmaR2=Ma
a=MgM[1+IcmMR2]=g1+k
T=IcmaR2=(k1+k)Mg
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTEChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Illustration
Explore 4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTEChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Assignment (Section - A) Objective Type Questions (One option is correct)
Explore 62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:AAKASH INSTITUTEChapter:SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:Assignment (Section-D (Assertion and reason))
Explore 5 Videos
- TEST 1Book:AAKASH INSTITUTEChapter:TEST 1Exercise:EXERCISE
Explore 9 Videos
Similar Questions
A disc of mass M has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the ceiling and the disc is released from rest. Find the acceleration of the disc and the tension in the string.
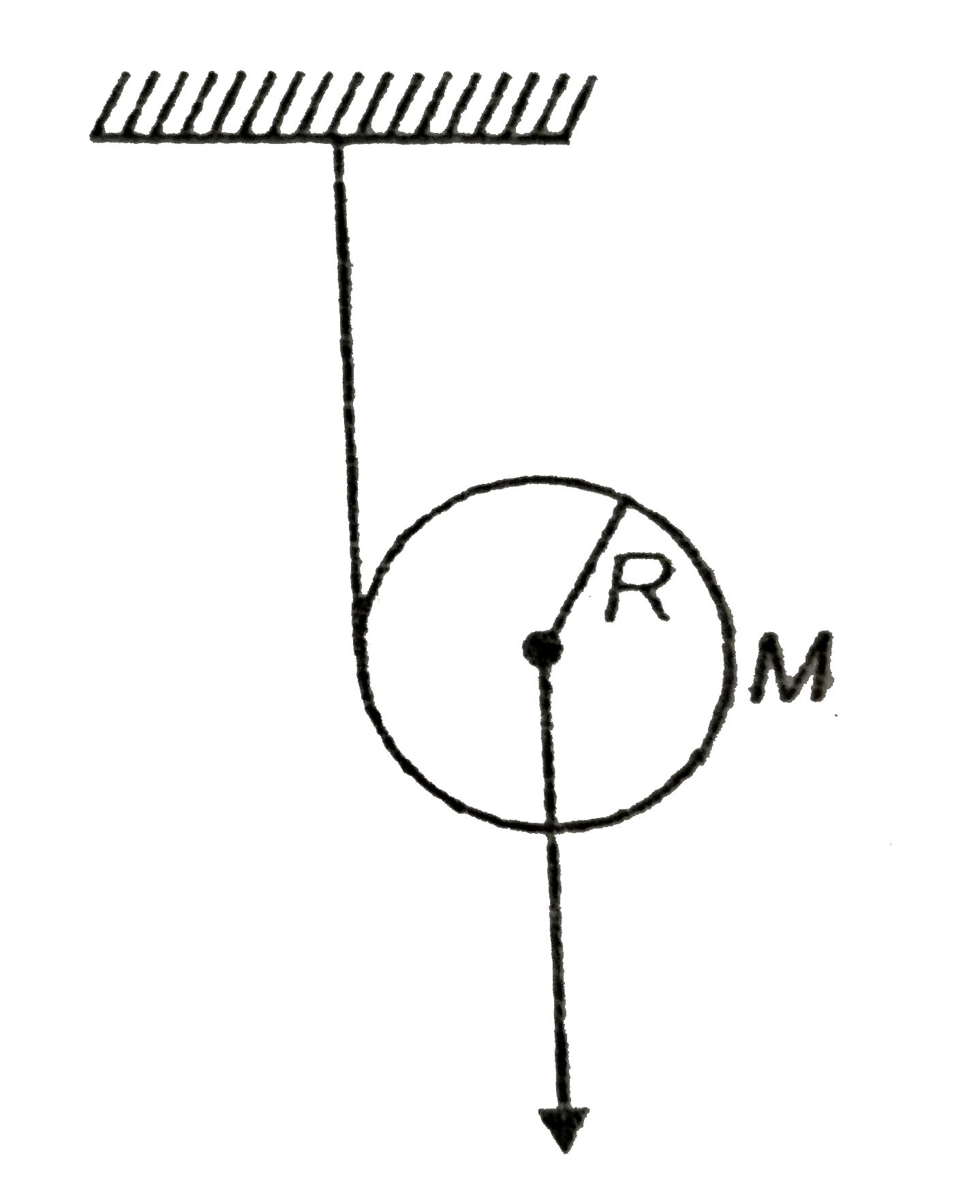
View SolutionA solid cylinder has a thin string wrapped several times around its circumference. The string is fixed at one end and the cylinder is released. Find the downward acceleration of cylinder and tension in the string.
View Solution
Knowledge Check
A block of mass m is attached to one end of a light string which is wrapped on a disc of mass 2m and radius R. The total length of the slack portion of the string is 1. The block is released from rest. The angular velocity of the disc just after the string becomes taut is
 A√glR3B√gl2R2C√2gl3R2D√3gl2R2
A√glR3B√gl2R2C√2gl3R2D√3gl2R2A wheel whose radius is R and moment of inertia about its own axis is I, rotates freely about its own axis. A rope is wrapped on the wheel. A body of mass m is suspended from the free end of the rope. The body is released from rest. The velocity of the body after falling a distance h would be:
A(mghI)1/2B(2mghm+I)1/2C(2mghm+I/r2)1/2D(m+I2mgh)1/2
A uniform disc of radius R and mass M is free to rotate only about its axis. A string is wrapped over its rim and a body of mass m is tied to the free end of the string as shown in the figure. The body is released from rest. Then the acceleration of the body is
View SolutionA wheel of moment of inertia I and rdius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.
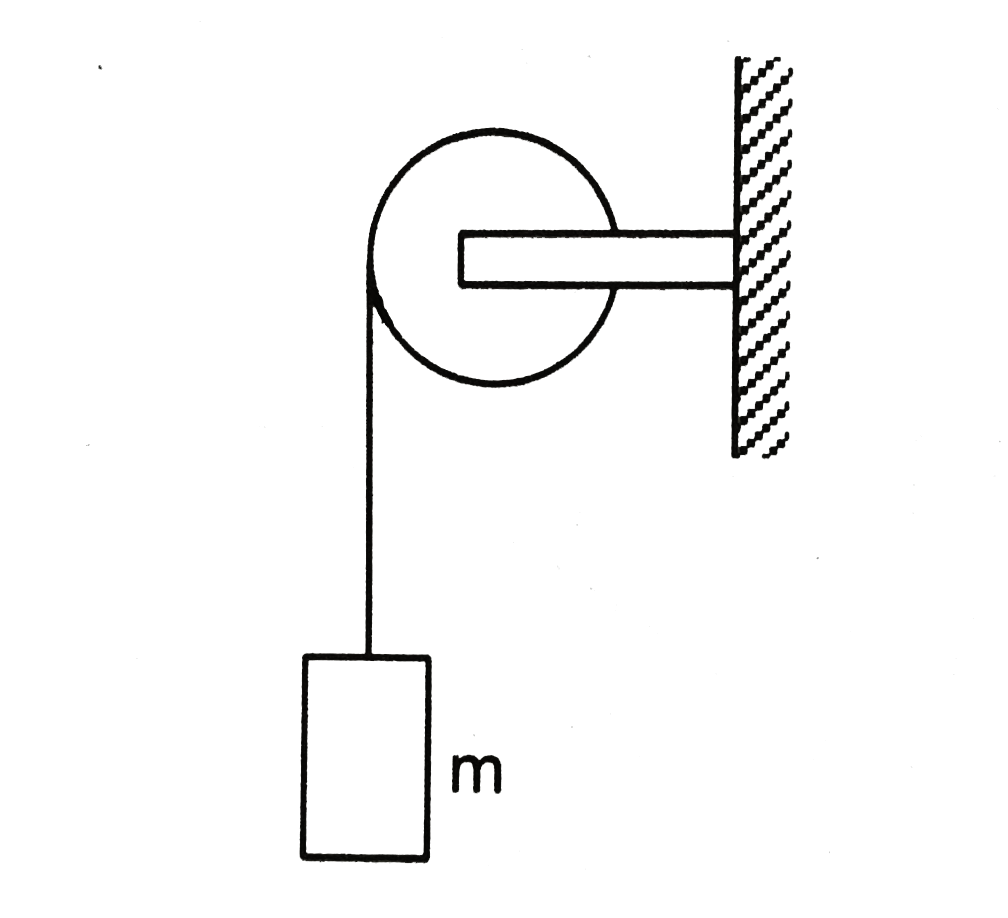
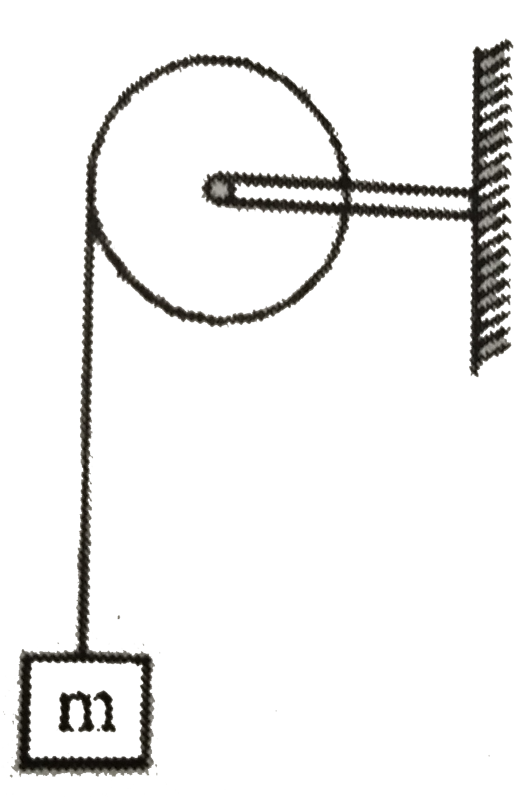
View SolutionA disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-
View SolutionA uniform round body of radius R and mass m and its moment of inertia about centre of mass O is Icm is given. A force F is applied at a height h above the centre of the round body. Find the height h at which force should be applied so that it rolls without friction.
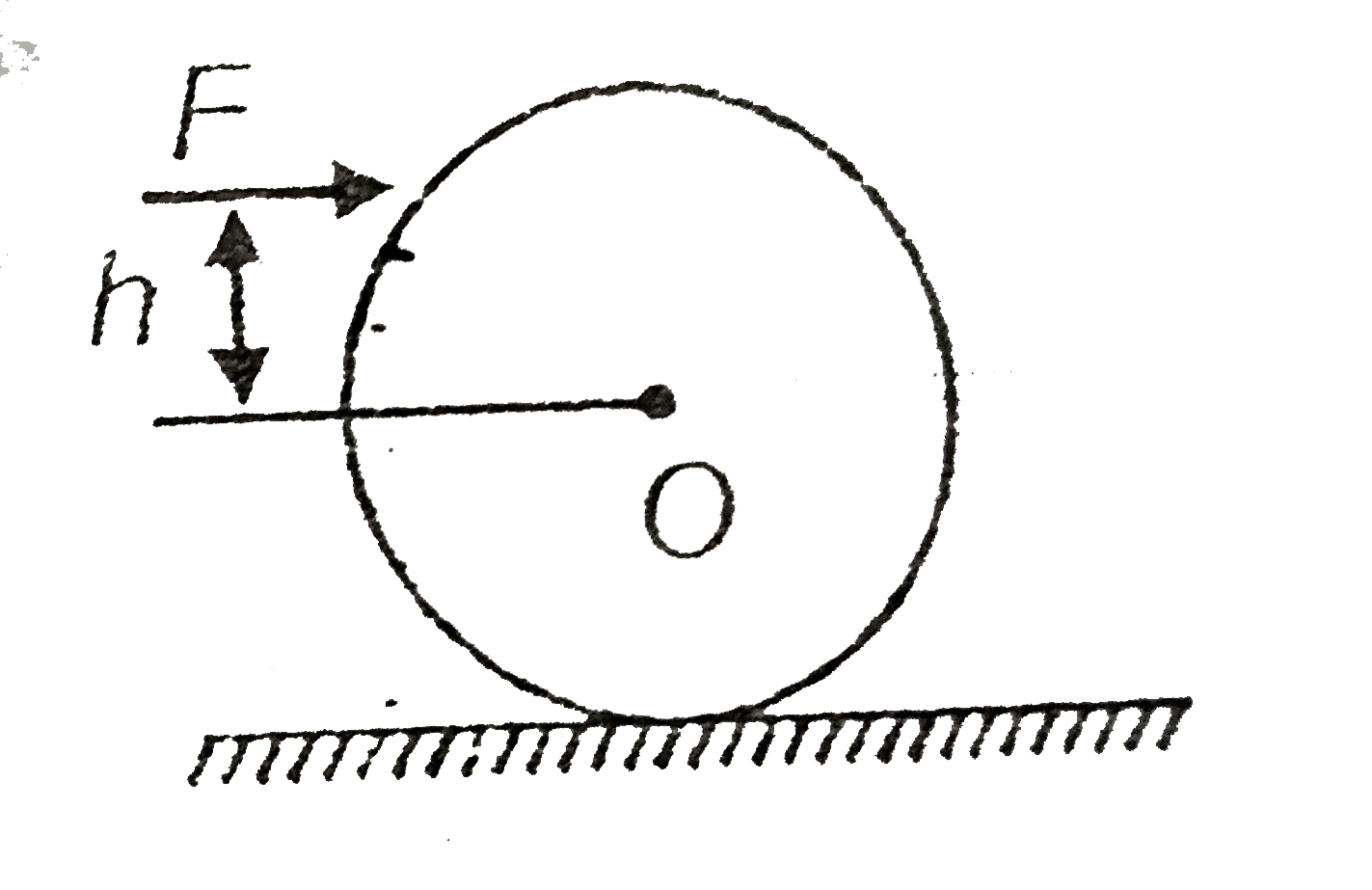
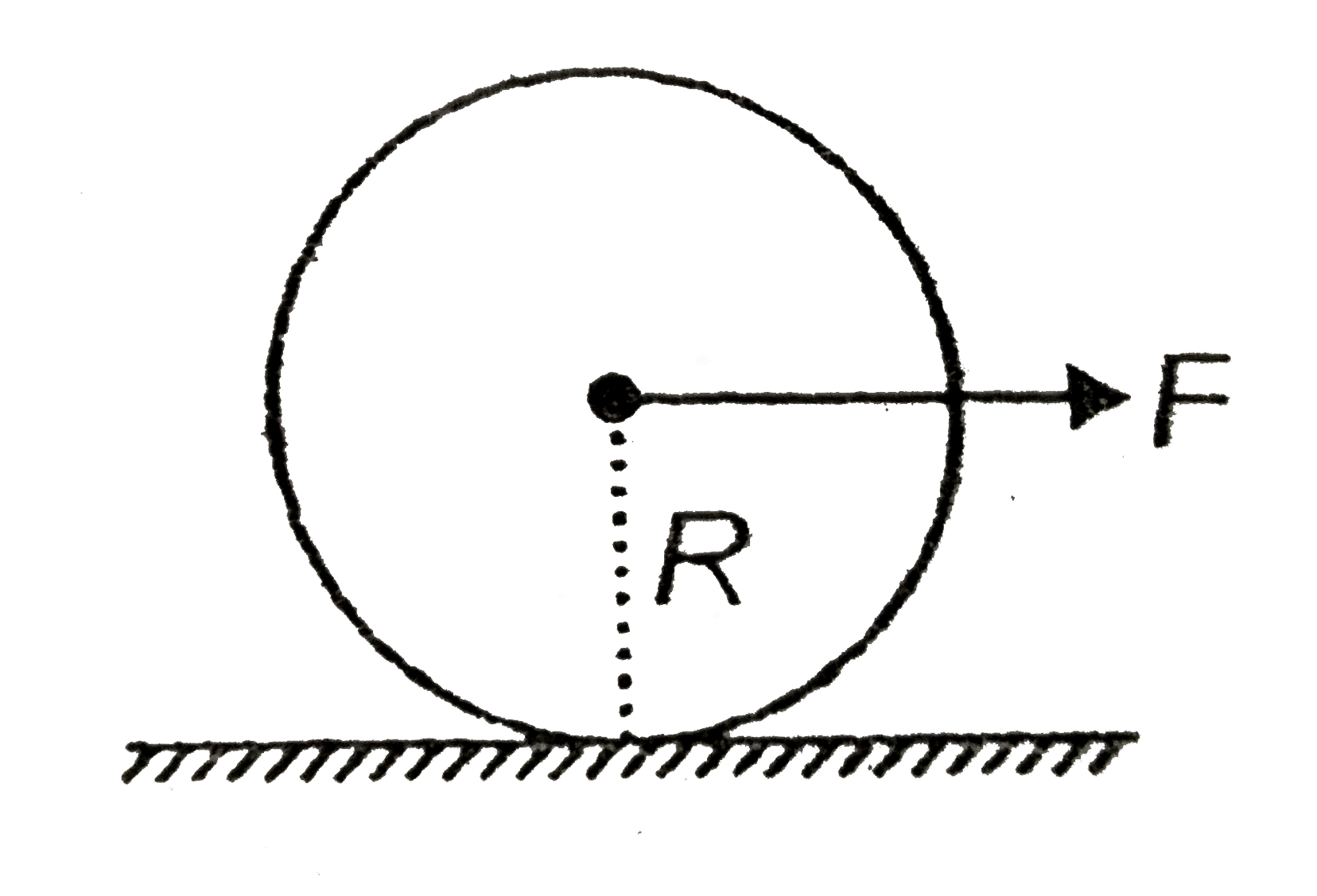
View SolutionA force F is applied at center of a uniform round object of mass m radius R and moment of inertia about its centre of mass Icm. Find (if IcmmR2=k).
(a) Acceleration of center of the round object if it rolls without slipping.
(b) Minimum coefficient of fricition required so that the round object rolls without slipping.
View SolutionA uniform round object of mass m, radius R and moment of inertia about its centre of mas Icm is thrown with speed v. (Without any rotation) on a rough horizontal surface of coefficient of fricition μ. Find (take IcmmR2=k)
(a) Time after which slipping stops
(b) Speed of the round object after slipping stops
(c) Angular speed of the round object after slipping stops
View Solution

