Let us consider a boat which moves with a velcity vbe=5kmh−1 relative to water, At time t=0, the boat passes through a piece of cord floating in water while moving downstream. If itturns back at time t=t1, when and wher does the boat meet the cork again ? Assume t1=30min,
t=0
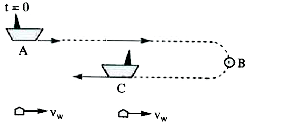
Consider an observer attached with cork. The boat has same speed upstream and downstream realtive to cork. Hence, if the boat travels for 30min. While moving away from cork, t travels the same time while approaching the cork.
Therefore the boat meet the cork at T=2t=60min. = 1h
The distance travelled by boat in this time,
S=VBW×T=5×1=5km
Similar Questions
A boat is moving with a velocity vbw=5km/hr relative to water. At time t=0.the boat passes through a piece of cork floating in water while moving down stream.If it turns back at time t1=30min.
a) when the boat meet the cork again?
b) The distance travelled by the boat during this time.
View SolutionA boat moves with speed of 5 km/h relative to water in a river flowing with a speed of 3 km/h and having a width of 1 km. The minimum time taken around a round trip is
View SolutionA boat can be rowed in still water at a speed u. The boat is moving downstream in a river in which water flows at a speed v. There is raft floating in water and therefore moving along with water at speed v. Let the boat overtakes the raft at the moment t = 0.
Let the boat turns back at time t=t0 and starts moving towards the raft. The separation between the raft and boat after a time interval t' measured from the moment of turning back is
View SolutionWhen a boat travels in a river (strictly in a straight line), it can go either in the direction of flow of river (i.e downstream) or in the direction opposite the flow of river (i.e. upstrem ). Thus the boat's actual speed is more than by which it can move in stationary water while travelling downstram (as river's flow speed is added to it) and less while travelling upstream (as the boat moves against the flow of river).Based on the given information answer the following questions A boat going downstream in a following river overcome a raft at a point P. 1 h later it turned back and after some time passed the raft at a distance 6 km from point P.
After reversing its direction ,how much time was taken by the boat to meet the raft again ( i.e. 2nd time) ?
View SolutionA boat can be rowed in still water at a speed u. The boat is moving downstream in a river in which water flows at a speed v. There is raft floating in water and therefore moving along with water at speed v. Let the boat overtakes the raft at the moment t = 0. Let the boat turns back at time t = t0 and starts moving towards the raft.
After how much time, measured from the moment of turning back the boat will cross the raft again ?
Option 1 t0
Option 2 ut0u+v
Option 3 vt0u+v
Option 4 (v+v)t0u−v
View SolutionA boat can be rowed in still water at a speed u. The boat is moving downstream in a river in which water flows at a speed v. There is raft floating in water and therefore moving along with water at speed v. Let the boat overtakes the raft at the moment t = 0.
The distance between the boat and raft at a later instant of time t is
View SolutionA motor boat of mass m moves along a lake with velocity V0. At the moment t=0 the engine of the boat is shut down. Assuming the resistance of water is proportional to the velocity of the boat →F=−r→v
Q. How long the motor boat with the shut down engine.
View SolutionA boat covers certain distance between two spots on a river taking 't1' time, going down stream and 't2' time goind upstream, what time will be taken by the boat to cover the same distance in still water:-
View SolutionA man swims across a river with speed of 5kmh−1 ( in still water). While a boat goes upstream with speed 12kmh−1 ( in still water). How fast and in which direction does, the man appear to go to the boatman ? Given that the speed of flowing water is 2kmh−1
View SolutionWhen a boat travels in a river (strictly in a straight line), it can go either in the direction of flow of river (i.e downstream) or in the direction opposite the flow of river (i.e. upstrem ). Thus the boat's actual speed is more than by which it can move in stationary water while travelling downstram (as river's flow speed is added to it) and less while travelling upstream (as the boat moves against the flow of river).Based on the given information answer the following questions A boat going downstream in a following river overcome a raft at a point P. 1 h later it turned back and after some time passed the raft at a distance 6 km from point P.
Now, it instead of 6 km they have met at 8 km from point P. Find the speed of river
View Solution