A boat is moving with a velocity vbw=5km/hr relative to water. At time t=0.the boat passes through a piece of cork floating in water while moving down stream.If it turns back at time t1=30min.
a) when the boat meet the cork again?
b) The distance travelled by the boat during this time.
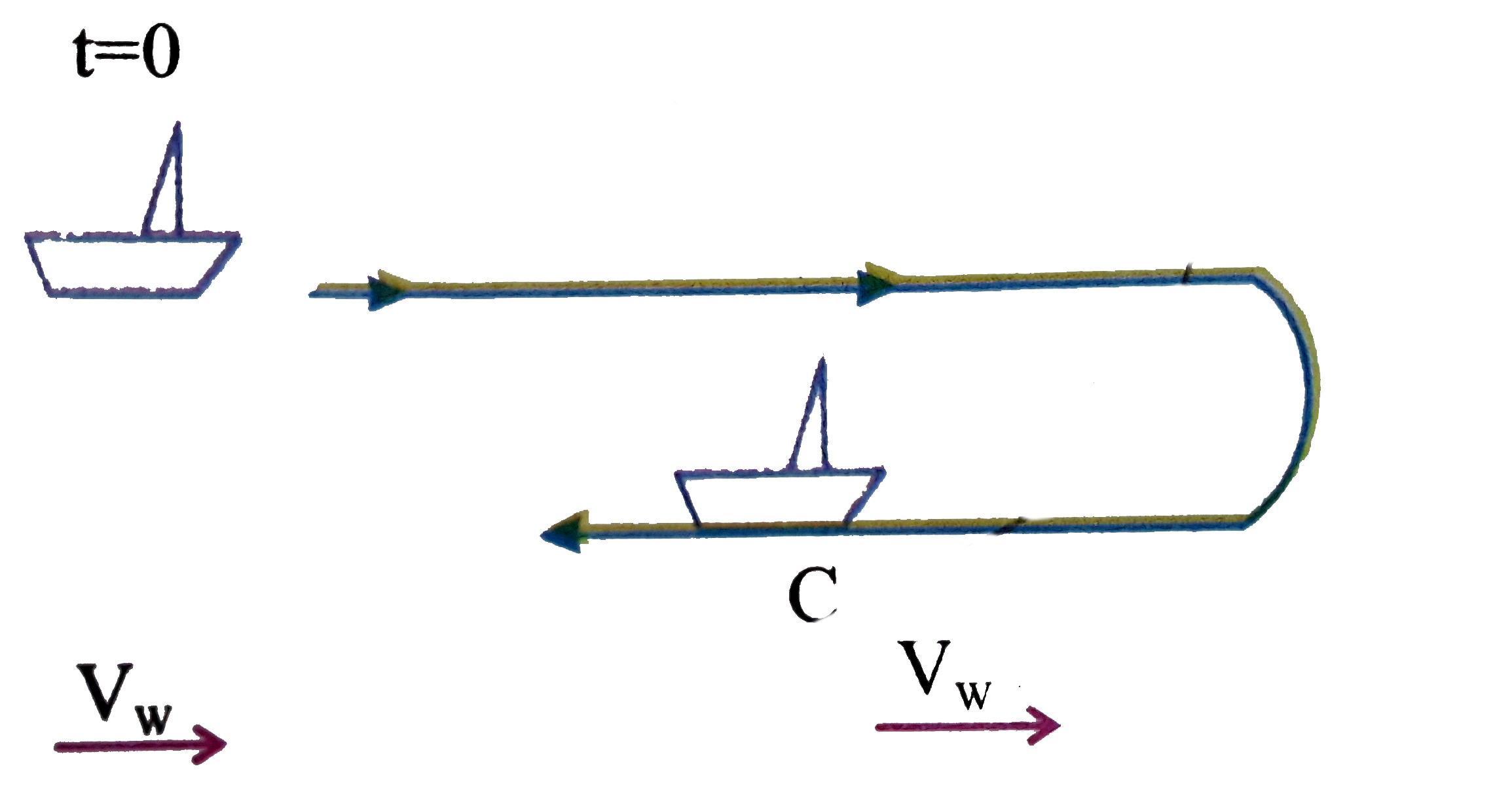
Time of travelling of both from A to B ,(T1) and B to C , (T'1=time of moving the cork from A to C.
 .
.
Velocity of boat from A to B
→vb,w+vedcvw=(5+u)kmh−1
And velocity of boat from B to C
→vb,w+vedcvw=(5+u)kmh−1
Distance moved by boat in time t'1
AB=(5+4)t1
And disannce moved by boat in timet'1=BC=(5−u)t'1
Distance moved by cord during this time
AC=u(t1+t'1)
But AB=AC+BC
(5+u)t1=u(t1+t'1)+(5−u)t'1
5t1=5t'1⇒t'1=t1=30min
Hence, the cord meets the boat again aftre 1h.
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Solved Examples
9 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.1
17 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
A boat takes 4 hrs to travel certain distance in a river in down stream and it takes 6 hrs to travel the same distance in upstream. Then the time taken by the boat to travel the same distance in still water is
View SolutionA boat can be rowed in still water at a speed u. The boat is moving downstream in a river in which water flows at a speed v. There is raft floating in water and therefore moving along with water at speed v. Let the boat overtakes the raft at the moment t = 0.
The distance between the boat and raft at a later instant of time t is
View SolutionA boat moves with speed of 5 km/h relative to water in a river flowing with a speed of 3 km/h and having a width of 1 km. The minimum time taken around a round trip is
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :
View SolutionA swimmer capable of swimming with velocity v relative to water jumps in a flowing river having velocity u. The man swims a distance d down stream and returns back to the original position. Find out the time taken in complete motion.
View SolutionA boat can be rowed in still water at a speed u. The boat is moving downstream in a river in which water flows at a speed v. There is raft floating in water and therefore moving along with water at speed v. Let the boat overtakes the raft at the moment t = 0.
Let the boat turns back at time t=t0 and starts moving towards the raft. The separation between the raft and boat after a time interval t' measured from the moment of turning back is
View SolutionA boat can be rowed in still water at a speed u. The boat is moving downstream in a river in which water flows at a speed v. There is raft floating in water and therefore moving along with water at speed v. Let the boat overtakes the raft at the moment t = 0. Let the boat turns back at time t = t0 and starts moving towards the raft.
After how much time, measured from the moment of turning back the boat will cross the raft again ?
Option 1 t0
Option 2 ut0u+v
Option 3 vt0u+v
Option 4 (v+v)t0u−v
View SolutionA boat covers certain distance between two spots on a river taking 't1' time, going down stream and 't2' time goind upstream, what time will be taken by the boat to cover the same distance in still water:-
View SolutionA boat of mass 90 kg is floating in still water. A boy of mass 30 kg walks from one end to the other on it. If the length of the boat is 3 m, then the distance through which the boat will move is
View SolutionTwo boats A and B are moving along perpendicular paths in a still lake at night. Boat A move with a speed of 3m/s and boat B moves with a speed of 4m/s in the direction such that they collide after sometime. At t=0, the boats are 300m apart. The ratio of distance of distance travelled by boat A to the distance travelled by boat B at the instant of collision is :-
View Solution
