A particle moving with uniform acceleration along a straight line ABC rosses point A at t=0 with a velocity 12ms−1.B is 40m away from A andC is 64m away from A. The particle passes B at t=4 s.a.Afterwˆtimewillthepartic≤beatC?b.WˆisitsvelocityatC?c.Wˆdoesthepartic≤reachAaga∈?d.Locatethep∮wherethepartic≤reversesitsdirectionofmotion.e.F∈dthedistancecoveredbythepartic≤∈thefirst15 s.
Let the acceleratuib of the oartucke be (a)
 .
.
For motion between A and B
u=12ms−1,s=40 m, t=4 s<br>s=ut+1//2 at^(2)<br>rArr 40=12xx4+(1)/(2)xxaxx(4)^(4) rArra=-1 m s^(-2)<br>Formotionberween A and C<br>64=12t+(1)/(2)(-1)t^(2)<br>rArrt^(2)-24 t+128=0<br>rArr (t-8)(t-16)=0<br> rArr t=8 s, 16 s<br>a.Thepartic≤willbeatCtwo,att=8 sand1=16 s.<br>b.Velocityofthepartic≤atc<br>Att=8 s,velocityofthepartic≤v=12+(-1)xx8<br>=4 m s^(-1)<br>Att=16 s,velpcotyofthepartic≤v=12+(-1) xx16<br>=-4 m s^(-1)<br>Astheae≤rationofthepartic≤is¬ative,itwillrηrdasitmovesalonABC.Atap∮beyondCi.e.,atD,thepartic≤willcome→restmomentarily,andthenitwillmovebackwardwith∈creasingspeed.Throughoutthemotion,thepartic≤dece≤rates,itsvelocitydecrasescont∈uously,velocityvariesas(12,11,10,...,2,1,0,−1,−2,...,−10,−11,−12,)etc.OnlyomA→Dthemotionisrηrded,dur∈gwhichspeedvariesas(12,11,10,...,2,1,0.)<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V01_C04_S01_058_S02.pngwh=80%mx-autosty≤=background:white;>.<br>Subsequently,thepartic≤speedsup,speedchang∈gas(1,2,3,....,)etc.<br>Noticethed⇔erncebetweendece≤rationandrηrda−tion.<br>c.Whenthepartic≤reachesAaga∈,itsdisplacement=0
becuase0=12×t+12(−1)t2
⇒t=0,24s
At t=0, Velocity at A=12ms−1,
At t=24s, velocity at A is
12+(−1)×24=−12ms−1.
d. The particle reveses the direction of motion at D. For the motion between A and D
 .
.
u=12ms−1,v=0,a=−1ms−2. If AD=s, From the equation
v2=u2+2as
(0)2^(2)+2×(−1)×s
s=12×22=72m
You can also calculate the time taken by the particle to reach D from 0=12+(−1)tD and then
from s=12×tD+12(−1)t2D, you can find s.
But then again you must be intersted in optimising the steps of calculation and must not proceed so
c. After 12s the particle comes to rest momentarily at D after covering a distance of 72m.
 .
.
Distance in subsequent 3s
=0×3+12×(−1)×(3)2=4.5m
becuased=72m+4.5m=76.5m.
Topper's Solved these Questions
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.1
17 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.2
12 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
Similar Questions
A particle, moving with uniform acceleration along a straight line ABC, crosses point A at t = 0 with a velocity 12 m/s. B is 40 m from A and C is 64 m from A. The particle passes B at t = 4 s.
(a) At what time, will the particle be C?
(b) What is its velocity at C?
View SolutionA particle moving with uniform acceleration from A to B along a straight line has velcities v1 and v2 at A and B respectively. If C is the mid-point between A and B then determine the velocity of the particle at C .
 .
.
View SolutionThe velocity-time graph of a particle in straight line motion is velocity-time graph of a particle in straight line motion is shown in. The particle starts its motion from origin.
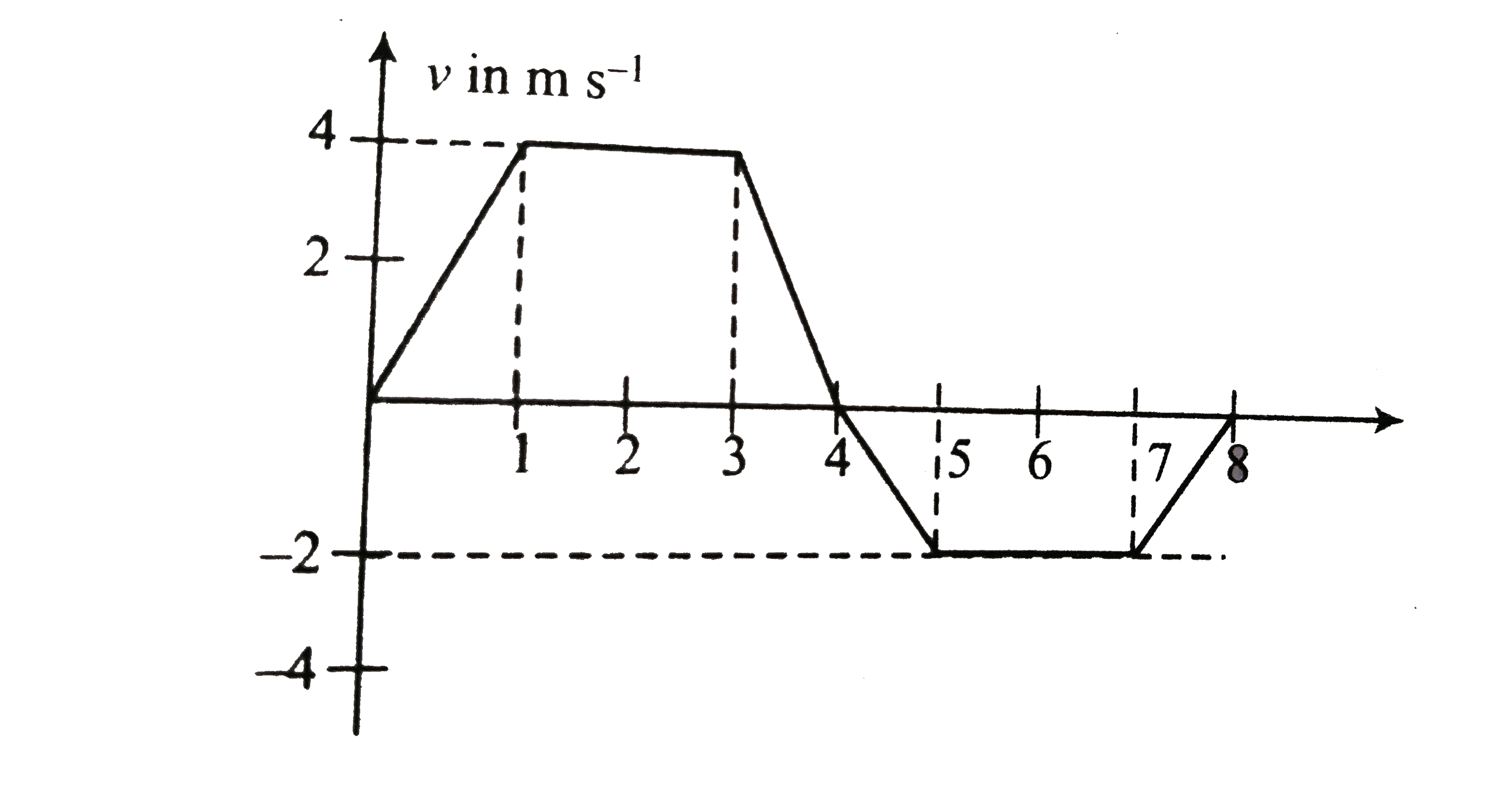 .
.
The distance of the particle from the origin after 8s is .
View SolutionA particle is moving with uniform acceleration along a straight line. Its velocities at A & B are respectively 7m/s & 17m/s. M is mid point of AB. If t1 is the time taken to go from A to M and t2 the time taken to go from M to B, the ratio t1t2 is equal to :-
View SolutionA particle goes from A to B in 10s with uniform acceleration. Its velocity at A and B are 5 m/s and 25 m/s. Its acceleration (in m/s2) is
View SolutionA particle moving along a straight line with uniform acceleration has velocities 7m/s at A and 17m/s at C. B is the mid point of AC. Then :-
View SolutionA particle moves with a uniform velocity of 50 m/s for 20 min. What is the velocity of particle at t = 2 min ?
View SolutionA particle starts to move in a straight line from a point with velocity 10 m s−1 and acceleration - 2.0 ms−2. Find the position and velocity of the particle at (i) t = 5 s, (ii) t' = 10 s.
View SolutionThe acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.

View SolutionA particle moving with uniform acceleration passes the point x=2m with velocity 20m/s at the instant t=0. Some time later it is observed at the point x=32m moving with velocity 10m/s.
(a) What is its acceleration?
(b) Find its position nd velocity at the instant t=8s.
(c) What is the distance traveled during the interval t=0 to 8s?
View Solution
