An aeroplane flies along a straight path AandB and returns back again. The distance between AandB is l and the aeroplane maintains the constant speed v w.r.t. wind.
There is a steady wind with a speed u at an angle θ with line AB. Determine the expression for the total time of the trip.
 .
.
A to B
Velocity of plane alongAB=vcosα−ucosθ,
and for no - drift from line .
AB: vsinα=usinθ⇒sinαusinθv
time taken from A to B tAB=lvcosα−ucosθ

B to A
velocity of plane along BA=vcosα+ucosθ
and for no drift from line AB: vsinα=usinθ⇒sinαusinθv
total time taken tAB+tBA=2vlcosαv2cos2α−u2cos2θ=2vl√1−u2sin2θv2v2−u2
Similar Questions
An aeroplane is to go along straight line from A to B, and back again. The relative speed with respect to wind is V. The wind blows perpendicular to line AB with speed v. The distance between A and B is l. The total time for the round trip is:
View SolutionAn eaeroplane is to go along straight line from A to B, and back again. The relative speed with respect to wind is V. The wind blows perpendicular to line AB with speed v. The distance between A and B is l. The total time for the round trip is:
View SolutionAn airplane flies northward from town A and B and then back again. There is a steady wind blowing towards the north so that for the first state of the trip, the airplane is flying in the same direction as the wind and for the return trip of the journey, the airplane is flying opposite of the wind. The total trip time Tω as compared to the total trip time in the absence of any winds T0 is:
View SolutionTwo paricles A and B of equal masses m are t ied with an inextensible string of length 2l. The initial distance between A and B is l. Particle A is given speed v as shown. Find the speed of particie A and B just after the string becomes taut.
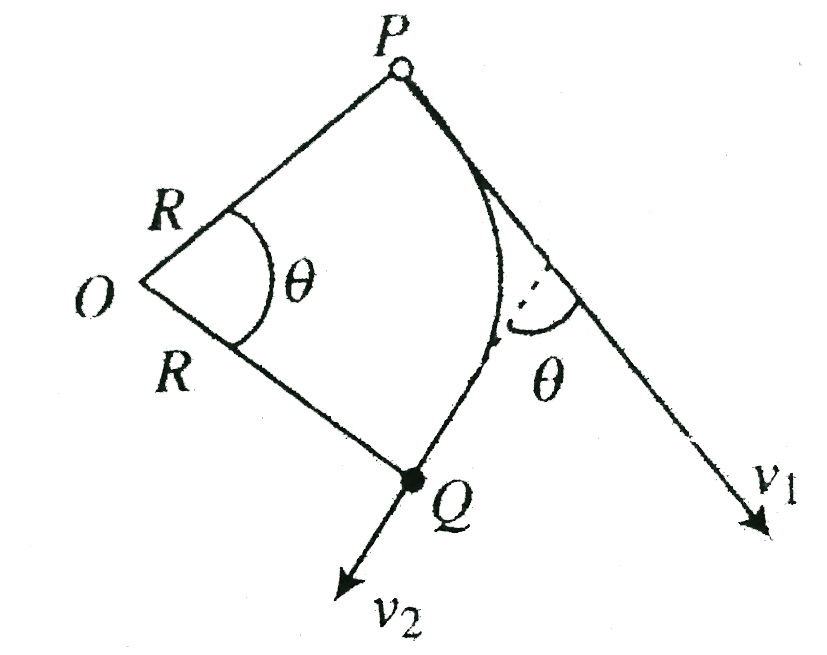
View SolutionA particle describes an angle θ in a circular path with a constant speed v. Find the a charge in the velocity of the particle and b average acceleration of the particle during the motion in the curve (circle).
 .
.
View SolutionA scooter is moving along a straight line AB covers a distance of 360 m in 24 s and returns back from B to C and coveres 240 m in 18 s. Find the total distance travelled by the scooter.
View SolutionA man wants to swim in a river from A→B and back from B→A always following line AB (Fig. 5.94). The distance between points AandB is S. The velocity of the river current v is constant over the entire width of the river. The line AB makes an angle ∝ with the direction of current. The man moves with velocity u at angle β to the line AB. The man swim to cover distance AB and back, find the time taken to complete the journey.
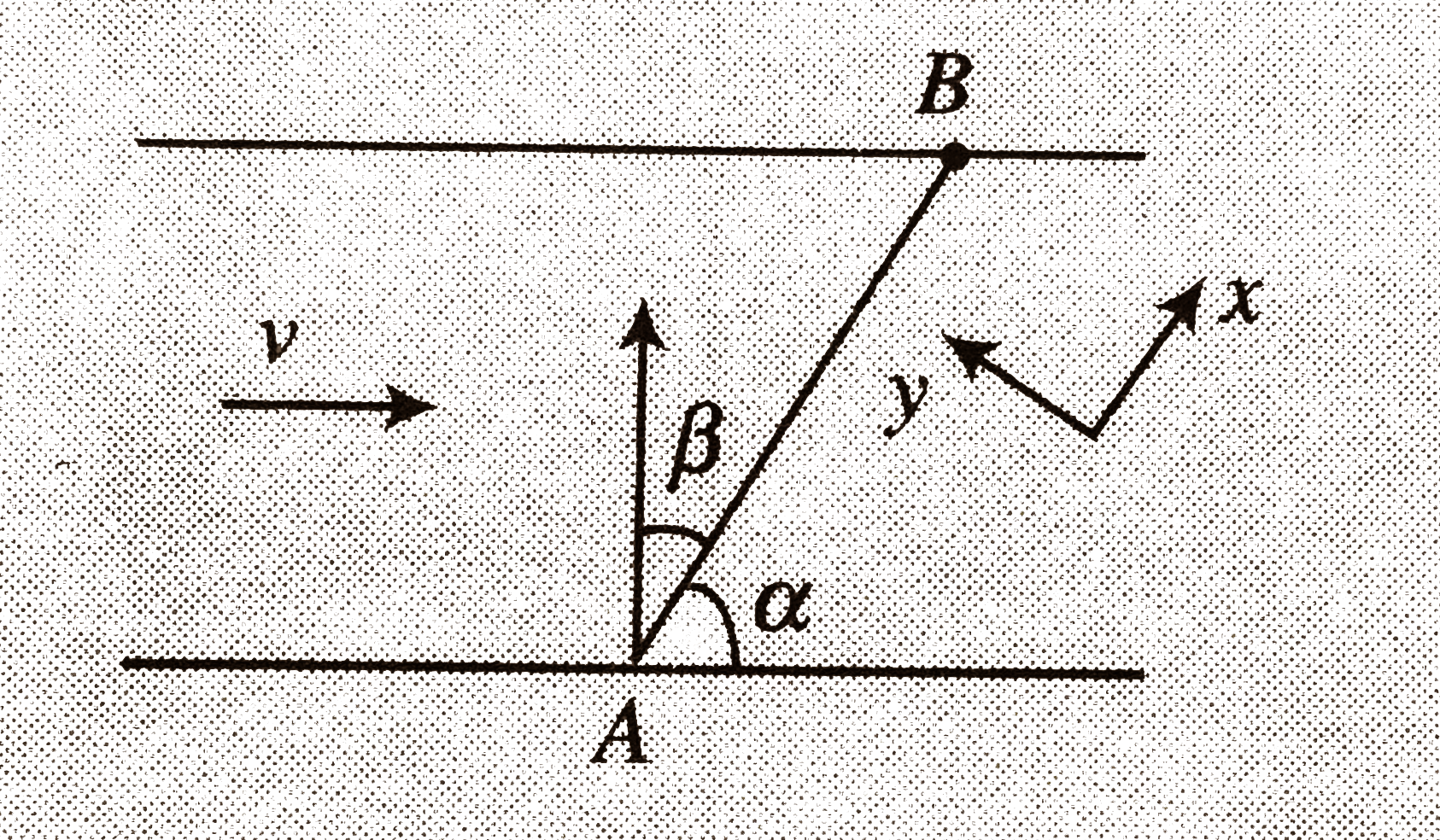 .
.
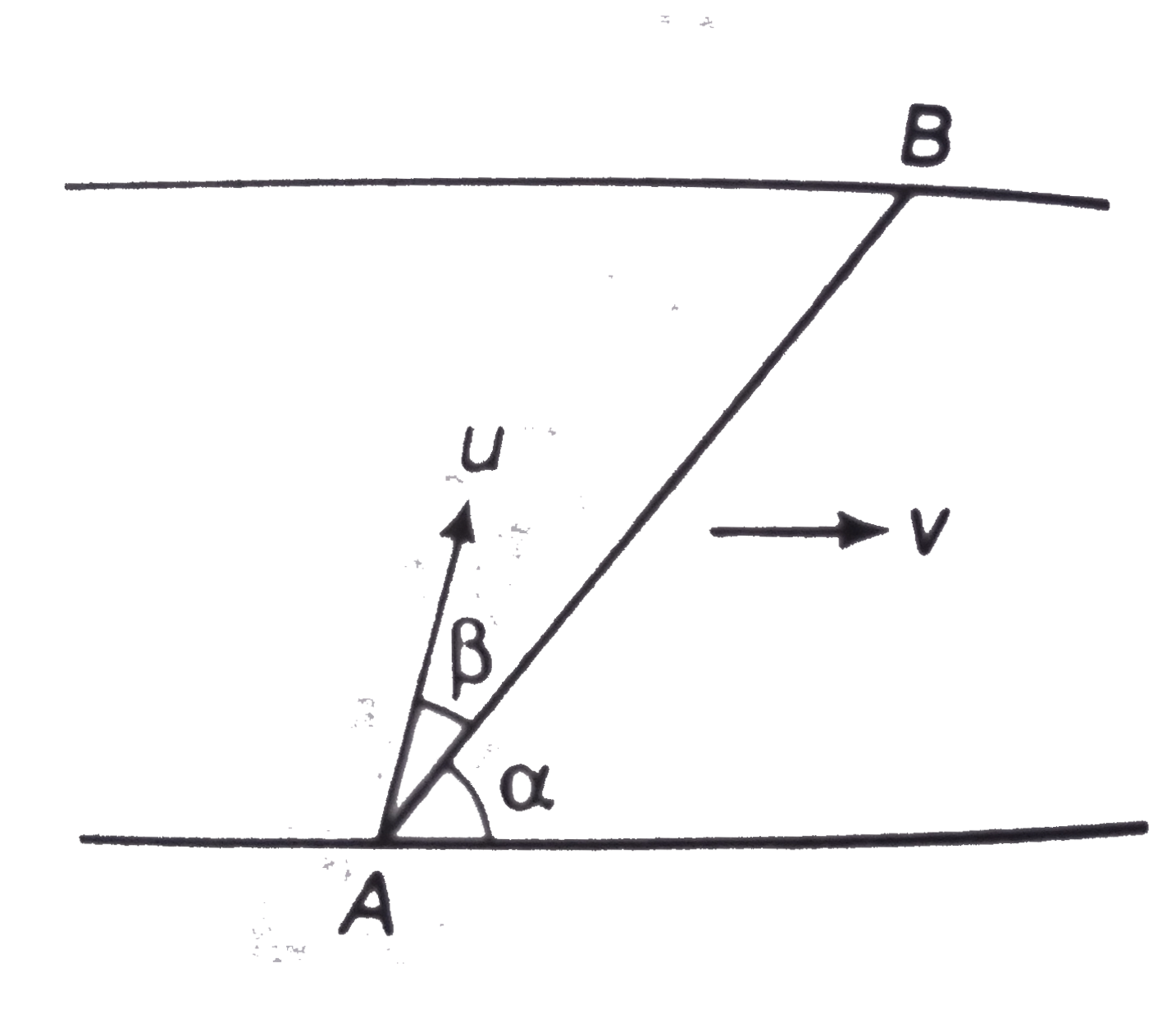
View SolutionA launch plies between two points A and B on the opposite banks of a river always following the line AB. The distance S between points and B is 1200 m. The velocity of the river current v=1.9m/s is constant over the entire width of the river. The line AB makes an angle α=60∘ with the direction of the current. With what velocity u and at what angle beta to the line AB should the launch move to cover the distance AB and back in a time t=5min? The angle beta remains the same during the passage from A to B and from B to A.
View SolutionA metallic rod of length l is rotated at a constant angular speed ω, normal to a uniform magnetic field B. Derive an expression for the current induced in the rod, if the resistance of the rod is R.
View SolutionA U-shaped wire has a semicircular bending between A and B as shown in Fig. A bead of mass m moving with uniform speed v through a wire enters the semicircular bend at A and leaves at B with velocity v/2 after time T. The average force exerted by the bead on the part AB of the wire is
View Solution
