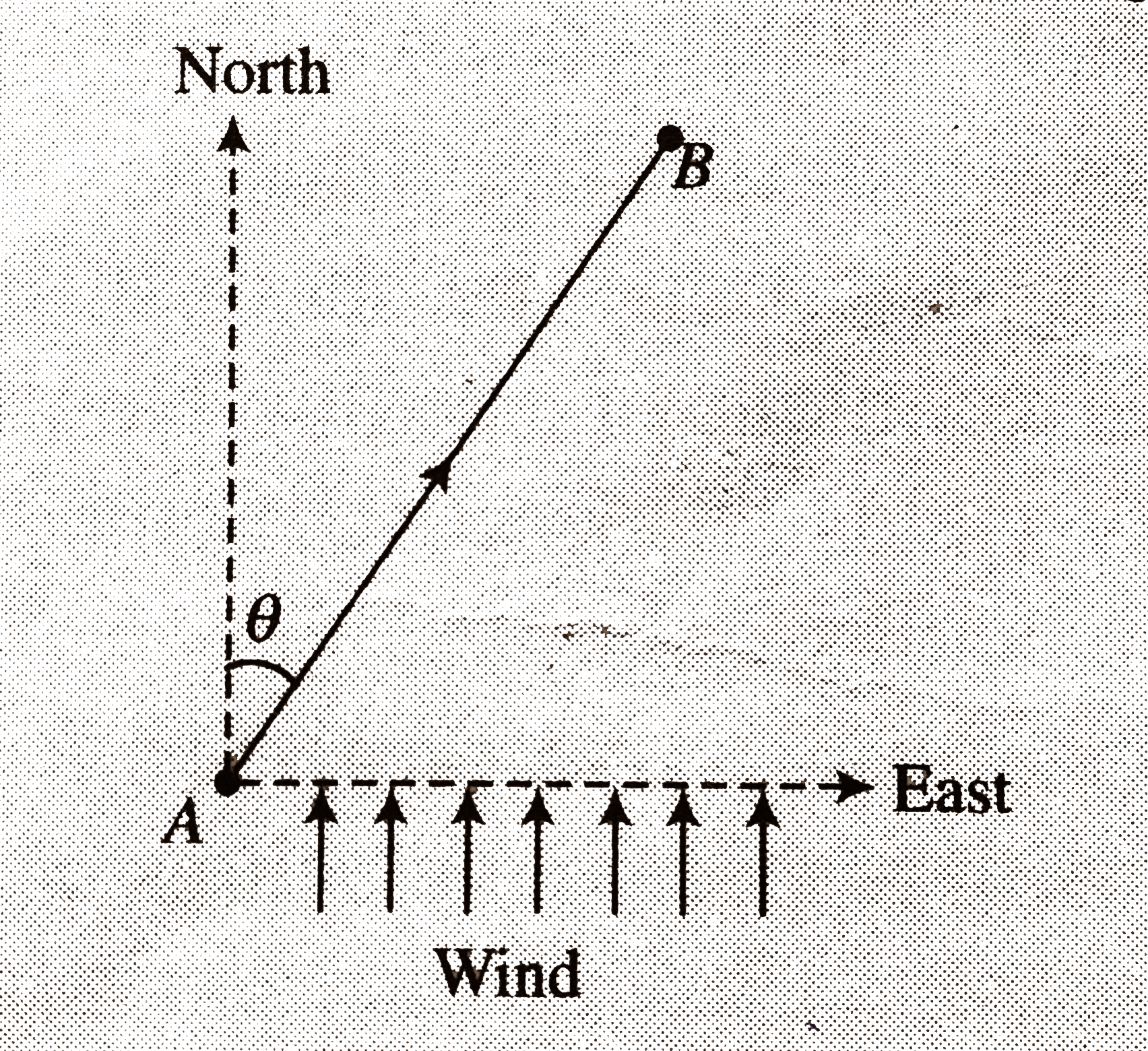
An eaeroplane is to go along straight line from A to B, and back again. The relative speed with respect to wind is V. The wind blows perpendicular to line AB with speed v. The distance between A and B is l. The total time for the round trip is:
2l√V2−v2
2vlV2−v2
2VlV2−v2
2l√V2+v2
The correct Answer is:A

For no drift:Vsinθ=v
sinθ=vV ∵ t=tAB+tBA
t=2lVcosθ=2lV√1−υ2V2⇒t=2l√V2−υ2
Similar Questions
An aeroplane flies along a straight path AandB and returns back again. The distance between AandB is l and the aeroplane maintains the constant speed v w.r.t. wind.
There is a steady wind with a speed u at an angle θ with line AB. Determine the expression for the total time of the trip.
 .
.
View SolutionA particle moves in a straight line from A to B with speed v1 and then from B to A with speed v2. Find the average velocity and average speed.
View Solution
Knowledge Check
An aeroplane flies along straight line from A to B and backs again to the same point. There is a steady wind speed v. The distance between A and B is l still air speed of the aeroplane is V, then:
ATotal time for the round trip, if the wind blows along the line AB, is2Vlv2−v2BTotal time for the round trip, if the wind blows perpendicular to the line AB, is 2l√V2−v2CTotal time for the round trip depends on the direction of wind.DTotal time for the round trip is independent of direction of wind.An aeroplane flies along a straight line from A to B with a speed v0. A steady wind v is blowing if AB=l then
a)total time for the trip is 2v0lv20−v2 if wind blows along the line AB
b)total time for the trip is 2l√v20−v2,if wind blows perpendicular to the line AB
c)total time for the trip decrease because of the pressure of wind
d)total time for the trip increase because of the presence of windAa,b,d are correctBa,b,c are correctConly a,d are correctDonly b,d are correctA body starting from rest moves along a straight line with a constant acceleration. The variation of speed (v) with distance (s) is represented by the graph
A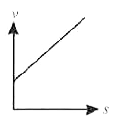 B
B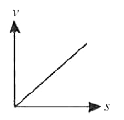 C
C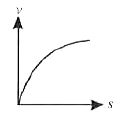 D
D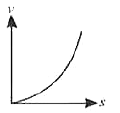
A particle moves in a straight line from A to B
(a) for the first half of distance with speed v1 and the next half of distance with speed v2.
(b) for the first one-third distance with speed v1 and the next two-third distance with speed v2.
(c ) for the first one-fourth distance with speed v0, the next half of distance with speed 2v0 and the last one-fourth distance with speed 3v0.
Find the average speed in each case.
View SolutionA helicopter files horizontally with constant velocity in a direction θ east of north between two points AandB, at distance d apart. Wind is blowing from south with constant speed u, the speed of helicopter relative to air is nu where n>1. find the speed of the helicopter along AB. The helicopter returns from B to A with same speed nu relative to air in same wind. Find the total time for the journeys.
 .
.
View SolutionA particle travels along a straight line. It covers halg the distance with a speed (v). The remaining part of the distance was covere with speed v1 for half the time and with speed v2 for the other half the time . Find the average speed of the particle over the entire motion.
View SolutionA body starting from rest moves along a straight line with a constant acceleration. The variation of speed (v) with distance (s) is represented by the graph
View SolutionAn airplane flies northward from town A and B and then back again. There is a steady wind blowing towards the north so that for the first state of the trip, the airplane is flying in the same direction as the wind and for the return trip of the journey, the airplane is flying opposite of the wind. The total trip time Tω as compared to the total trip time in the absence of any winds T0 is:
View Solution

