An airplane flies from a town A to a town B when there is no wind and takes a total time T0 for a return trip. When there is a wind blowing in a direction from town A to town B, the plane's time for a similar return trip, Tw, would satisfy
T0<Tw
T0>Tw
T0=Tw
the result depends on the wind velocity between the towns
The correct Answer is:A
To solve the problem, we need to analyze the airplane's travel time under two different conditions: without wind and with wind. Let's break it down step by step.
Step 1: Define the Variables
- Let the distance from town A to town B be x.
- Let the speed of the airplane be v.
- Let the speed of the wind be vw.
- The total time taken for the return trip without wind is T0.
Step 2: Calculate the Time Without Wind
When there is no wind, the airplane travels from A to B and back to A. The total distance for the round trip is 2x. The time taken for the return trip without wind can be expressed as:
T0=2xv
This is our Equation 1.
Step 3: Calculate the Time With Wind
When there is wind blowing from A to B, the airplane's effective speed while flying from A to B becomes v+vw (the speed of the airplane plus the speed of the wind). Conversely, while returning from B to A, the effective speed becomes v−vw (the speed of the airplane minus the speed of the wind).
Time to Fly from A to B:
TAB=xv+vw
Time to Fly from B to A:
TBA=xv−vw
Step 4: Total Time With Wind
The total time for the round trip with wind Tw is the sum of the time taken to fly from A to B and from B to A:
Tw=TAB+TBA=xv+vw+xv−vw
Step 5: Simplify the Expression for Tw
To combine the two fractions, we find a common denominator:
Tw=x((v−vw)+(v+vw)(v+vw)(v−vw))=x(2vv2−v2w)
Thus, we can write:
Tw=2xv2−v2w⋅v
Step 6: Relate Tw to T0
From Equation 1, we know that:
T0=2xv
Now, substituting T0 into the expression for Tw:
Tw=T0⋅11−v2wv2
Conclusion
From our analysis, we can conclude that:
Tw=T0⋅11−v2wv2
This indicates that the time taken with wind Tw is greater than the time taken without wind T0 since v2wv2 is a positive fraction less than 1.
Final Relation
Thus, the final relation we derive is:
Tw>T0
- Let the distance from town A to town B be x.
- Let the speed of the airplane be v.
- Let the speed of the wind be vw.
- The total time taken for the return trip without wind is T0.
When there is no wind, the airplane travels from A to B and back to A. The total distance for the round trip is 2x. The time taken for the return trip without wind can be expressed as:
T0=2xv
This is our Equation 1.
When there is wind blowing from A to B, the airplane's effective speed while flying from A to B becomes v+vw (the speed of the airplane plus the speed of the wind). Conversely, while returning from B to A, the effective speed becomes v−vw (the speed of the airplane minus the speed of the wind).
TAB=xv+vw
TBA=xv−vw
The total time for the round trip with wind Tw is the sum of the time taken to fly from A to B and from B to A:
Tw=TAB+TBA=xv+vw+xv−vw
To combine the two fractions, we find a common denominator:
Tw=x((v−vw)+(v+vw)(v+vw)(v−vw))=x(2vv2−v2w)
Tw=2xv2−v2w⋅v
From Equation 1, we know that:
T0=2xv
Tw=T0⋅11−v2wv2
From our analysis, we can conclude that:
Tw=T0⋅11−v2wv2
This indicates that the time taken with wind Tw is greater than the time taken without wind T0 since v2wv2 is a positive fraction less than 1.
Thus, the final relation we derive is:
Tw>T0
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Exercise-2
30 Videos
- MOTION IN A STRAIGHT LINEBOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Exercise-2
30 Videos
- MOTION IN A PLANE BOOK - DISHA PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Exercise -2 : CONCEPT APPLICATOR
28 Videos
- MOVING CHARGES AND MAGNETISM BOOK - DISHA PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - EXERCISE - 2 : Concept Applicator
25 Videos
Similar Questions
To go from town A to town B a plane must fly about 1780km at an angle of 30∘ west of north.How far north of A is B? is
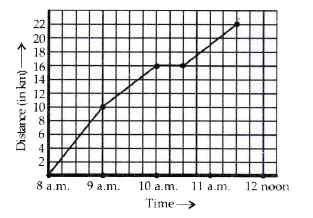
View SolutionA courier-person cycles from a town to a neighboring suburban area to deliver a parcel to a merchant. His distance from the town at different times is shown by the following graph.
(a) What is the scale taken for the time axis?
(b) How much time did the person take for the travel?
(c) How far is the place of the merchant from the town?
(d) Did the person stop on his way? Explain.
(e) During which period did he ride fastest?

View Solution
Knowledge Check
An airplane flies northward from town A and B and then back again. There is a steady wind blowing towards the north so that for the first state of the trip, the airplane is flying in the same direction as the wind and for the return trip of the journey, the airplane is flying opposite of the wind. The total trip time Tω as compared to the total trip time in the absence of any winds T0 is:
ATw=T0BTw>T0CTw<T0DData is insufficientTown D is towards East of town F. Town B is towards North of town D. Town H is towards South of town B . Towards which direction is town H from town F ?
AEastBSouth-eastCNorth-EastDData inadequateTown A lies 20 km north of town B. Town C lies 13 km west of town A.A small plane flies directly from town B to town C. What is the displacement of the plane ?
A33km,33∘ north of westB19km,33∘ north of westC24km,57∘ north of westD31km,57∘ north of west
A courier- person cycles from a town to a neighbouring suburban area to deliver a parcel to a merchant. His distance from the town at different times is shown by the following graph.
(a) What is the scale taken for the time axis? (b) How much time did the person take for the travel? (c) How far is the place of the merchant from the town? (d) Did the person stop on his way? Explain. (e) During which period did he ride fastest?
View SolutionWho did Valli find in her home when she returned from the town ?
View SolutionTown D is towards East of town F. Town B is towards North of town D. Town H is towards South of town B. Towards which direction is town H from F?
View SolutionAn aeroplane flies along a straight line from A to B with a speed v0. A steady wind v is blowing if AB=l then
a)total time for the trip is 2v0lv20−v2 if wind blows along the line AB
b)total time for the trip is 2l√v20−v2,if wind blows perpendicular to the line AB
c)total time for the trip decrease because of the pressure of wind
d)total time for the trip increase because of the presence of wind
View SolutionTown D is towards the East of town A at 13 km. A bus starts from town A, travels 8 km towards West and takes a right turn . After taking the right turn, it travels 5 km and reaches town B. From town B the bus takes a right turn again, travels 21 km and stops. How far and towards which direction must the bus travel to reach town D ?
View Solution
