An object has velocity w.r.t. ground. An observer moving with constant velocity w.r.t. ground measures the velocity of the object as . The magnitudes of three velocities are related by
All of the above
The correct Answer is:D
By definition of relative velocity
will be sides of a triangle and we know that the sum of any two sides is greater than third sides of the triangle.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:DISHA PUBLICATIONChapter:MOTION IN A STRAIGHT LINEExercise:Exercise-2
Explore 30 Videos
- MOTION IN A STRAIGHT LINEBook:DISHA PUBLICATIONChapter:MOTION IN A STRAIGHT LINEExercise:Exercise-2
Explore 30 Videos
- MOTION IN A PLANE Book:DISHA PUBLICATIONChapter:MOTION IN A PLANE Exercise:Exercise -2 : CONCEPT APPLICATOR
Explore 28 Videos
- MOVING CHARGES AND MAGNETISM Book:DISHA PUBLICATIONChapter:MOVING CHARGES AND MAGNETISM Exercise:EXERCISE - 2 : Concept Applicator
Explore 25 Videos
Similar Questions
Knowledge Check
The velocity of image w.r.t ground in the below figure is
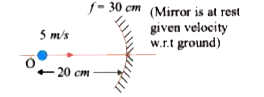 A45 m/s and approaches the mirrorB45 m/s and moves away from the mirrorC60 m/s and approaches the mirrorD60 m/s and moves away from the mirror
A45 m/s and approaches the mirrorB45 m/s and moves away from the mirrorC60 m/s and approaches the mirrorD60 m/s and moves away from the mirrorA particle moving with velocity →V is acted by the three forces shown by the vector triangle PQR. The velocity of the particle will :
 AIncreaseBDecreaseCRemain constantDChange according to the smallest force
AIncreaseBDecreaseCRemain constantDChange according to the smallest forceA bird is flying towards south with a velocity 40km/h and a train is moving with a velocity 40 km/h towards east. What is the velocity of the bird w.r.t. an obserber in the train ?
A40√2km/h. N-EB40√2km/h. S-EC40√2 km/h. S-WD40√2 km/h. N-W
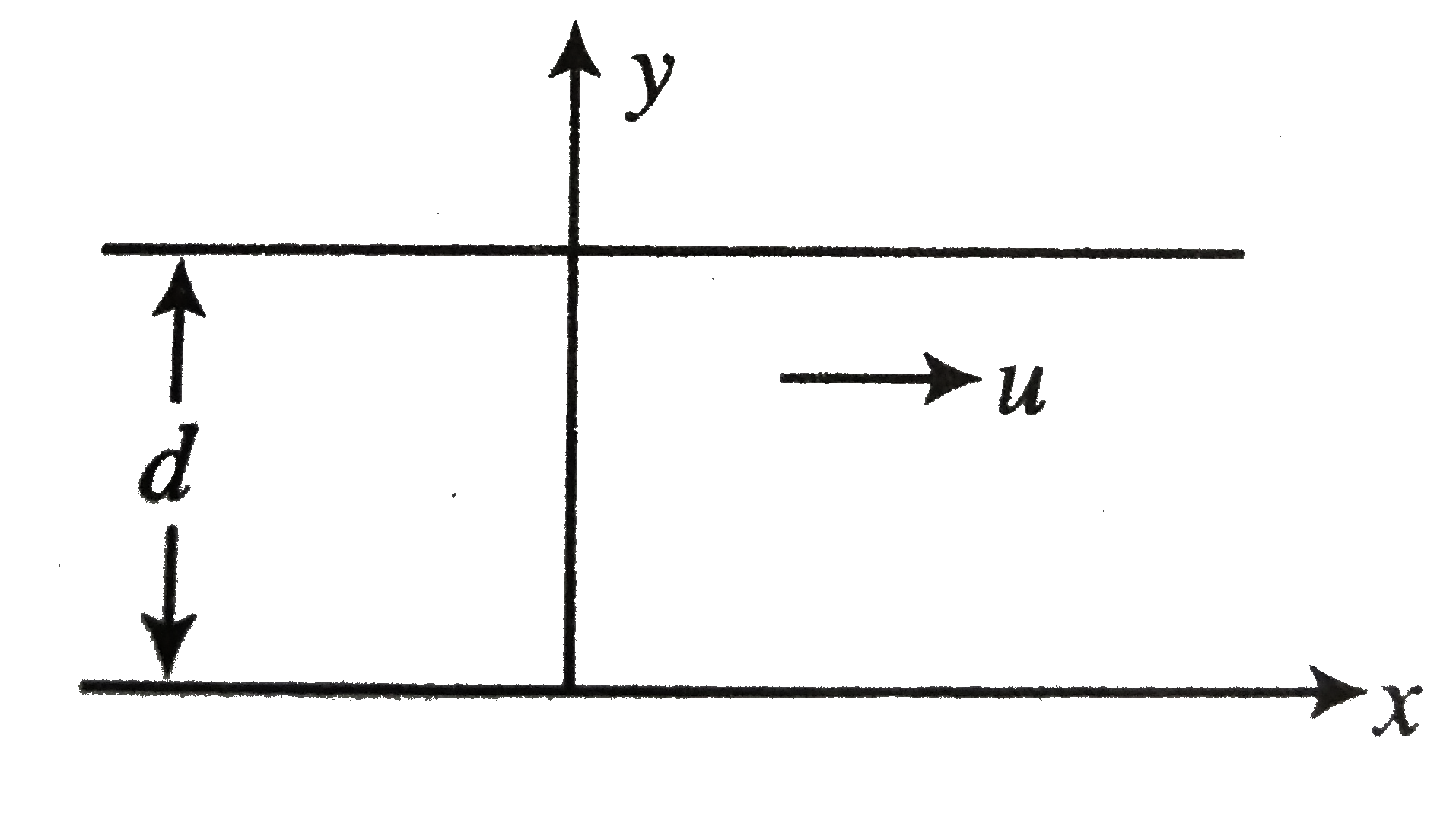
We know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.
View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.
View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.
View SolutionTwo objects A and B are moving in opposite directions with velocities vAandvB respectively, the magnitude of relative velocity of A w.r.t. B is
View SolutionThe velocity varies with time as →v=aˆi+btˆj , where a and b are positive constants. The magnitude of instantaneous velocity and acceleration would be
View Solution