Two particles A and B are thrown vertically upward with velocity, 5ms−1 and 10ms−1 respectively (g=10ms−2), Find separation between them after 1s.
 .
.
SA=ut−12gt2=5t−12×10×t2=5×1−5×12=5−5=0
SB=ut−12gt2=10×1−12×10×12=10−5=5
∴SB−SA=separation=5m.
Similar Questions
Two particles A and B are thown vertically upward with velocity, vertically upward with velocity, 5ms−1 and 10ms−1 respectively (g=10 m s^(-2)), Find separation between them after 1s.
 .
.
View SolutionA and B are thrown vertivally upward with velocity 5m/s and 10 m/s respectively (g=10m/s2 ) . Find separtion between them after one second .
View Solution
Knowledge Check
Light travels in two media A and B with speeds 1.8×108ms–1and2.4×108ms–1 respectively. Then the critical angle between them is
Asin−1(23)Btan−1(34)Ctan−1(23)Dsin−1(34)
A pebble thrown vertically upwards with an initial velocity 50 m s−1 comes to a stop in 5 s. Find the retardation.
View SolutionTwo particles are located on a horizontal plane at a distance 60m. At t=0 both the particles are simultaneously projected at angle 45∘ with velocities 2ms−1and14ms−1, respectively. Find
(a) Minimum separation between them during motion.
(b) At what time is the separation between them minimum ?
 .
.
View SolutionA pebble is thrown vertically upwards with a speed of 20 m s−1. How high will it be after 2 s? (Take g = 10 m s−2)
View SolutionAn object is thrwon vertically upwards with a velocity of 60 m/s. After what time it strike the ground ? Use g=10m/s2.
View SolutionTwo particles are simultaneously thrown from the top of two towards as shown. Their velocities are 2ms−1and14ms−1. Horizontal and vertical separations between these particles are 22 m and 9 m respectively. Then the minimum separation between the particles in the process of their motion in meters is (g=10ms−2)
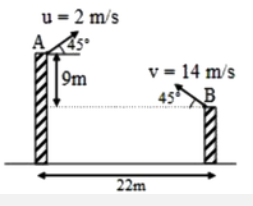
View SolutionFind the maximum height reached by a particle which is thrown vertically upwards with the velocity of 20m/s (take g=10m/s2).
View SolutionA particle is thrown vertically upward. Its velocity at half of the height is 10 m/s. Then the maximum height attained by it : -
(g=10m/s2)
View Solution
