The acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity?
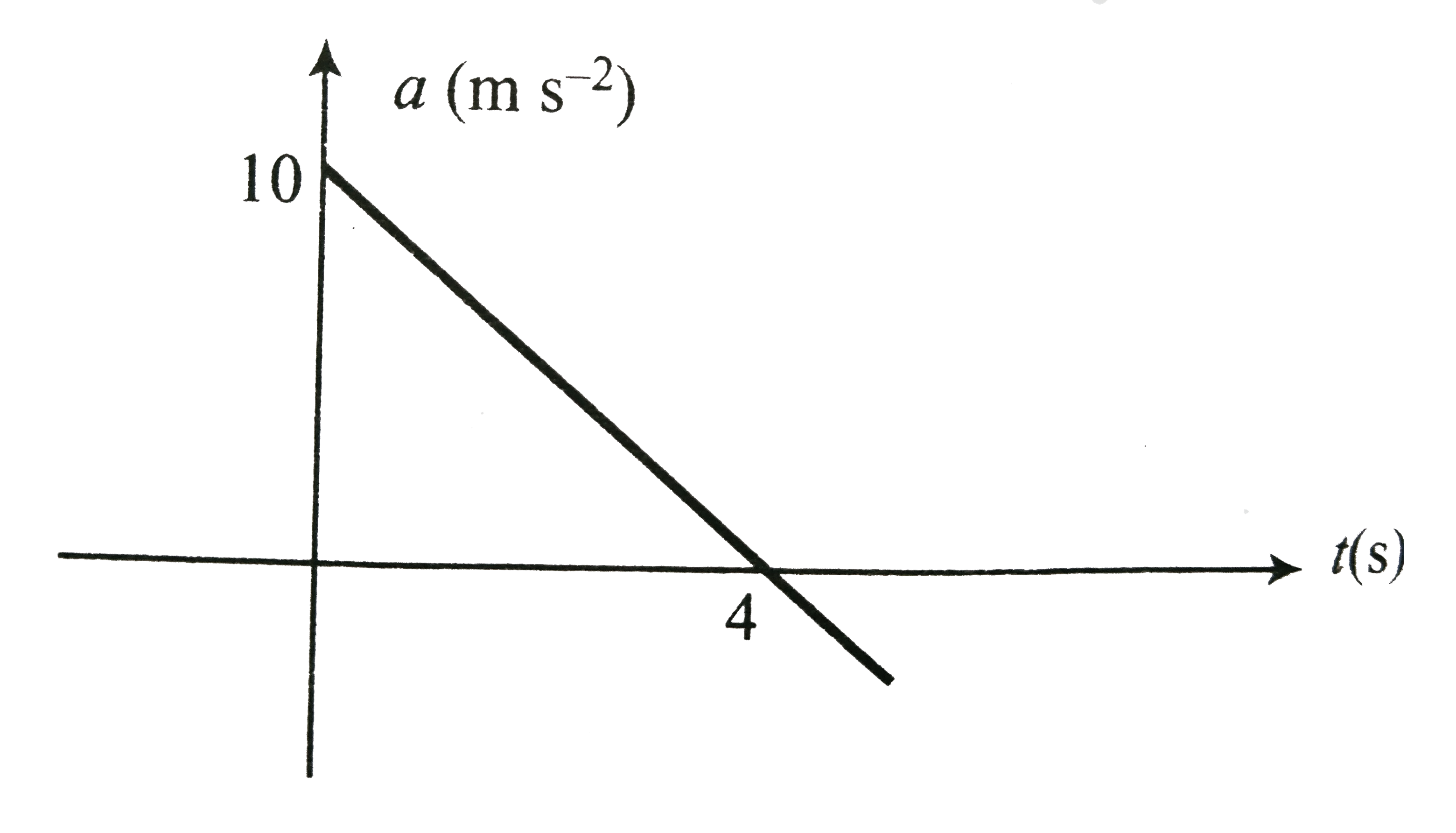 .
.
(3−√3)S
(2+√3)S
(2−√5)S
(2+√5)S
The correct Answer is:B
Step by step video solution for The acceleration-time graph of a particle moving along a straight line is as shown in. At what time the particle acquires its initial velocity? . by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Figure shows the acceleration-time graph of a particle moving along a straight line. After what time the particle acquires its initial velocity?

View SolutionDisplacement time graph of a particle moving in a straight line is a shown in figure.
View SolutionThe variation of velocity of a particle moving along a straight line is shown in . is
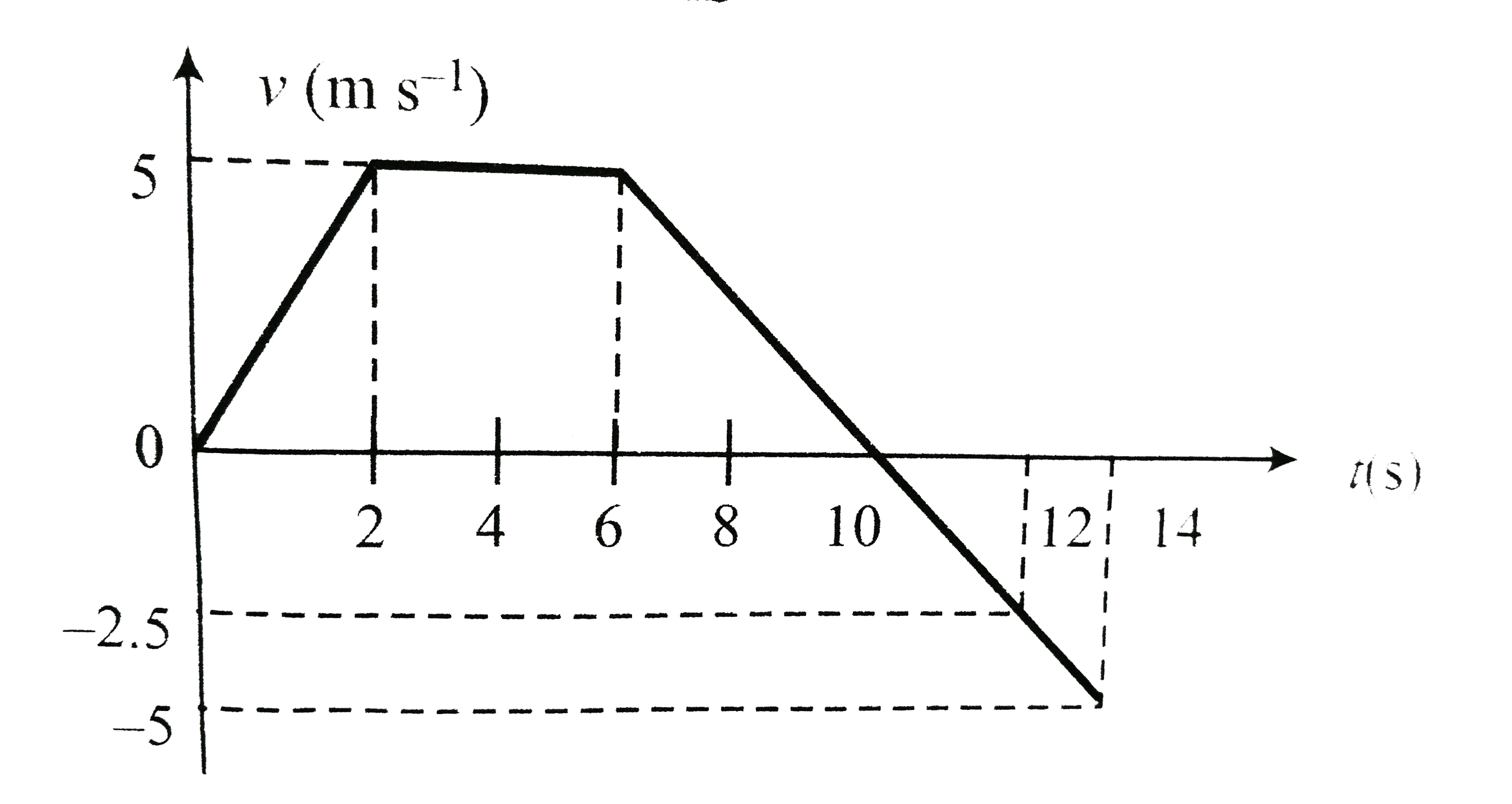 .
.
View SolutionVelocity displacement graph of a particle moving in a straight line is as shown in figure.
View SolutionThe acceleration-time graph of a particle moving in a straight line is as shown in figure. The velocity of the particle at time t=0 is 2m/s. The velocity after 2 seconds will be

View SolutionThe acceleration-time graph of a particle moving in a straight line is as shown in figure. The velocity of the particle at time t=0 is 2m/s. The velocity after 2 seconds will be

View SolutionThe acceleration versus time graph for a particle moving along a straight line is shown in the figure. If the particle starts from rest at t = 0, then its speed at t = 30 sec will be :
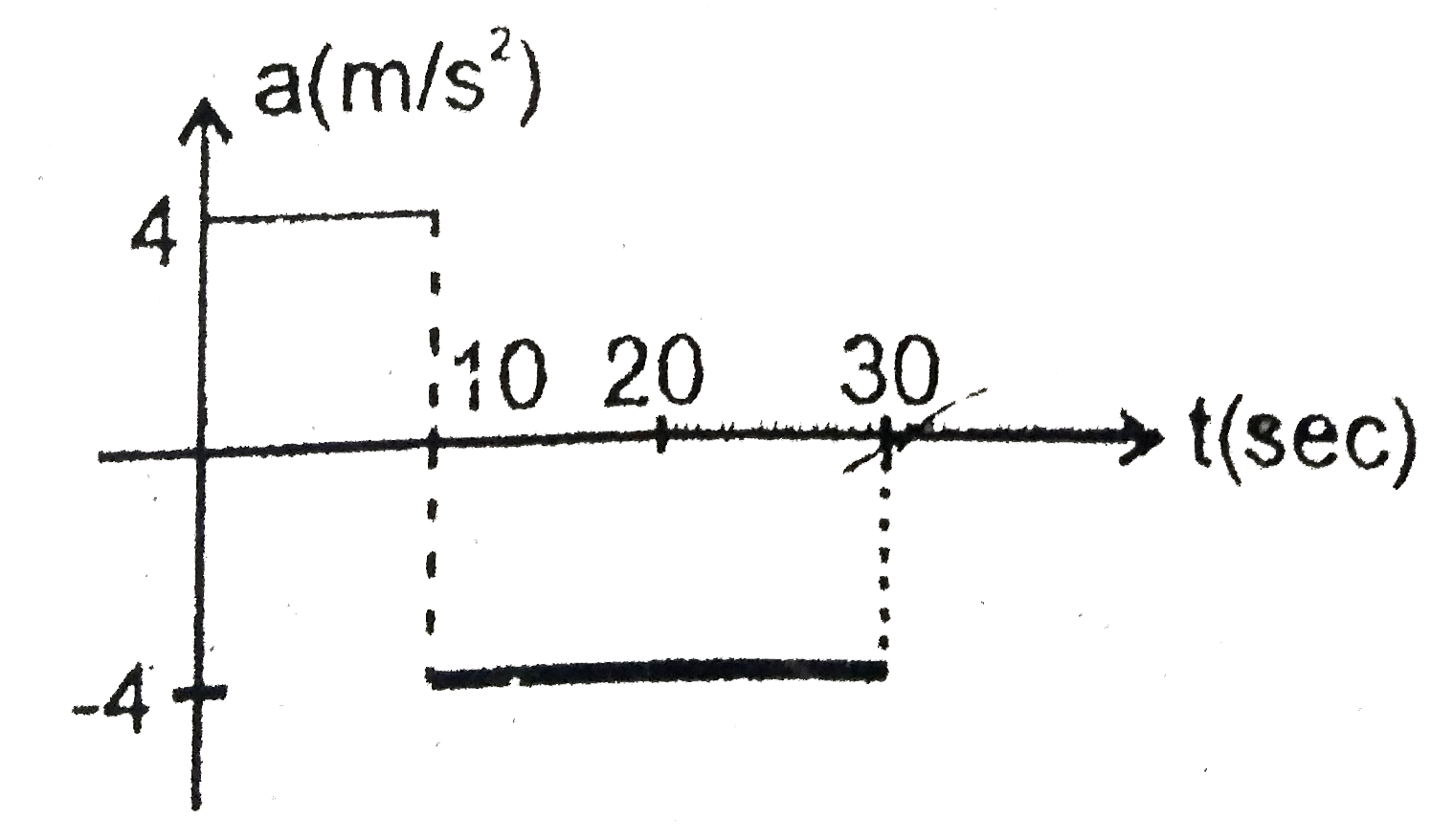
View SolutionThe acceleration-time (a−t) graph of a particle moving along straight line is as shown in figure. The time at which velocity of particle becomes equal to its initial velocity is

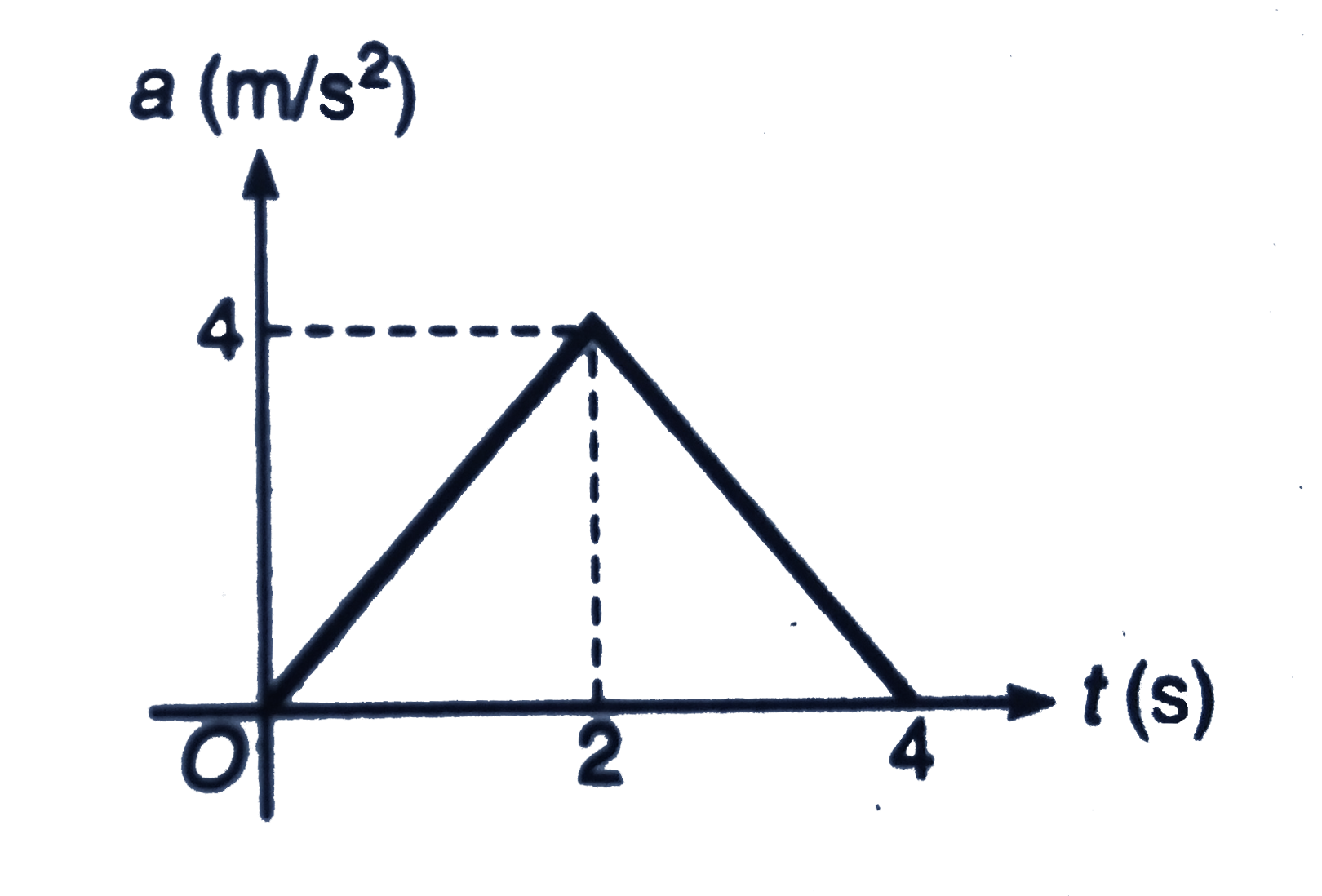
View SolutionAccleration-time graph of a particle moving in a straight line is as shown in Fig. Velocity of particle at time t=0 is 2m/s. Find the velocity at the end of fourth second.
View SolutionThe acceleration versus time graph of a particle moving in a straight line is show in. The velocity-time graph of the particle would be
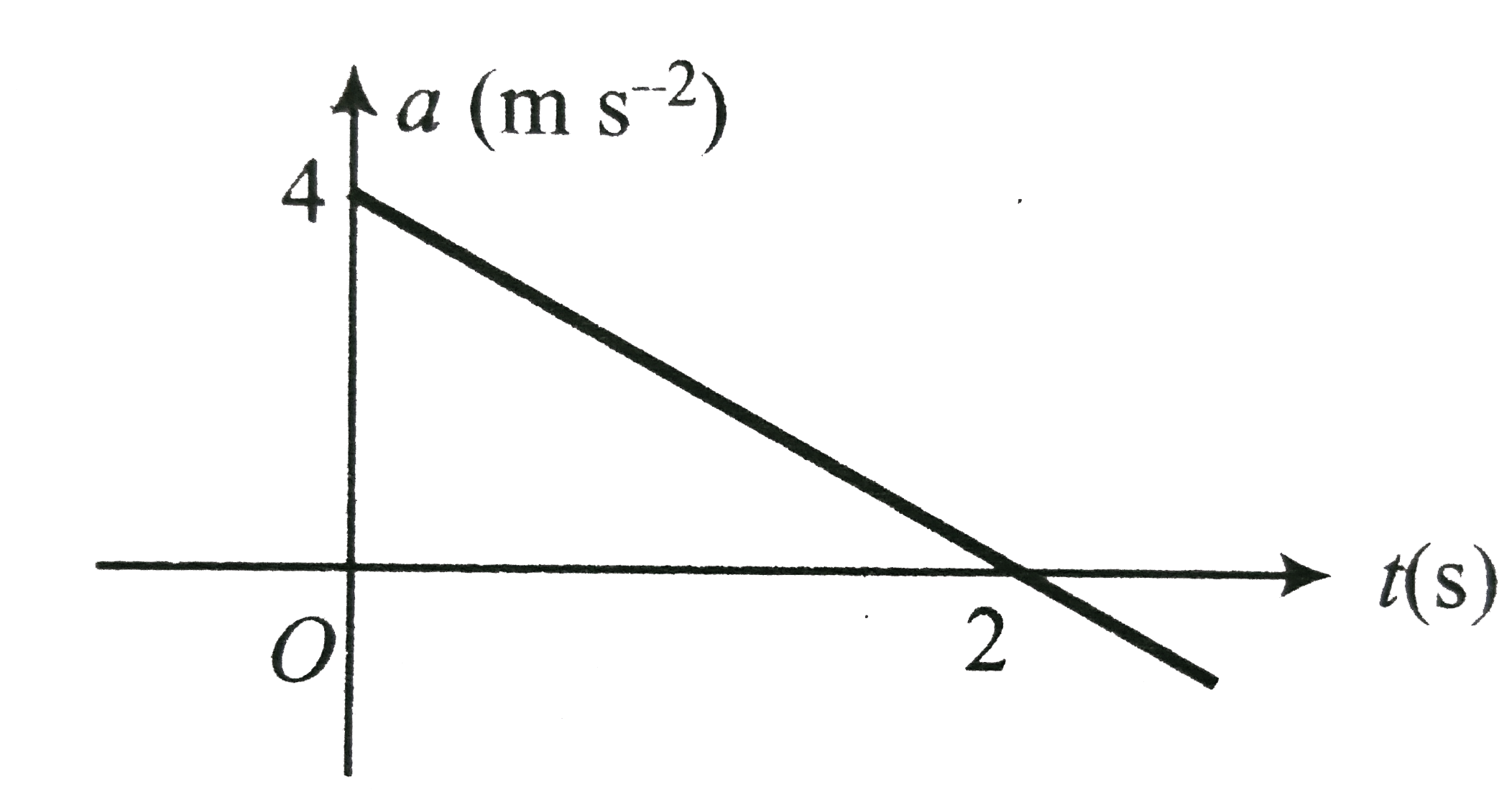 .
.
View Solution
