The distance between two moving particles at any time is a. If be their relative velocity and and be the components of along and perpendicular to a. The time when they are closest to each other is
The correct Answer is:A
To solve the problem step by step, we will analyze the situation involving two moving particles and their relative motion.
Step 1: Understand the Problem
We have two particles moving such that the distance between them at any time is A. The relative velocity v is given, and we need to find the time when they are closest to each other. The components of the relative velocity are v1 (along the line connecting the two particles) and v2 (perpendicular to that line).
Hint: Visualize the situation by drawing a diagram of the two particles and the vectors representing their velocities.
Step 2: Identify the Components of Relative Velocity
The relative velocity v can be broken down into two components:
- v1: the component of the relative velocity along the line connecting the two particles.
- v2: the component of the relative velocity perpendicular to that line.
Hint: Remember that the relative velocity can be represented as a vector triangle where v is the hypotenuse, and v1 and v2 are the two legs.
Step 3: Determine the Approaching Velocity
The component v1 is the effective velocity that brings the two particles closer together. The time T when they are closest is determined by how long it takes for the distance A to be covered at this approaching velocity v1.
Hint: The time to cover a distance can be calculated using the formula T=DistanceVelocity.
Step 4: Write the Expression for Time
Using the distance A and the approaching velocity v1, we can express the time T when the particles are closest:
T=Av1
Hint: Substitute v1 in terms of v and v2 if necessary.
Step 5: Relate v1 to v and v2
From the triangle formed by the velocities, we can relate v1 and v2 using trigonometric identities:
v1=vcos(θ)
where θ is the angle between v and v1.
Hint: Use the relationship between the components of the velocity to express v1 in terms of v and v2.
Step 6: Substitute v1 into the Time Equation
Substituting v1 into the time equation gives:
T=Avcos(θ)
Hint: Recognize that cos(θ) can be expressed as v1v.
Step 7: Final Expression for Time
After substituting and simplifying, we find:
T=Av1v2
Hint: Ensure that all terms are correctly placed and that the units are consistent.
Conclusion
The time when the two particles are closest to each other is given by:
T=Av1v22
Thus, the correct option is option 1.
We have two particles moving such that the distance between them at any time is A. The relative velocity v is given, and we need to find the time when they are closest to each other. The components of the relative velocity are v1 (along the line connecting the two particles) and v2 (perpendicular to that line).
The relative velocity v can be broken down into two components:
- v1: the component of the relative velocity along the line connecting the two particles.
- v2: the component of the relative velocity perpendicular to that line.
The component v1 is the effective velocity that brings the two particles closer together. The time T when they are closest is determined by how long it takes for the distance A to be covered at this approaching velocity v1.
Using the distance A and the approaching velocity v1, we can express the time T when the particles are closest:
T=Av1
From the triangle formed by the velocities, we can relate v1 and v2 using trigonometric identities:
v1=vcos(θ)
where θ is the angle between v and v1.
Substituting v1 into the time equation gives:
T=Avcos(θ)
After substituting and simplifying, we find:
T=Av1v2
The time when the two particles are closest to each other is given by:
T=Av1v22
Thus, the correct option is option 1.
Similar Questions
The distance between two moving particles P and Q at any time is a.If vr be their relative velocity and if u and v be the components of vr, along and perpendicular to PQ.The closest distance between P and Q and time that elapses before they arrive at their nearest distance is
View SolutionA particle move with velocity v1 for time t1andv2 for time t2 along a straight line. The magntidue of its average acceleration is
View SolutionTwo identical particles move towards each other with velocity 2v and v, respectively. The velocity of the centre of mass is:
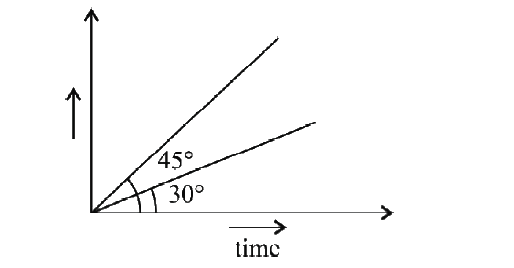
View SolutionThe displacement time graph of two moving particles make angles of 30∘ and 45∘ with the x-axis. The ratio of the two velocities VAandVB is
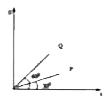
View SolutionThe displacement-time graphs of two particles P and Q are as shown in the figure. The ratio of their velocities VP and VQ will be
View SolutionA particle is moving with velocity v=100ms−1. If one of the rectangular components of a velocity is 50ms−1. Find the other component of velocity and its angle with the given component of velocity.
View SolutionTwo particles move in a uniform gravitational field with an acceleration g. At the intial moment the particles were located at one point and moved with velocity v1=1 ms−1 and v2=4 ms−1 horizontally in opposite directions. Find the time interval after their velocity vectors become mutually perpendicular
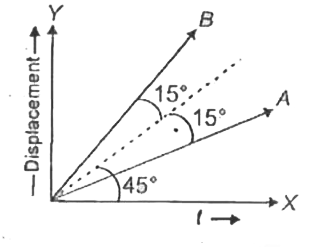
View SolutionThe displacement - time graph for two particles A and B is as follows. The ratio vAvB is
View SolutionTwo particles are moving with velocities v1andv2 . Their relative velocity is the maximum, when the angle between their velocities is
View SolutionA particle travels along a straight line. It covers halg the distance with a speed (v). The remaining part of the distance was covere with speed v1 for half the time and with speed v2 for the other half the time . Find the average speed of the particle over the entire motion.
View Solution