A particle is moving with velocity v=100ms−1. If one of the rectangular components of a velocity is 50ms−1. Find the other component of velocity and its angle with the given component of velocity.
To solve the problem step by step, we will use the Pythagorean theorem and trigonometric relationships.
Step 1: Understand the components of velocity
The velocity of the particle is given as v=100m/s. One of the rectangular components of this velocity is given as vx=50m/s. We need to find the other component of velocity, which we will denote as vy.
Step 2: Apply the Pythagorean theorem
Since the components of velocity are perpendicular to each other, we can use the Pythagorean theorem:
v2=v2x+v2y
Substituting the known values:
1002=502+v2y
This simplifies to:
10000=2500+v2y
Step 3: Solve for v2y
Rearranging the equation to isolate v2y:
v2y=10000−2500
v2y=7500
Step 4: Calculate vy
Taking the square root of both sides to find vy:
vy=√7500≈86.6m/s
Step 5: Find the angle with respect to the given component
Let’s denote the angle between the velocity vector and the component vx as θ. We can use the sine function to find this angle:
sinθ=vxv=50100=0.5
Step 6: Determine the angle θ
From trigonometric values, we know:
sin30∘=0.5
Thus, we find:
θ=30∘
Final Answers:
1. The other component of velocity vy is approximately 86.6m/s.
2. The angle θ with respect to the given component vx is 30∘.
---
The velocity of the particle is given as v=100m/s. One of the rectangular components of this velocity is given as vx=50m/s. We need to find the other component of velocity, which we will denote as vy.
Since the components of velocity are perpendicular to each other, we can use the Pythagorean theorem:
v2=v2x+v2y
Substituting the known values:
1002=502+v2y
This simplifies to:
10000=2500+v2y
Rearranging the equation to isolate v2y:
v2y=10000−2500
v2y=7500
Taking the square root of both sides to find vy:
vy=√7500≈86.6m/s
Let’s denote the angle between the velocity vector and the component vx as θ. We can use the sine function to find this angle:
sinθ=vxv=50100=0.5
From trigonometric values, we know:
sin30∘=0.5
Thus, we find:
θ=30∘
1. The other component of velocity vy is approximately 86.6m/s.
2. The angle θ with respect to the given component vx is 30∘.
Topper's Solved these Questions
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise 3.1
Explore 19 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise 3.2
Explore 13 Videos
- TRAVELLING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:TRAVELLING WAVESExercise:Integer
Explore 9 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Archives (integer)
Explore 4 Videos
Similar Questions
One of the rectangular components of a velocity of 20 ms−1 is 10 ms−1. Find the other component.
View SolutionA particle moves in a circle of radius 4 m with a linear velocity of 20ms−1. Find the angular velocity.
View SolutionA particle has a displacement of 8 m . If one of its rectangular components is 4 m what is the other rectangular component ?
View SolutionAn uniform electric field of strength E exists in a region. An electron of mass m enters a point A perpendicular to x - axis with velocity V. It moves through the electric field and exists at point B. The components of velocity at B are shown in (Fig. 3.156). At B the y - component of velocity remain uncharged.
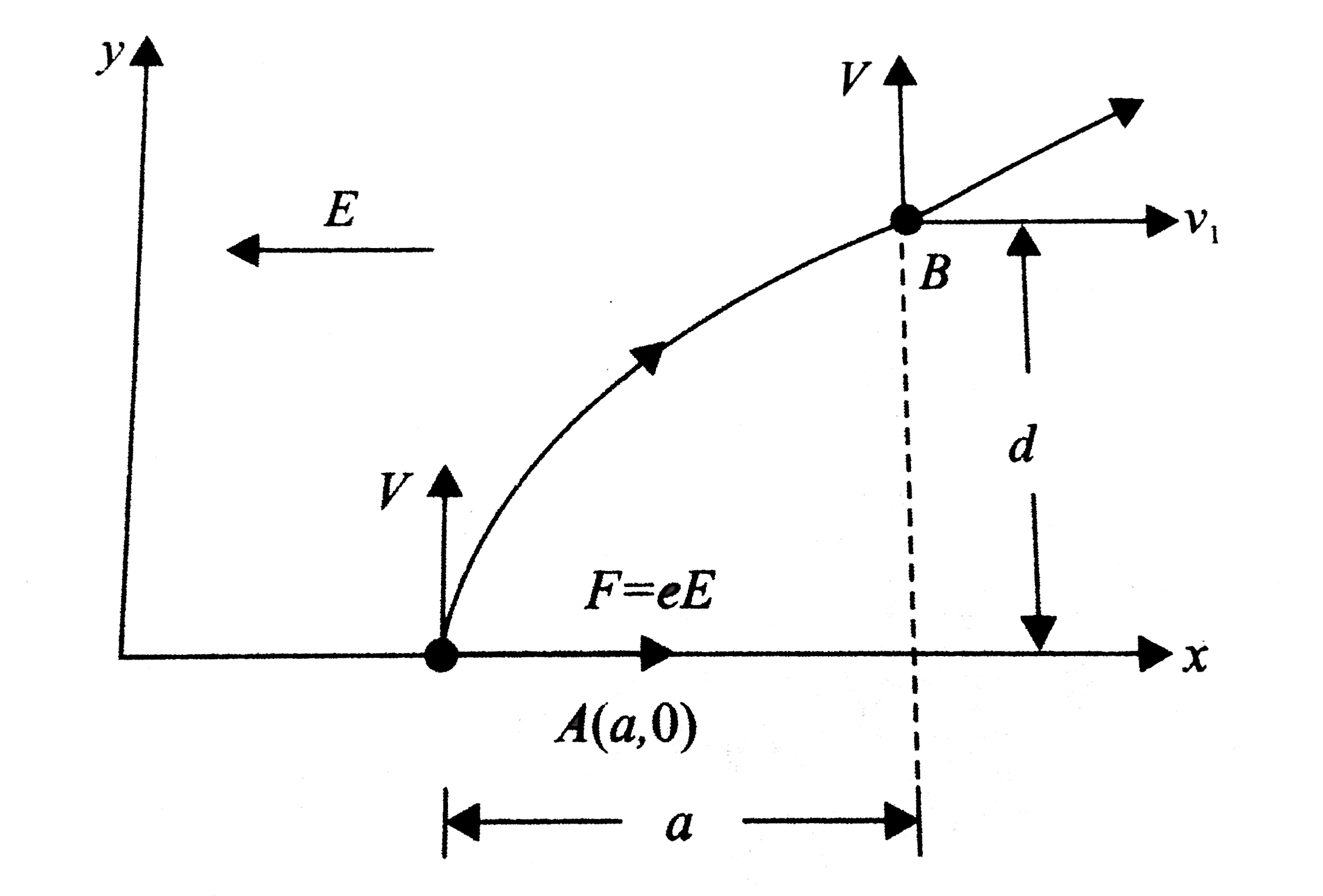 .
.
Find velocity at B.
View SolutionThe projectile has only vertical component of velocity at the highest point of its trajectory.
At the highest point, only one component of velocity is present.
View SolutionAn uniform electric field of strength E exists in a region. An electron of mass m enters a point A perpendicular to x - axis with velocity V. It moves through the electric field and exists at point B. The components of velocity at B are shown in (Fig. 3.156). At B the y - component of velocity remain uncharged.
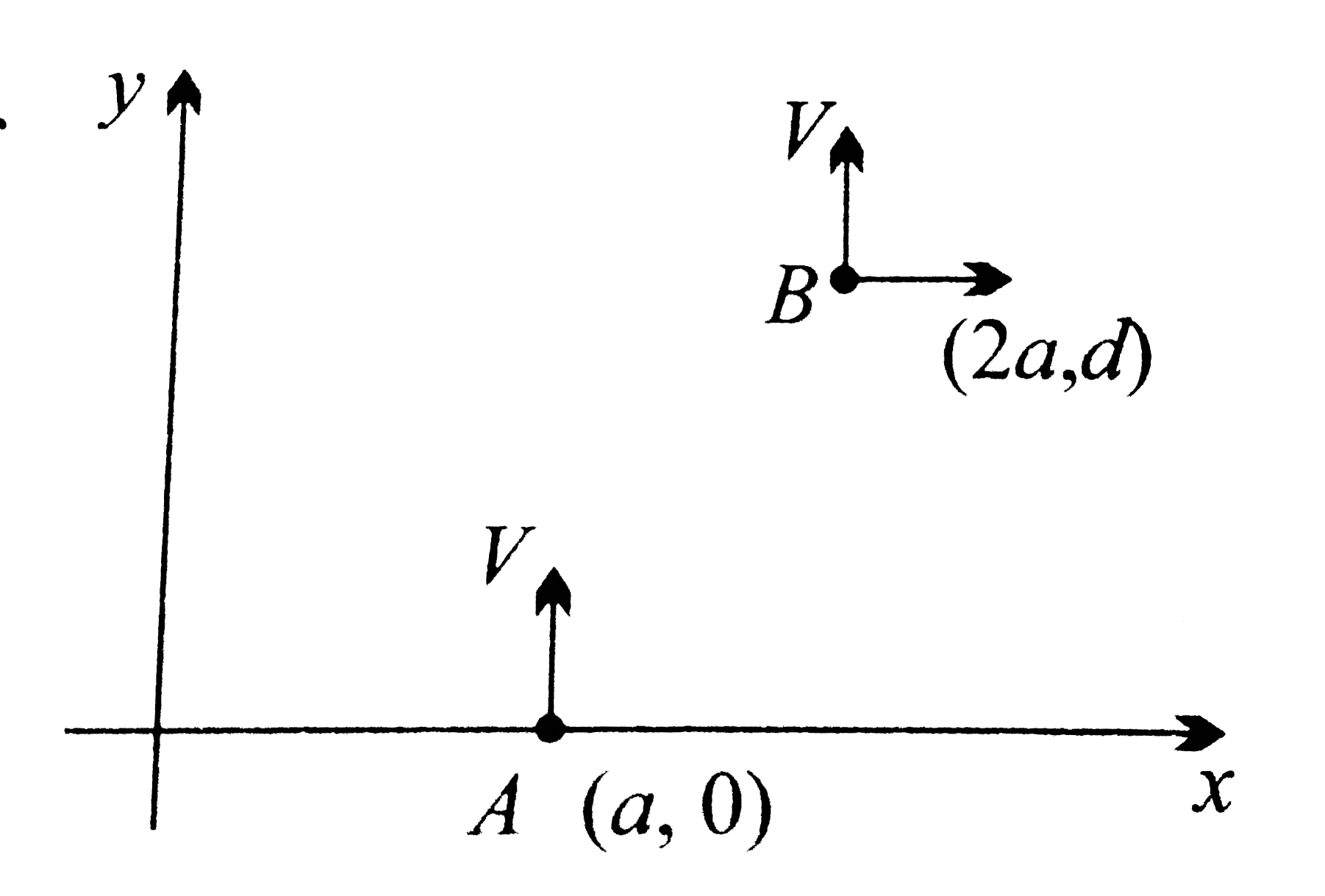 .
.
Find electric field.
View Solutiony component of velocity is 20andx component of velocity is 10. The direction of motion of the body with the horizonatal at this instant is
View SolutionA body is thrown into air with a velocity 5 m/s making an angle 30∘ with the horizontal .If the vertical component of the velocity is 5 m/s what is the velocity of the body ? Also find the horizontal component .
View SolutionA body is projected horizontally from the top of a tower with a velocity of 20 m/s. After what time the vertical component of velocity is four times the horizontal component of velocity ? (g = 10m/s2)
View SolutionA car travels a distance 100 m with a constant acceleration and average velocity of 20 m s−1 . The final velocity acquired by the car is 25 m s−1. Find : (i) the initial velocity and (ii) acceleration of car.
View Solution