Two vectors →Aand→B lie in plane, another vector →C lies outside this plane, then the resultant of these three vectors i.e., →A+→B+→C
cannot be zero
can be zero
Lies in the plane of →A or →B
Lies in a plane different from that of any of the three vectors
The correct Answer is:A, D
To solve the problem of determining the resultant of the vectors →A, →B, and →C, we will follow these steps:
Step 1: Understand the Configuration of the Vectors
- Vectors →A and →B lie in a plane, which we can denote as the XY-plane.
- Vector →C lies outside this plane, which can be represented as being along the Z-axis (perpendicular to the XY-plane).
Hint: Visualize the vectors in a 3D coordinate system to understand their orientation.
Step 2: Analyze the Resultant of Vectors →A and →B
- The resultant vector of →A and →B can be denoted as →R=→A+→B.
- Since both →A and →B lie in the same plane (XY-plane), the resultant →R will also lie in the same plane.
Hint: Remember that the resultant of two vectors in the same plane will always remain in that plane.
Step 3: Consider the Effect of Vector →C
- Vector →C lies outside the plane of →A and →B. This means that →C has a component that is perpendicular to the plane formed by →A and →B.
- The resultant vector of →A, →B, and →C can be expressed as →Rtotal=→R+→C.
Hint: Think about how adding a vector that is perpendicular to the plane affects the overall direction of the resultant vector.
Step 4: Determine if the Resultant Can Be Zero
- Since →R lies in the XY-plane and →C lies along the Z-axis, they cannot cancel each other out.
- The components of →R cannot counteract the component of →C that is perpendicular to the XY-plane.
Hint: Recall that for two vectors to sum to zero, they must be equal in magnitude and opposite in direction.
Step 5: Conclusion
- Therefore, the resultant of the three vectors →A+→B+→C cannot be zero because →C introduces a component that is outside the plane of →A and →B.
- Thus, we conclude that the sum of these three vectors cannot be zero.
Final Answer: The resultant of the vectors →A+→B+→C is not zero.
- Vectors →A and →B lie in a plane, which we can denote as the XY-plane.
- Vector →C lies outside this plane, which can be represented as being along the Z-axis (perpendicular to the XY-plane).
- The resultant vector of →A and →B can be denoted as →R=→A+→B.
- Since both →A and →B lie in the same plane (XY-plane), the resultant →R will also lie in the same plane.
- Vector →C lies outside the plane of →A and →B. This means that →C has a component that is perpendicular to the plane formed by →A and →B.
- The resultant vector of →A, →B, and →C can be expressed as →Rtotal=→R+→C.
- Since →R lies in the XY-plane and →C lies along the Z-axis, they cannot cancel each other out.
- The components of →R cannot counteract the component of →C that is perpendicular to the XY-plane.
- Therefore, the resultant of the three vectors →A+→B+→C cannot be zero because →C introduces a component that is outside the plane of →A and →B.
- Thus, we conclude that the sum of these three vectors cannot be zero.
Topper's Solved these Questions
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Single Correct
51 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Integer
9 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos
Similar Questions
Knowledge Check
If →a,→b and →c are unit vectors such that→a+→b+→c=0, then the values of →a.→b+→b.→c+→c.→a is
A1B32C−32Dnone of these
The resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is

View SolutionIf the vectors →a+→b,→b+→c and →c+→a are coplanar, then prove that the vectors →a,→b and →c are also coplanar.
View SolutionIf →A,→B and →C are three vectors, then the wrong relation is :
View SolutionKeeping one vector constant, if direction of other to be added in the first vector is changed continuously, tip of the resultant vector describes a circles, In the following figure vector →a is kept constant. When vector →b addede to →a changes its direction, the tip of the resultant vector →r=→a+→b describes circles of radius b with its centre at the tip of vector →a. Maximum angle between vector →a and the resultant →r=→a+→b is
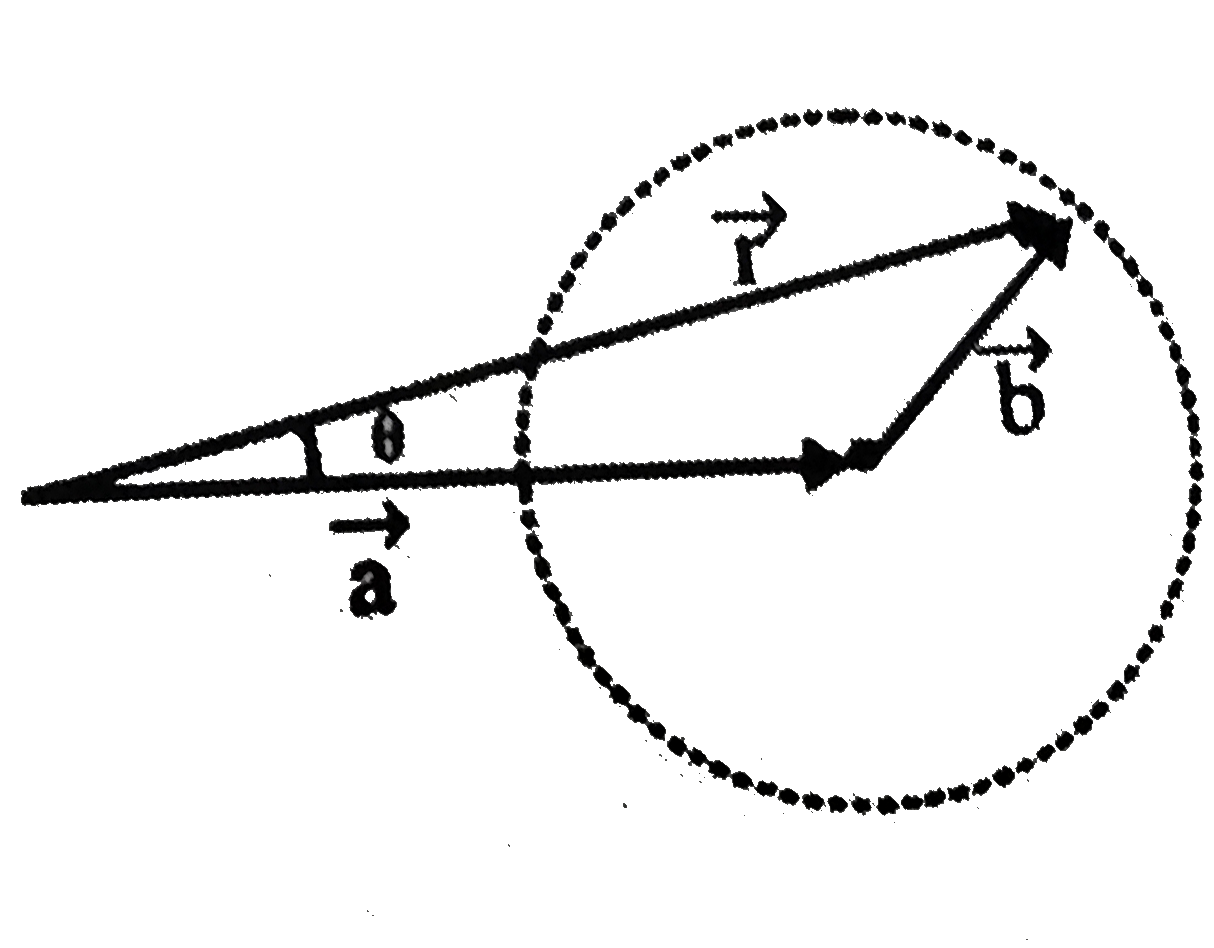
View SolutionIf two vectors →aand→b are such that ∣∣→a.→b∣∣=∣∣→a×→b∣∣, then find the angle the vectors →aand→b
View SolutionFor two vectors →A and →B
∣∣→A+→B∣∣=∣∣→A−→B∣∣ is always true when.
View SolutionIf →a,→b,and→c are non-zero vectors such that →a.→b=→a.→c, then find the geometrical relation between the vectors.
View Solution
