Let I1andI2 be the moments of inertia of two bodies of identical geometrical shape, the first made of aluminum and the second of iron.
I1<I2
I1=I2
I1>I2
relatioan between I1 and I2 depends on the actual shapes of the bodies
The correct Answer is:A
Step by step video solution for Let I_1 and I_2 be the moments of inertia of two bodies of identical geometrical shape, the first made of aluminum and the second of iron. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Statement - 1 : Let I1andI2 be the moment of inertia of two bodies of identical geometrical shapes, the first made of aluminium and second of iron then I1<I2. Becaause
Statement - 2 : Moment of inertia does not depends on shape
View SolutionThe moment of inertia of a ring about its geometrical axis is I, then its moment of inertia about its diameter will be
View Solution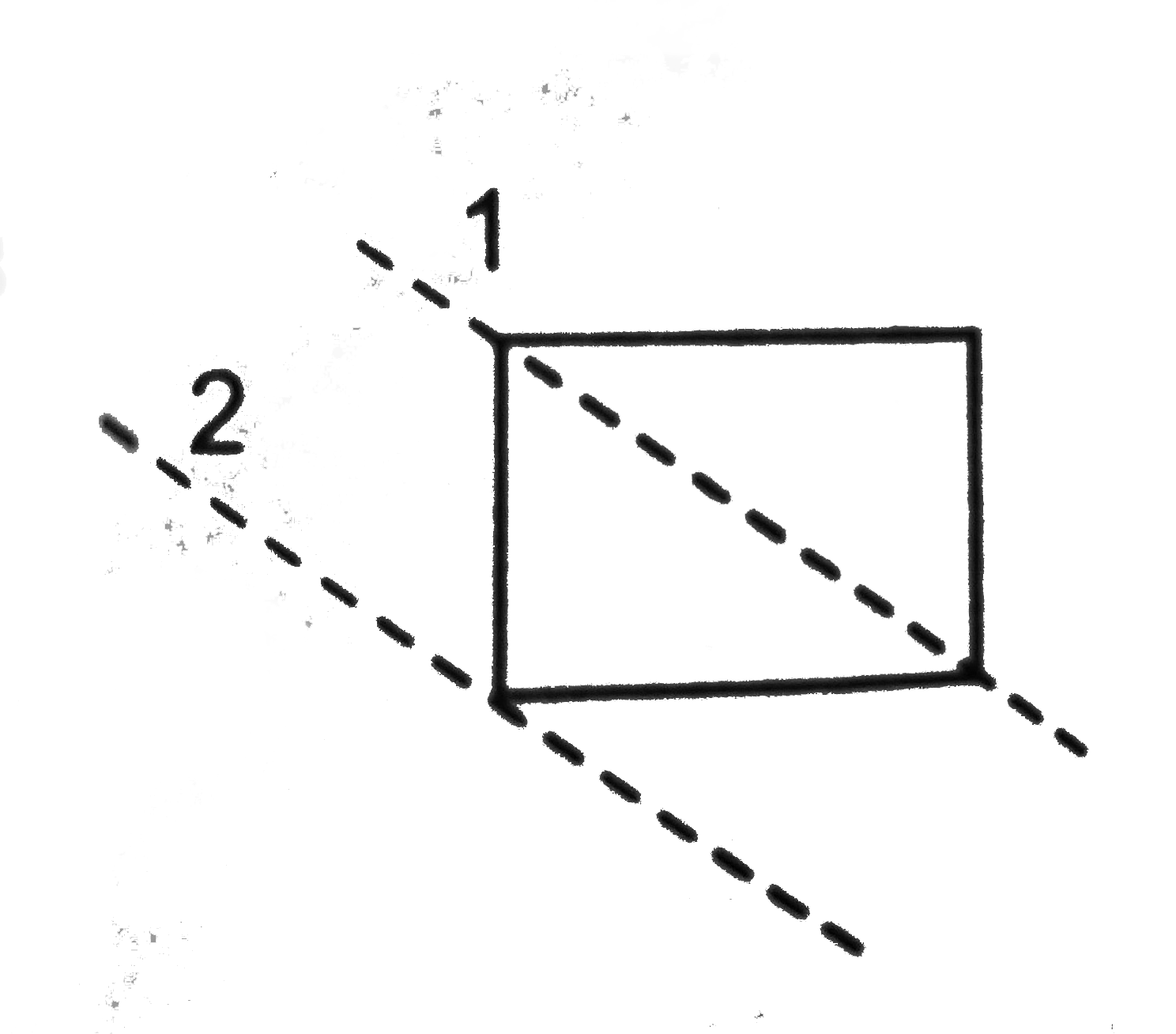
Let I1 and I2 be the moment of inertia of a uniform square plate about axes shown in the figure. Then the ratio I1:I2 is
View SolutionLet IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not. Then
View SolutionLet IAandIB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of massof the body but B does not. Choose the correct option.
View SolutionA rigid body is rotating about a vertical axis. In t second, the axis gradually becomes horizontal. But the rigid body continues to make v rotations per second throughout the time interval of 1 second. If the moment of inertia I of the body about the axis of rotation can he taken as constant, then the torque acting on the body is
View SolutionIf I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 is the moment of inertia of the ring about an axis perpendicular to plane of ring and passing through its centre formed by bending the rod, then
View SolutionTwo discs A and B have same mass and same thickness. If d1 and d2 are the densities of the materials of the discs A and B respectively, then the ratio of the moment of inertia of the discs A and B about their geometrical axis is
View SolutionA semi-circular ring has mass m and radius R as shown in figure. Let I1,I2,I3 and I4 be the moments of inertia about the four axes as shown . Axis 1 passes through centre and is perpendicular to plane of ring. Then , match the following.
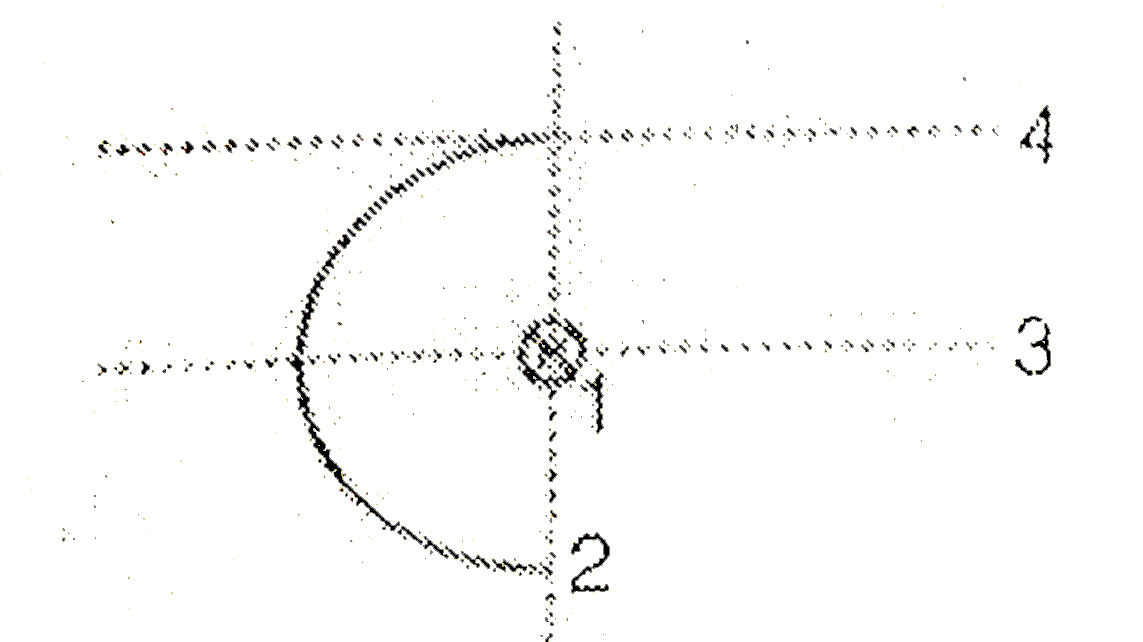

View SolutionIf I1,I2 and I3 are the moments of inertia about the natural axies of solid sphere, hollow sphere and a spherical shell of same mass and radii, the correct result of the following is
View Solution
