Statement - 1 : Let I1andI2 be the moment of inertia of two bodies of identical geometrical shapes, the first made of aluminium and second of iron then I1<I2. Becaause
Statement - 2 : Moment of inertia does not depends on shape
Statement - 1 is true, statement - 2 is true, statement - 2 is correct explanation for statement - 1
Statement - 1 is true, Statement - 2 is true, Statement - 2 is not a correct explanation for statement - 1
statement - 1 is true, statement - 2 is false
statement - 1 is false, statement - 2 is true.
The correct Answer is:C
To analyze the statements given in the question, we will break down the reasoning step by step.
Step 1: Understanding Moment of Inertia
The moment of inertia (I) of a body is defined as the sum of the products of the mass of each particle of the body and the square of its distance from the axis of rotation. The formula can be expressed as:
I=∑mir2i
where mi is the mass of each particle and ri is the distance from the axis of rotation.
Step 2: Analyzing Statement 1
Statement 1 claims that the moment of inertia I1 of the aluminum body is less than the moment of inertia I2 of the iron body, i.e., I1<I2.
- Both bodies are of identical geometrical shapes, meaning they have the same dimensions.
- The moment of inertia depends on both the mass and the distribution of mass relative to the axis of rotation.
- Since aluminum has a lower density than iron, for the same volume (and hence the same shape), the mass of the aluminum body will be less than that of the iron body.
- Therefore, since I is directly proportional to mass (for identical shapes), we conclude that:
I1<I2
Thus, Statement 1 is true.
Step 3: Analyzing Statement 2
Statement 2 claims that the moment of inertia does not depend on shape.
- This statement is incorrect. The moment of inertia does depend on the shape of the object because it is influenced by how the mass is distributed relative to the axis of rotation.
- Different shapes (e.g., a solid cylinder vs. a hollow cylinder) will have different moments of inertia even if they have the same mass and radius.
- Therefore, Statement 2 is false.
Conclusion
- Statement 1 is true: I1<I2 because the mass of the aluminum body is less than that of the iron body.
- Statement 2 is false: The moment of inertia does depend on the shape of the object.
Final Answer
The correct option is that Statement 1 is true and Statement 2 is false.
The moment of inertia (I) of a body is defined as the sum of the products of the mass of each particle of the body and the square of its distance from the axis of rotation. The formula can be expressed as:
I=∑mir2i
where mi is the mass of each particle and ri is the distance from the axis of rotation.
Statement 1 claims that the moment of inertia I1 of the aluminum body is less than the moment of inertia I2 of the iron body, i.e., I1<I2.
- The moment of inertia depends on both the mass and the distribution of mass relative to the axis of rotation.
- Since aluminum has a lower density than iron, for the same volume (and hence the same shape), the mass of the aluminum body will be less than that of the iron body.
- Therefore, since I is directly proportional to mass (for identical shapes), we conclude that:
I1<I2
Thus, Statement 1 is true.
Statement 2 claims that the moment of inertia does not depend on shape.
- Different shapes (e.g., a solid cylinder vs. a hollow cylinder) will have different moments of inertia even if they have the same mass and radius.
- Therefore, Statement 2 is false.
- Statement 1 is true: I1<I2 because the mass of the aluminum body is less than that of the iron body.
- Statement 2 is false: The moment of inertia does depend on the shape of the object.
The correct option is that Statement 1 is true and Statement 2 is false.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - COMPREHENSION I
3 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - COMPREHENSION II
2 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - SOLVED PROBLEMS (OBJECTIVE)
14 Videos
- PHYSICS PART2BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Numerical Based Question Decimal Type
6 Videos
- SEMICONDUCTOR AND DEVICEBOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I
20 Videos
Similar Questions
If I1,I2 ,and I3 are moments of inertia of a disc about its geometric axis,diameter and a tangent in its plane,then
View SolutionLet I1 and I2 be the moment of inertia of a uniform square plate about axes APC and OPO respectively as shown in the figure.P is centre of square. The ratio I1I2 moment of inertia is -
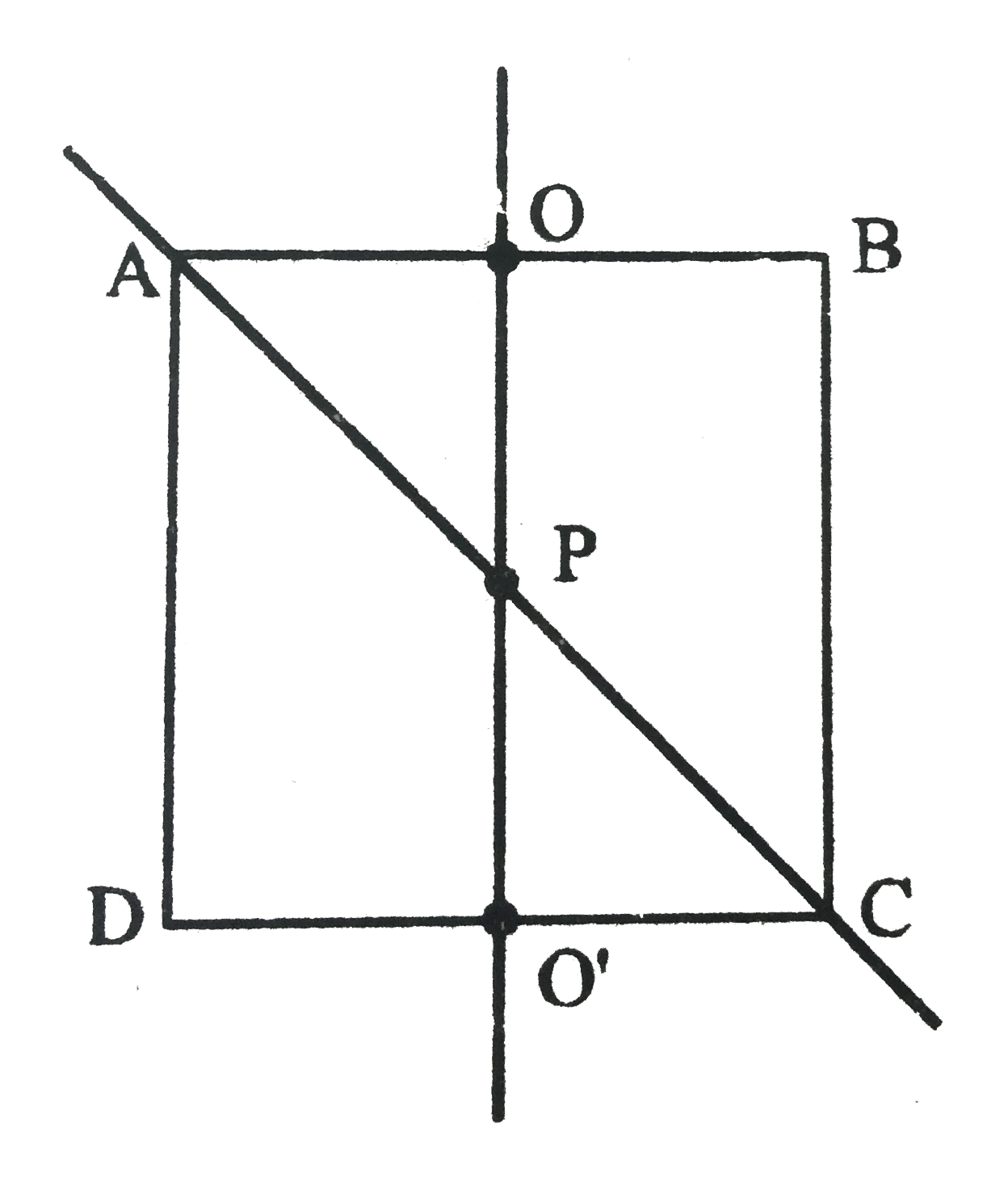 .
.
View Solution
Knowledge Check
Let I1andI2 be the moments of inertia of two bodies of identical geometrical shapek, the first made of aluminium and the second of iron.
AI1<IBBI1=I2CI1>I2Drelation between I_1 and I_2 depends on the actual shapes of the bodiesThe moment of inertia of a ring about its geometrical axis is I, then its moment of inertia about its diameter will be
A1 IBI/2CIDI/4
Let I1 and I2 be the moment of inertia of a uniform square plate about axes shown in the figure. Then the ratio I1:I2 isA1:17B1:127C1:712D1:7
Let IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not
View SolutionLet IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not
View SolutionI1,I2 are moments of inertia of two solid spheres of same mass about axes passing through their centres. If first is made of wood and the second is made of steel, then
View SolutionStatement-1 : Moment of inertia of a body is same, whatever be the axis of rotation.
Statement-2 : Moment of inertia depends on mass and size of rotation of the body.
View SolutionThe moments of inertia of two rotating bodies A and are IA and IB(IA>IB). If their angular momenta are equal then.
View Solution
