A metre long narrow bore held horizontally (and closed at one end) contains a 76 cm long mercury thread, which traps a 15 cm column of air. What happens if the tube is held vertically with the open end at the bottom ?

Video Solution

Text Solution

Verified by Experts

If a is the area of cross- section of the tube (a),

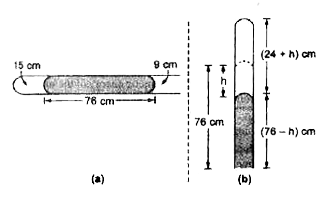
Inilial volume of air, $V_{1} = 15$ a
initial pressure of air,
$p_{1}$ 76 cm (of He column)
On holding this tube of narrow bore vertically (b), let h be the vertical distance through which the mercury in the tube gets depressed to balance the atmospheric pressure. Obviously, h denotes the final pressure of air, i.e., $P_{2} = h$ .
It is to be noted that the length of the air column left
= length of the tube - length of Hg column
$100 - (76 - h) = (24 + h)$
Final volume , $V_{2} = (24 + h) a$
Applying Boyle.s law,
$P_{1} V_{1} = P_{2} V_{2} or 76 \times 15 a$ = h (24 + h)a
or $1140 = 24 h + h^{2} or h^{2} + 24 h - 1140 = 0$
or $h = \frac{- 24 + \sqrt{{(24)}^{2} + 4 \times 1 \times 1140}}{2}$
since h cannot be negative tube, h = 23.8 cm .
Thus, in the vertical position of lhe tube, 23.8 cm of rnercury flows out and the remaining 52.2 cm of n1ercury thread plus the 48 cm of air above it remain in equilibriun with the outside atmospheric pressure.

Updated on:21/07/2023

A thin tube of uniform cross-section is sealed at both ends. It lies horizontally, the middle 5 cm containing mercury and the two equal end containing air at the same pressure P. When the tube is held at an angle of $60^{\circ}$ with the vetical direction, the length of the air column above and below the mercury column are 46 cm and 44.5 cm respectively. Calculate the pressure P in centimeters of mercury. (The temperature of the system is kept at $30^{\circ} C$ ).
A $75.4$
B $45.8$
C $67.5$
D $89.3$