A narrow tube 50 cm length is closed at one end contains air trapped by a certain column of Hg. When the tubes is held horizontally, the air column in if has a length of 10cm. What is the pressure exerted by air when the tube is held vertically with the open end at the bottom and the length of the air column is 15cm? Also find the vertical height of the mercury column inside the tube.
To solve the problem step by step, we will use Boyle's Law, which states that the pressure of a gas multiplied by its volume is a constant when the temperature is constant.
Step 1: Understand the Initial Conditions
- The tube is closed at one end and contains air trapped by a column of mercury (Hg).
- When held horizontally, the length of the air column (L1) is 10 cm.
- The pressure of the air column (P1) when the tube is horizontal is equal to the atmospheric pressure, which is 76 cm of Hg.
Step 2: Calculate the Pressure When the Tube is Vertical
- When the tube is held vertically, the length of the air column (L2) is 15 cm.
- According to Boyle's Law, we have the relationship:
P1⋅L1=P2⋅L2
where P2 is the pressure of the air when the tube is vertical.
Step 3: Substitute the Known Values
- Substitute P1 = 76 cm Hg, L1 = 10 cm, and L2 = 15 cm into the equation:
76⋅10=P2⋅15
Step 4: Solve for P2
- Rearranging the equation gives:
P2=76⋅1015
- Calculate P2:
P2=76015≈50.67 cm Hg
Step 5: Calculate the Height of the Mercury Column (H)
- The pressure exerted by the air (P2) plus the pressure due to the height of the mercury column (H) must equal atmospheric pressure:
P2+H=76 cm Hg
- Rearranging gives:
H=76−P2
- Substitute P2:
H=76−50.67≈25.33 cm Hg
Final Answers
- The pressure exerted by the air when the tube is vertical is approximately 50.67 cm Hg.
- The vertical height of the mercury column inside the tube is approximately 25.33 cm Hg.
- The tube is closed at one end and contains air trapped by a column of mercury (Hg).
- When held horizontally, the length of the air column (L1) is 10 cm.
- The pressure of the air column (P1) when the tube is horizontal is equal to the atmospheric pressure, which is 76 cm of Hg.
- When the tube is held vertically, the length of the air column (L2) is 15 cm.
- According to Boyle's Law, we have the relationship:
P1⋅L1=P2⋅L2
where P2 is the pressure of the air when the tube is vertical.
- Substitute P1 = 76 cm Hg, L1 = 10 cm, and L2 = 15 cm into the equation:
76⋅10=P2⋅15
- Rearranging the equation gives:
P2=76⋅1015
- Calculate P2:
P2=76015≈50.67 cm Hg
- The pressure exerted by the air (P2) plus the pressure due to the height of the mercury column (H) must equal atmospheric pressure:
P2+H=76 cm Hg
- Rearranging gives:
H=76−P2
- Substitute P2:
H=76−50.67≈25.33 cm Hg
- The pressure exerted by the air when the tube is vertical is approximately 50.67 cm Hg.
- The vertical height of the mercury column inside the tube is approximately 25.33 cm Hg.
Topper's Solved these Questions
- PROPERTIES OF MATTERBook:ICSEChapter:PROPERTIES OF MATTERExercise:MODULE 4 (SOLVED EXAMPLES)
Explore 11 Videos
- PROPERTIES OF MATTERBook:ICSEChapter:PROPERTIES OF MATTERExercise:MODULE 1 (ELASTICITY)
Explore 2 Videos
- PROPERTIES OF MATTERBook:ICSEChapter:PROPERTIES OF MATTERExercise:MODULE 2 (SOLVED EXAMPLES)
Explore 22 Videos
- OSCILLATIONS Book:ICSEChapter:OSCILLATIONS Exercise:SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
Explore 2 Videos
- SAMPLE QUESTION PAPER - 01 Book:ICSEChapter:SAMPLE QUESTION PAPER - 01 Exercise:SECTION - D
Explore 12 Videos
Similar Questions
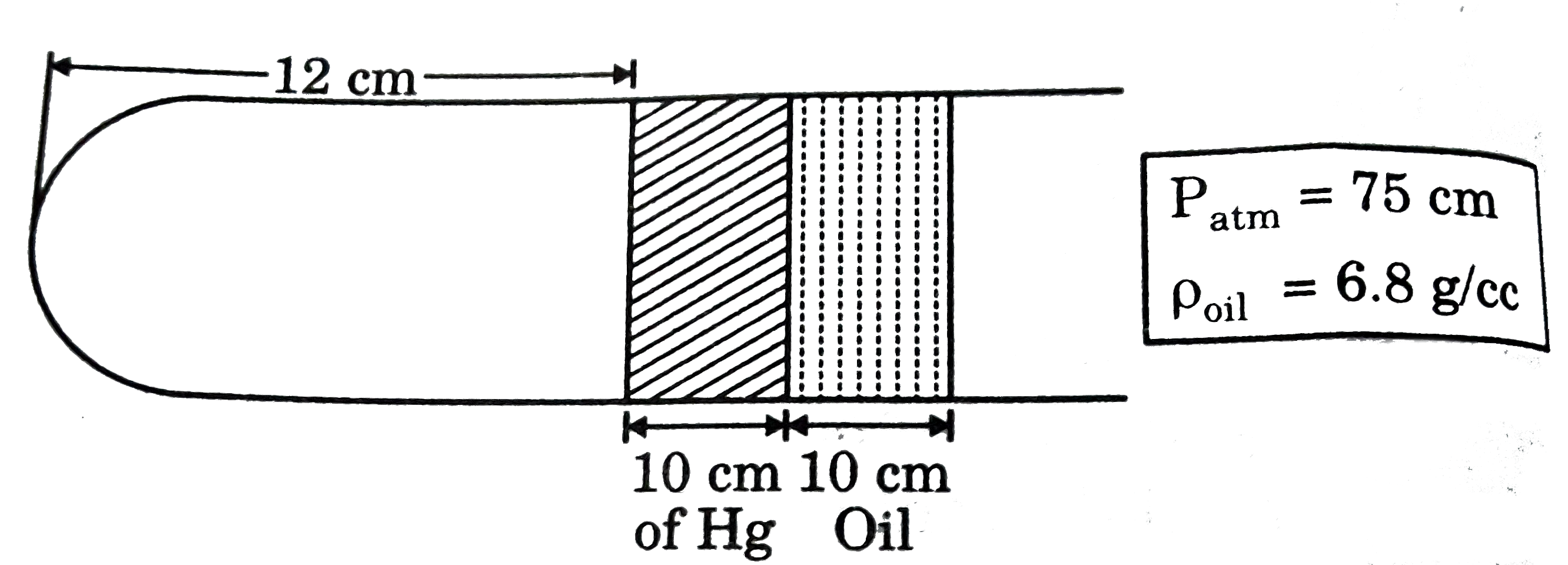
If above tube is placed vertically with the open and upward then find the length of the air column.
View SolutionA 10.0 cm column of air is trapped by a column of Hg 4.00 cm long in capillary tube of uniform bore when the tube is held horizontally in a room at 1 atm. Length of the air column when the tube is held vertically with the open end up is

View SolutionA metre long narrow bore held horizontally (and close at one end) contains a 76 cm long mercury thread, which traps a 15 cm column of air. What happens if the tube is held vertically with the open end at the bottom?
View SolutionA uniform tube closed at one end, contains a pallet of mercury 4 cm long. When the tube is kept vertically with closed end upwards, the length of air column between closed end and mercury pallet is 10 cm. the tube is inverted so that open end becomes upwards. find the length of trapped air column (in cm) trapped. take atmospheric pressure 76 cm of Hg.
View SolutionAir is trapped in a horizontal glass tube by 36 cm mercury column as shown below :
 If the tube is held vertical keeping the open end up, lengh of air column shrink to 19 cm. What is the lengh (in cm) by which the mercury column shifts down?
If the tube is held vertical keeping the open end up, lengh of air column shrink to 19 cm. What is the lengh (in cm) by which the mercury column shifts down?
View SolutionIn given figure, A uniform cylindrical tube closed at one end, contains a pallet of mercury 5cm long. When the tube is kept verticaly with the closed end downward, the length of the air column trapped is 30cm. Now the tube is inverted so that the closed end goes up find the new length of the air column trapped. atmospheric pressure =75cm of mercury. (Assume temperature remains constant in this process)

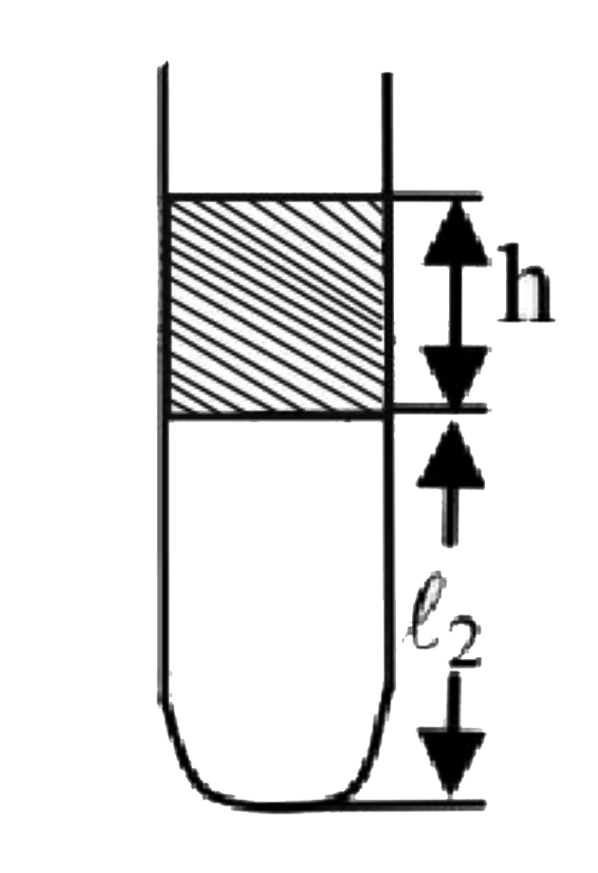
View SolutionAn air column closed in a tube sealed at one end by a Hg column having height h. When the tube is placed with open end down, the height of the air column Iis l1. If the tube is turned so that its open end is at the top, the height of the air column is l2. What is the atmospheric pressure (P0).
View SolutionThe frequency of sound increases when the closed length of an air column :
View SolutionA narrow pipe of length 2m is closed at one end. The velocity of sound in air is 320 m/s. Neglecting end corrections , the air column in the pipe will resonate for sound of frequencies :
View SolutionA uniform tube closed at aone end, contains a pellet of mercury 10cm long. When the tube is lept vertically with the closed-end upward, the length of the air column trapped is 20cm. Find the length of the air column trapped when the tube is inverted so that the closed-end goes down. Atmospheric pressure=75cm of mercury.
View Solution

