A metre long narrow bore held horizontally (and close at one end) contains a 76 cm long mercury thread, which traps a 15 cm column of air. What happens if the tube is held vertically with the open end at the bottom?
To solve the problem step by step, we will analyze the situation when the tube is held vertically with the open end at the bottom.
Step 1: Understand the Initial Setup
- The tube is 1 meter long and closed at one end.
- It contains a 76 cm long mercury thread and traps a 15 cm column of air.
- The remaining length of the tube (1 m - 76 cm - 15 cm) is 9 cm, which is empty.
Step 2: Analyze the Situation When the Tube is Held Vertically
- When the tube is held vertically with the open end at the bottom, the mercury will be affected by atmospheric pressure acting on it from below.
- The atmospheric pressure (P_atm) will push up on the mercury column.
Step 3: Define Initial and Final Pressures
- The initial pressure (P1) acting on the trapped air column when the tube is horizontal is the pressure due to the mercury column plus atmospheric pressure:
P1=Patm+(76 cm Hg)
- The final pressure (P2) when the tube is vertical will be the atmospheric pressure minus the height of the mercury column (H):
P2=Patm−H
Step 4: Use the Ideal Gas Law
- Since the process is isothermal (constant temperature), we can use the ideal gas law:
P1V1=P2V2
- Here, V1 is the initial volume of the air column (15 cm), and V2 is the final volume when the air expands.
Step 5: Calculate Initial and Final Volumes
- The initial volume V1 of the air column is:
V1=A⋅15 cm
- The final volume V2 when the air expands will be:
V2=A⋅(24+H) cm
(where 24 cm is the length of the air column plus the 9 cm of empty space).
Step 6: Set Up the Equation
- Substituting P1 and P2 into the ideal gas equation:
(Patm+76)⋅(A⋅15)=(Patm−H)⋅(A⋅(24+H))
- Cancel out the area A from both sides:
(Patm+76)⋅15=(Patm−H)⋅(24+H)
Step 7: Solve for H
- Rearranging gives us a quadratic equation in terms of H:
76⋅15=H⋅(24+H)+Patm⋅24
- Solve this quadratic equation using the quadratic formula:
H=−b±√b2−4ac2a
- Substitute the values to find H.
Step 8: Calculate the Result
- After solving the quadratic equation, we find the positive root for H, which is approximately 23.84 cm.
- The final volume of the air column is:
V2=A⋅(24+23.84)=A⋅47.84 cm
Conclusion
When the tube is held vertically with the open end at the bottom, the air column expands, and the new height of the air column becomes approximately 47.84 cm.
---
- The tube is 1 meter long and closed at one end.
- It contains a 76 cm long mercury thread and traps a 15 cm column of air.
- The remaining length of the tube (1 m - 76 cm - 15 cm) is 9 cm, which is empty.
- When the tube is held vertically with the open end at the bottom, the mercury will be affected by atmospheric pressure acting on it from below.
- The atmospheric pressure (P_atm) will push up on the mercury column.
- The initial pressure (P1) acting on the trapped air column when the tube is horizontal is the pressure due to the mercury column plus atmospheric pressure:
P1=Patm+(76 cm Hg)
- The final pressure (P2) when the tube is vertical will be the atmospheric pressure minus the height of the mercury column (H):
P2=Patm−H
- Since the process is isothermal (constant temperature), we can use the ideal gas law:
P1V1=P2V2
- Here, V1 is the initial volume of the air column (15 cm), and V2 is the final volume when the air expands.
- The initial volume V1 of the air column is:
V1=A⋅15 cm
- The final volume V2 when the air expands will be:
V2=A⋅(24+H) cm
(where 24 cm is the length of the air column plus the 9 cm of empty space).
- Substituting P1 and P2 into the ideal gas equation:
(Patm+76)⋅(A⋅15)=(Patm−H)⋅(A⋅(24+H))
- Cancel out the area A from both sides:
(Patm+76)⋅15=(Patm−H)⋅(24+H)
- Rearranging gives us a quadratic equation in terms of H:
76⋅15=H⋅(24+H)+Patm⋅24
- Solve this quadratic equation using the quadratic formula:
H=−b±√b2−4ac2a
- Substitute the values to find H.
- After solving the quadratic equation, we find the positive root for H, which is approximately 23.84 cm.
- The final volume of the air column is:
V2=A⋅(24+23.84)=A⋅47.84 cm
When the tube is held vertically with the open end at the bottom, the air column expands, and the new height of the air column becomes approximately 47.84 cm.
Topper's Solved these Questions
- TRANSIENT CURRENTBook:SL ARORAChapter:TRANSIENT CURRENTExercise:Type A
Explore 22 Videos
- TRANSIENT CURRENTBook:SL ARORAChapter:TRANSIENT CURRENTExercise:Type B
Explore 12 Videos
- TRANSIENT CURRENTBook:SL ARORAChapter:TRANSIENT CURRENTExercise:Problems For Self Practice
Explore 17 Videos
- THERMOELECTRICITYBook:SL ARORAChapter:THERMOELECTRICITYExercise:Problems for Self Practice
Explore 13 Videos
- UNIVERSEBook:SL ARORAChapter:UNIVERSEExercise:PROBLEM_TYPE
Explore 6 Videos
Similar Questions
A metre long narrow bore held horizontally (and close at one end) contains a 76 cm long mercury thread, which traps a 15 cm column of air. What happens if the tube is held vertically with the open end at the bottom?
View SolutionIn given figure, A uniform cylindrical tube closed at one end, contains a pallet of mercury 5cm long. When the tube is kept verticaly with the closed end downward, the length of the air column trapped is 30cm. Now the tube is inverted so that the closed end goes up find the new length of the air column trapped. atmospheric pressure =75cm of mercury. (Assume temperature remains constant in this process)

View Solution
Knowledge Check
Some mercury is poured into a capillary tube of uniform bore and one end closed. When the tube is held horizontally, mercury column has a length of 4 cm and air enclosed in the closed end has a length of 10 cm. If the tube is now held vertically, with open end upwards, the length of the air column will be (take atmospheric pressure at the place of experiment to be 760 mm)
A10.5 cmB8.5 cmC9.0 cmD9.5 cmA 10.0 cm column of air is trapped by a column of Hg 4.00 cm long in capillary tube of uniform bore when the tube is held horizontally in a room at 1 atm. Length of the air column when the tube is held vertically with the open end up is
 A9.50 cmB10.52 cmC3.53 cmD4.61 cm
A9.50 cmB10.52 cmC3.53 cmD4.61 cmA mercury tube of length
100 cm. open at one end is kept
vertically with open end upwards. It
is filled with 10 cm of mercury to
trap an air column of height
40 cm. what will be the length of
trapped air if it is held vertically
with open end downwards ?
[ Assume atmospheric pressure to be 1 atm]A40.00 cmB32.00 cmC52.12 cmD82.00 cm
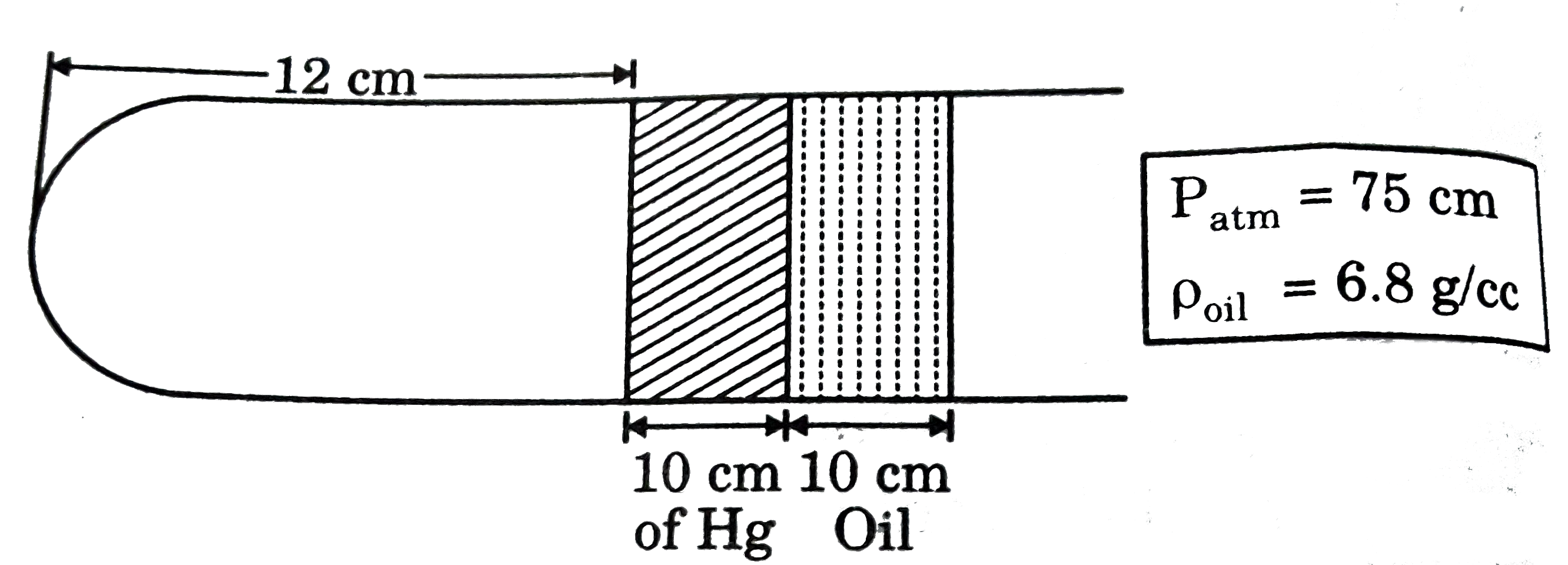
If above tube is held vertical with open end upward then find the length of air column (in cm).
View SolutionA long horizontal glass capillary tube open at both ends contains a mercury thread 1 m long at 0∘C. Find the length of the mercury thread, as read on this scale, at 100∘C.
View SolutionA 10 cm long column of Hg is kept in the middel of a narrow 1 m long tube (both eads closed). The two halves of the tube contains air at a pressure of 76 cm of Hg. Calculate the distance (in cm) when the column of Hg be displaced if the tube is held vertical? Answer should be the closest integer.
View SolutionA thin tube of uniform cross section is sealed at both ends. It lies horizontally, the middle 5cm containing mercury and the parts on its two sides containing air at the same pressure p. When the tube is held at and angle of 60∘ with the vertical, the length of the air column above and below the mercury pellet are 46cm and 44.5cm respectively. Calculate the pressure in centimeters of mercury, The temperature of the system is kept at 30∘C.
View SolutionA column of mercury of 10cm length is contained in the middle of a narrow horizontal 1m long tube which is closed at both the ends. Both the halves of the tube contain air at a pressure of 76 cm of mercury. By what distance will the column of mercury be displaced if the tube is held vertically?
View Solution

