What is the force on a conductor of length l carrying current 'i' when it is situated in a magnetic field of induction B? When is it maximum?
To find the force on a conductor of length l carrying current i when it is situated in a magnetic field of induction B, we can follow these steps:
Step 1: Understand the Force on a Current-Carrying Conductor
The force F acting on a straight conductor carrying a current in a magnetic field can be expressed using the formula:
F=iL×B
where:
- F is the force vector,
- i is the current flowing through the conductor,
- L is the length vector of the conductor in the direction of the current,
- B is the magnetic field vector.
Step 2: Calculate the Magnitude of the Force
To find the magnitude of the force, we can use the following expression:
F=iLBsinθ
where:
- F is the magnitude of the force,
- L is the length of the conductor,
- B is the magnetic field induction,
- θ is the angle between the length vector L and the magnetic field vector B.
Step 3: Determine When the Force is Maximum
The force will be maximum when sinθ is at its maximum value. The maximum value of sinθ is 1, which occurs when:
θ=90∘
This means that the conductor should be perpendicular to the magnetic field for the force to be maximized.
Step 4: Write the Maximum Force Expression
When θ=90∘:
Fmax=iLB
This is the maximum force acting on the conductor.
Summary
- The force on a conductor of length l carrying current i in a magnetic field B is given by F=iLBsinθ.
- The force is maximum when the angle θ between the conductor and the magnetic field is 90∘.
The force F acting on a straight conductor carrying a current in a magnetic field can be expressed using the formula:
F=iL×B
where:
- F is the force vector,
- i is the current flowing through the conductor,
- L is the length vector of the conductor in the direction of the current,
- B is the magnetic field vector.
To find the magnitude of the force, we can use the following expression:
F=iLBsinθ
where:
- F is the magnitude of the force,
- L is the length of the conductor,
- B is the magnetic field induction,
- θ is the angle between the length vector L and the magnetic field vector B.
The force will be maximum when sinθ is at its maximum value. The maximum value of sinθ is 1, which occurs when:
θ=90∘
This means that the conductor should be perpendicular to the magnetic field for the force to be maximized.
When θ=90∘:
Fmax=iLB
This is the maximum force acting on the conductor.
- The force on a conductor of length l carrying current i in a magnetic field B is given by F=iLBsinθ.
- The force is maximum when the angle θ between the conductor and the magnetic field is 90∘.
Topper's Solved these Questions
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - PROBLEMS (LEVEL -I)
40 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - PROBLEMS (LEVEL -II)
40 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS)
6 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
5 Videos
Similar Questions
A conductor (rod) of mass m, length l carrying a current i is subjected to a magnetic field of induction B. If the coefficients of friction between the conducting rod and rail is μ, find the value of I if the rod starts sliding.
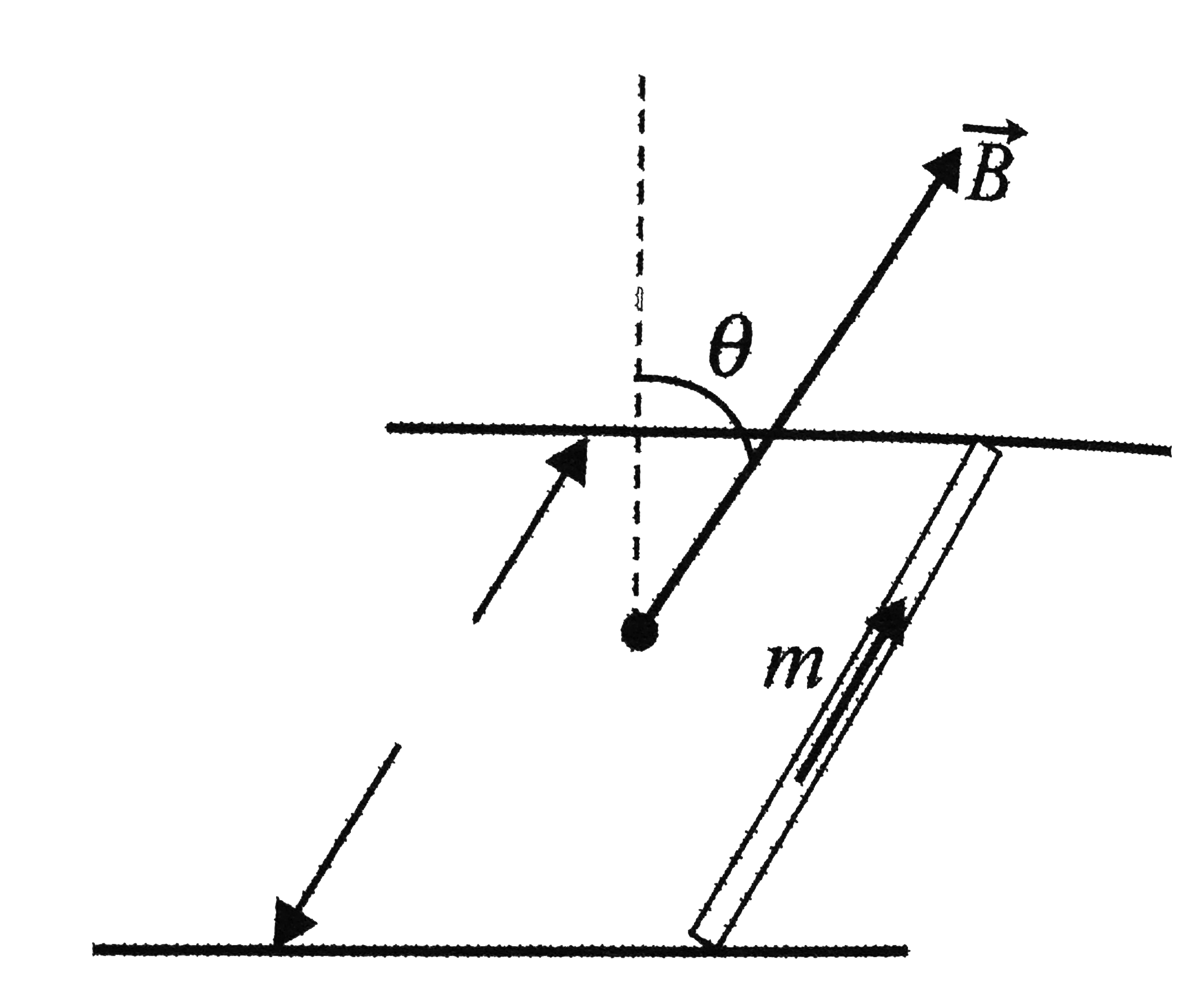
View SolutionA long current carrying wire is bent as shown. The magnetic field induction at O is

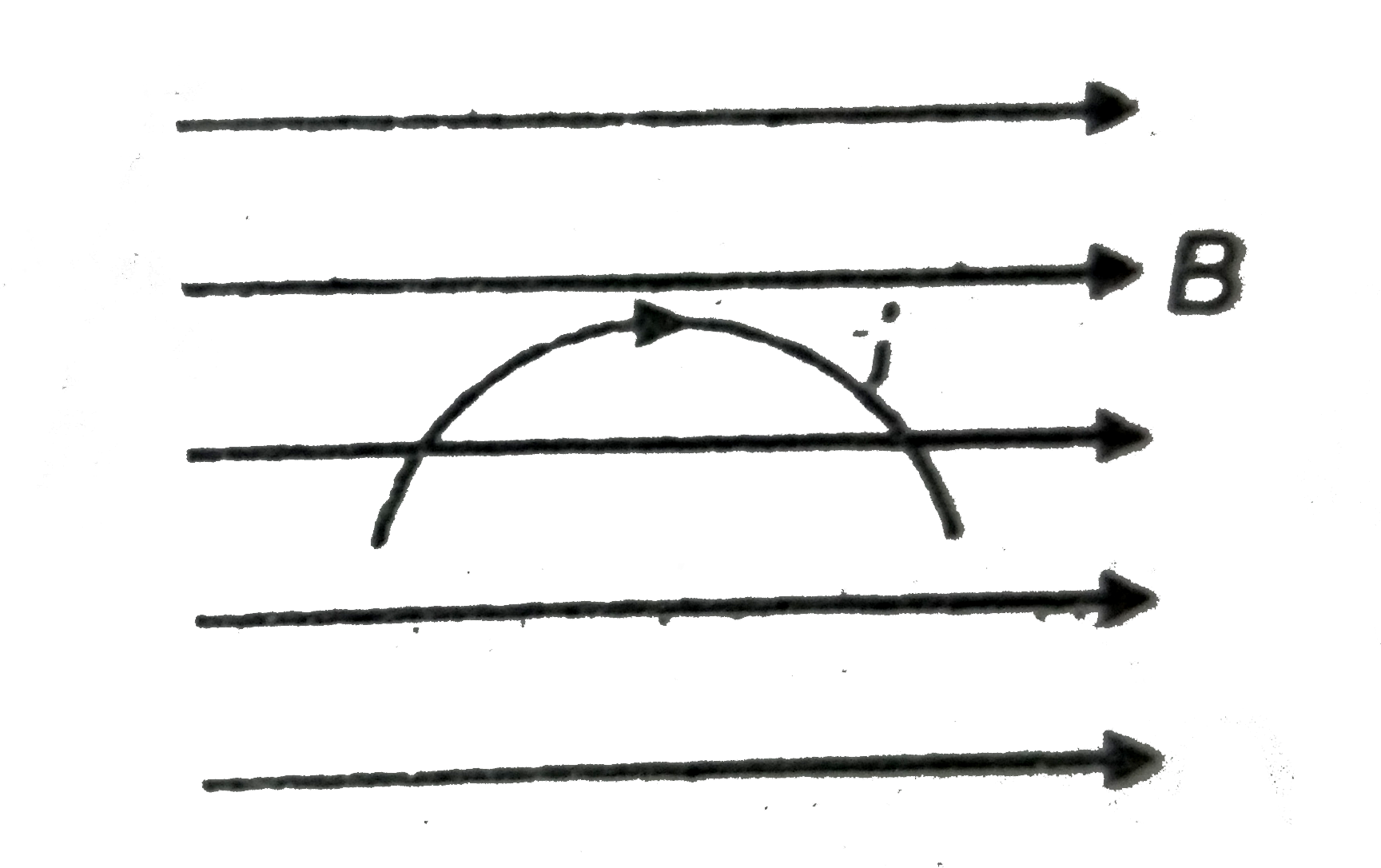
View SolutionWhat is the force experienced by a semicircular wire of radius R when it is carrying a current l and is placed in a uniform magnetic field of induction B as shown in figure. ?
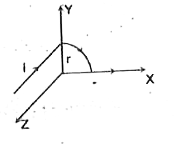
View SolutionShown in the figure is a conductor carrying a current i. the magnetic field at the origin is :
View SolutionA conductor of length L and carrying current i is bent to form a coil of two turns.Magnetic field at the centre of the coil will be
View SolutionMagnetic lines of force due to a straight conductor carrying current are
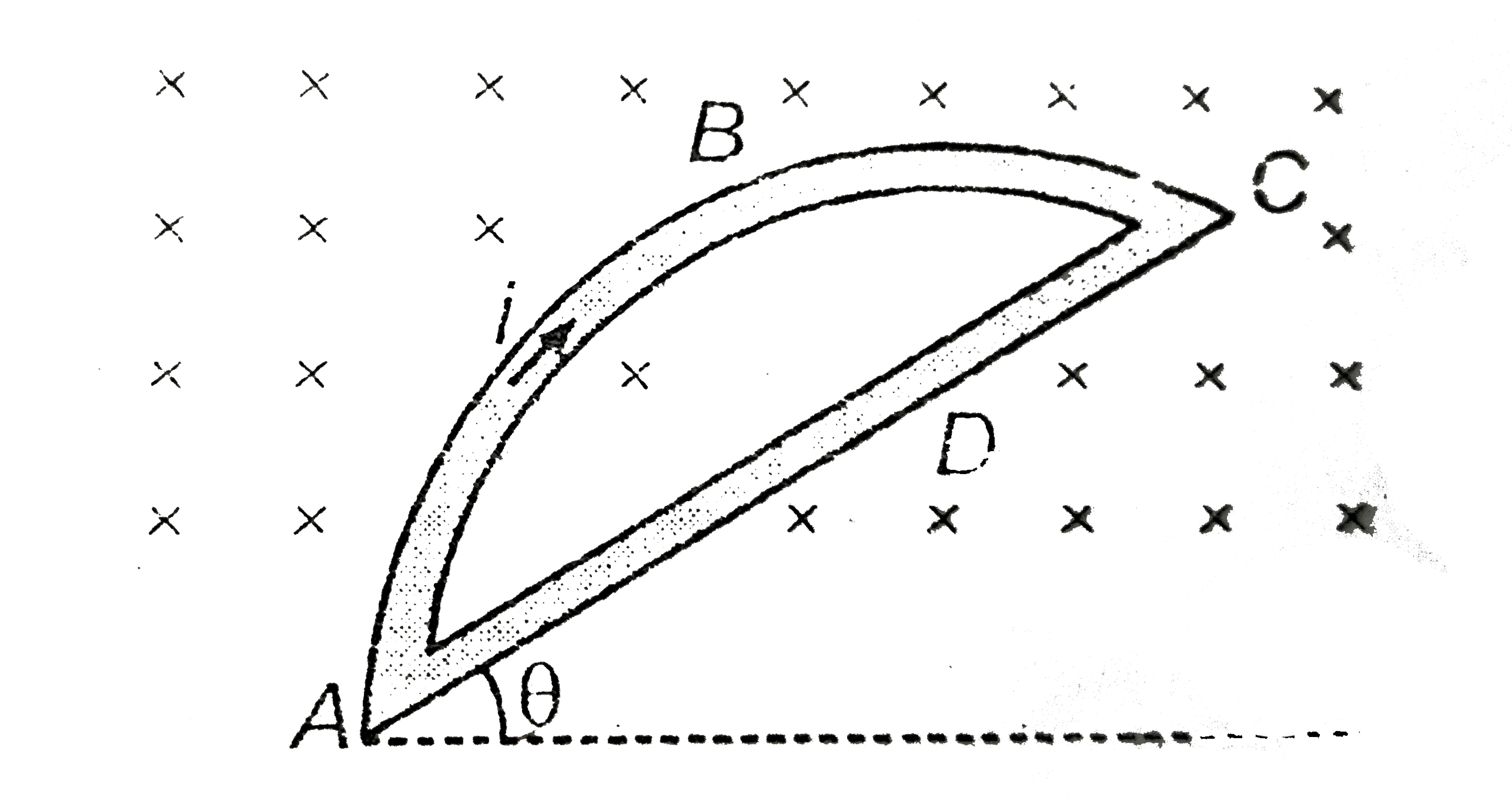
View SolutionA circular wire ABC and a straight conductor ADC are carrying current i and are kept in the magnetic field B then
View SolutionA straight wire of length 0.5 metre and carrying a current of 1.2 ampere is placed in a uniform magnetic field of induction 2 tesla. If the magnetic field is perpendicular to the length of the wire , the force acting on the wire is
View SolutionFigure shows a straight wire of length a carrying a current I. What is the magnitude of magnetic field induction produced by the current at P, which is lying at a perpendicular distance a from one end of the wire.


View SolutionShown in Fig. is a conductor carrying current I. Find the magnetic field intensity at point O.
View Solution
