What is the work done in taking a north pole of strength m around a long and straight conductor in a circular path at a perpendicular distance of r from the straight conductor?
To solve the problem of calculating the work done in taking a north pole of strength m around a long and straight conductor in a circular path at a perpendicular distance r from the conductor, we can follow these steps:
1. Understand the Concept of Work Done:
Work done W is defined as the product of the force F acting on an object and the displacement d of that object in the direction of the force. Mathematically, it can be expressed as:
W=F⋅d=F⋅d⋅cos(θ)
where θ is the angle between the force and displacement vectors.
2. Identify the Force Acting on the Magnetic Pole:
The force F acting on the north pole of strength m in a magnetic field B is given by:
F=m⋅B
We need to determine the magnetic field B at a distance r from the long straight conductor carrying current i.
3. Calculate the Magnetic Field B:
The magnetic field B around a long straight conductor carrying current i at a distance r is given by:
B=μ0i2πr
where μ0 is the permeability of free space.
4. Substitute B into the Force Equation:
Now, substituting the expression for B into the force equation, we get:
F=m⋅(μ0i2πr)=μ0im2πr
5. Determine the Displacement:
When the north pole moves in a circular path around the conductor at a distance r, the displacement d is equal to the circumference of the circle:
d=2πr
6. Calculate the Work Done:
Since the angle θ between the force and displacement is 0∘ (both are in the same direction), we can simplify the work done to:
W=F⋅d=(μ0im2πr)⋅(2πr)
The 2πr terms cancel out:
W=μ0im
Final Answer:
The work done in taking a north pole of strength m around a long and straight conductor in a circular path at a perpendicular distance r from the conductor is:
W=μ0im
Work done W is defined as the product of the force F acting on an object and the displacement d of that object in the direction of the force. Mathematically, it can be expressed as:
W=F⋅d=F⋅d⋅cos(θ)
where θ is the angle between the force and displacement vectors.
The force F acting on the north pole of strength m in a magnetic field B is given by:
F=m⋅B
We need to determine the magnetic field B at a distance r from the long straight conductor carrying current i.
The magnetic field B around a long straight conductor carrying current i at a distance r is given by:
B=μ0i2πr
where μ0 is the permeability of free space.
Now, substituting the expression for B into the force equation, we get:
F=m⋅(μ0i2πr)=μ0im2πr
When the north pole moves in a circular path around the conductor at a distance r, the displacement d is equal to the circumference of the circle:
d=2πr
Since the angle θ between the force and displacement is 0∘ (both are in the same direction), we can simplify the work done to:
W=F⋅d=(μ0im2πr)⋅(2πr)
The 2πr terms cancel out:
W=μ0im
The work done in taking a north pole of strength m around a long and straight conductor in a circular path at a perpendicular distance r from the conductor is:
W=μ0im
Topper's Solved these Questions
- ELECTROMAGNETICSBook:AAKASH SERIESChapter:ELECTROMAGNETICSExercise:PROBLEMS (LEVEL -I)
Explore 40 Videos
- ELECTROMAGNETICSBook:AAKASH SERIESChapter:ELECTROMAGNETICSExercise:PROBLEMS (LEVEL -II)
Explore 40 Videos
- ELECTROMAGNETICSBook:AAKASH SERIESChapter:ELECTROMAGNETICSExercise:EXERCISE (SHORT ANSWER QUESTIONS)
Explore 6 Videos
- ELECTROMAGNETIC WAVESBook:AAKASH SERIESChapter:ELECTROMAGNETIC WAVESExercise:EXERCISE -II
Explore 22 Videos
- ELECTROSTATICSBook:AAKASH SERIESChapter:ELECTROSTATICSExercise:ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
Explore 5 Videos
Similar Questions
How much work is done in taking an electron around a nucleus in a circular path?
View SolutionA magnetic pole of strength 4 Am is moved twice around a long straight wire carrying a current of 3A. The work done is
View SolutionA straight conductor of length 32 cm carries a current of 30A. Magnetic induction at a point which is in air at a perpendicular distance of 12cm from the mid point of the conductor is
View SolutionFind the magnetic induction due to a straight conductor of length 16cm carrying current of 5A at a distance of 6cm from the midpoint of conductor
View SolutionA square loop, carrying a steady current I, is placed in a horizontal plane near a long straight conductor carrying a steady current I1 at a distance d from the donductor as shown in figure. The loop will experience
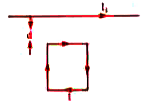
View SolutionA current 'I' flows along an infinitely long straight conductor. If 'r' is the perpendicular distance of a point from the lower end of the conductor, then the magnetic induction B is given by
View SolutionAn electron is ejected from the surface of a long, thick straight conductor carrying a current, initially in a direction perpendicular to the conductor. The electron will
View SolutionA long straight vertical conductor carries a current of 8A in the upward direction. What the magnitude of the resultant magnetic induction at a point in the horizonatal plane at a distance of 4 cm from the conductor towards South? (The horizontal compo-nent of earth's magnetic induction =4×10−5T)
View SolutionWhat is the amount of work done in moving a point charge around a circular are of radius r at the centre where another point charge is located ?
View Solution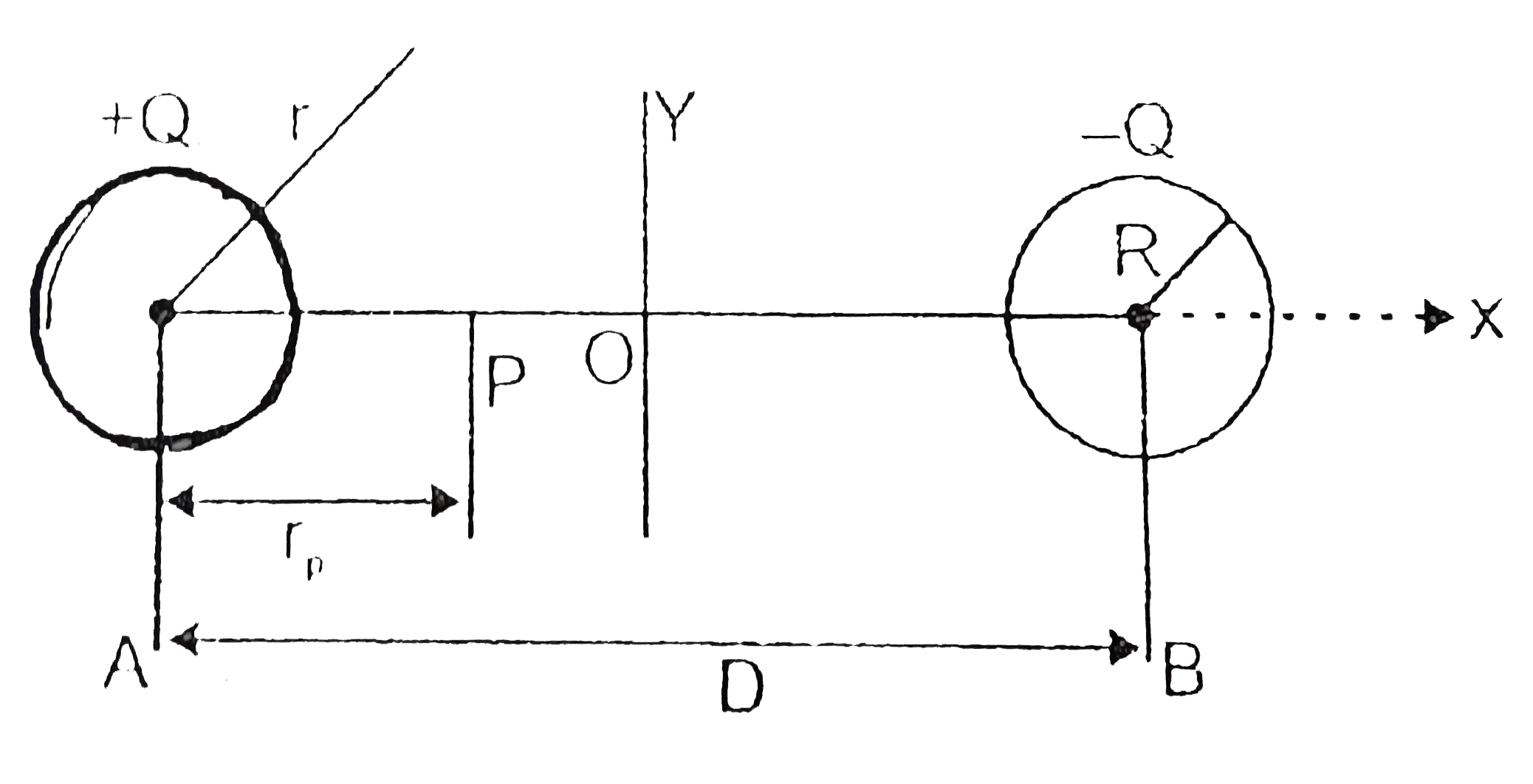
The figure shows two identical long straight metal wires, A and B placed parallel to z-axis the cross sectional radius of each wire is R and the separation of the two wires is D>>R. The electric potential at a perpendicular distance r>R from a long straight wire due to that wire is given by V=−kln(rR) where k is a positive constant. the wires carry charges +Q and −Q per unit length respectively. Then
Q. As D>>R, the electric field due to a long straight wire has cylindrical symmetry. The charge per unit length of the wire is
View Solution