A conductor (rod) of mass m, length l carrying a current i is subjected to a magnetic field of induction B. If the coefficients of friction between the conducting rod and rail is μ, find the value of I if the rod starts sliding.
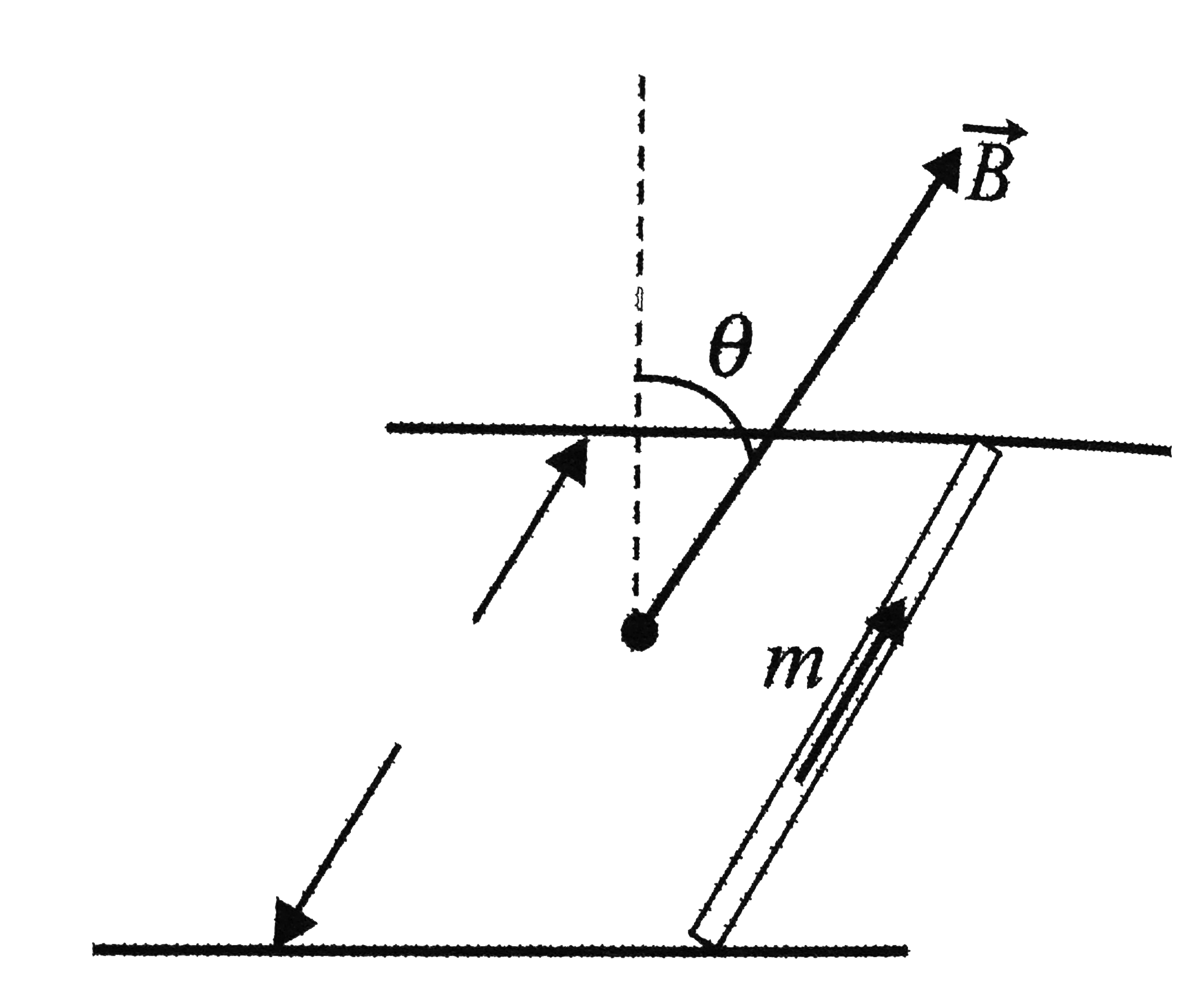
The magnetic force is Fm=ilBsinφ,
where φB =Angle between current and magnetic field =90∘.
or Fm=ilB
but it acts at an angle θ with horizontal as shown in Fig. according to Fleming's left hand rule.
Then the net force along x- and y-axis are
Fy=N−(mg+Fmsinθ)=0
or N=mg+Fmsinθ....(i)
Fx=f−Fmcosθ=0....(ii)
or f=Fmcosθ
Law of friction, f=μN....(iii)
By using the above equations
μ(mg+Fmsinθ)=Fmcosθ
or Fm=μmgcosθ−μsinθorilB=μmgcosθ−μsinθ
or i=μmglB(cosθ−μsinθ)
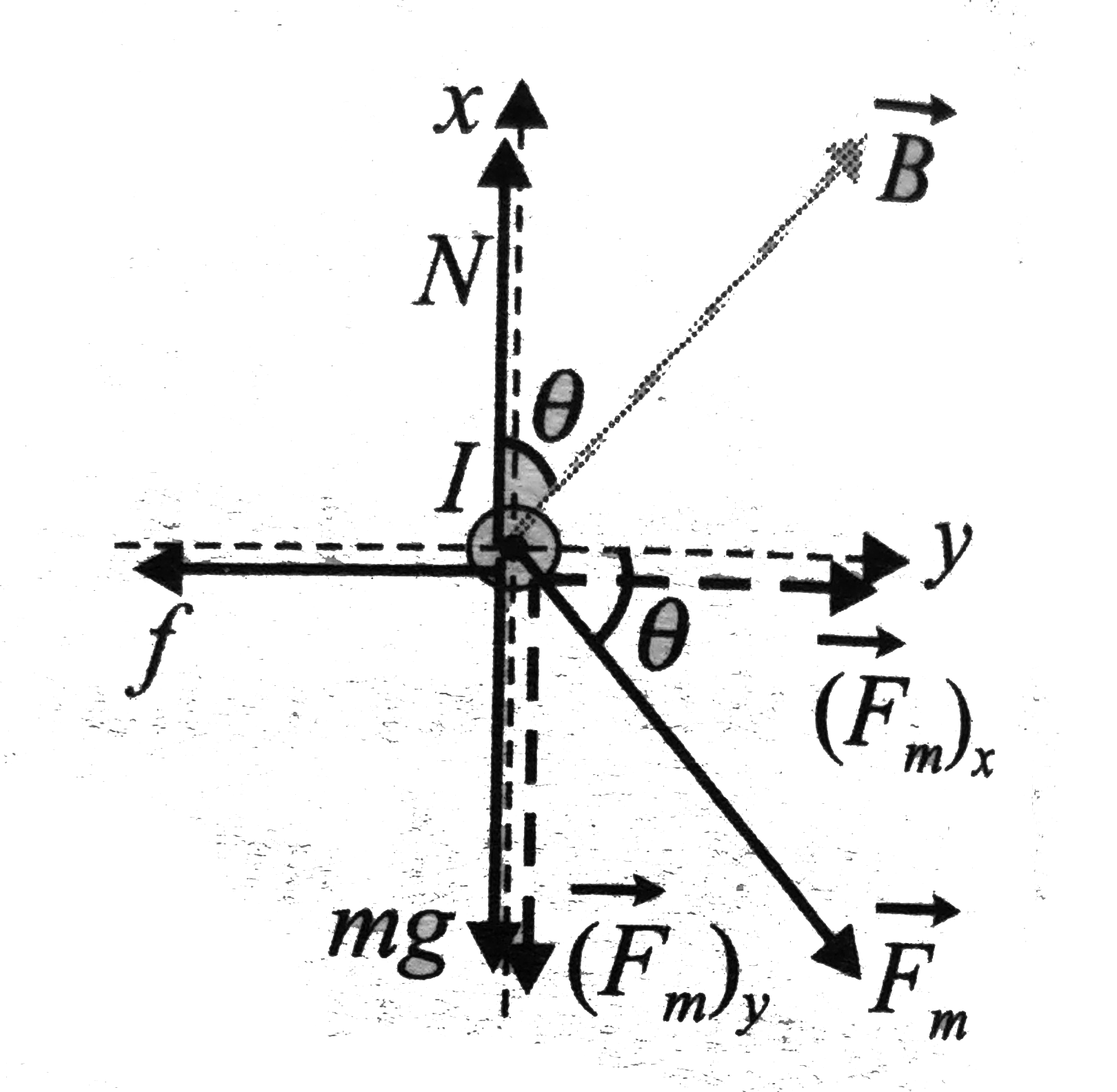 .
.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Solved Example
25 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise 1.1
22 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
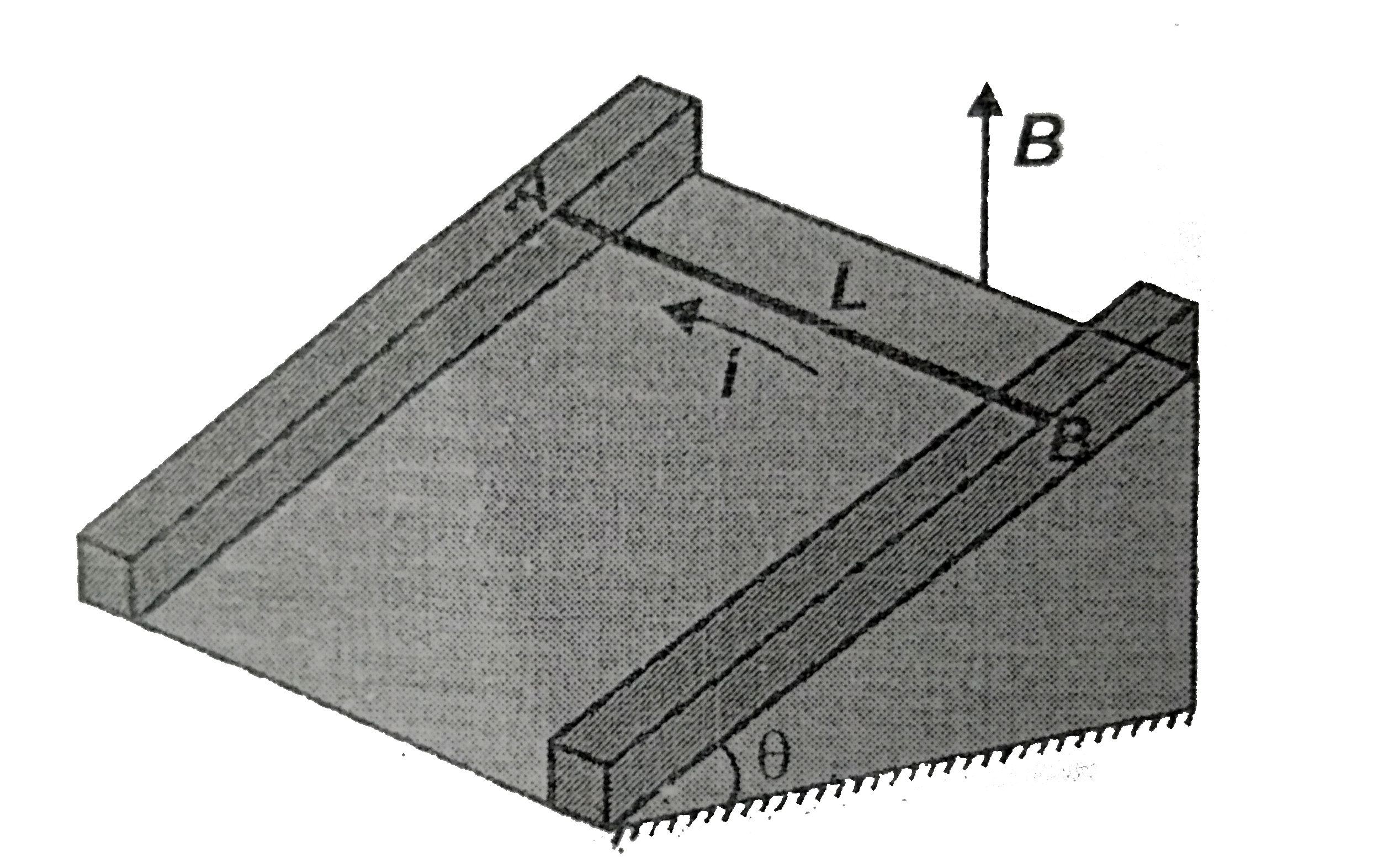
On an inclined plane, two conducting rails are fixed along the line of greatest slope. A conducting rod AB is placed on the radils so that it is horizontal. A vertically upward uniform magnetic field is present in the region. A current i flows through AB from B to A. The mass of AB is m and the coefficient of friction between the rod and rails is μ. Find the minimum and maximum value of B, so that the rod can stay in equilibrium. Assume that μ<tanθ
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is (dependence on L)
View Solution
Knowledge Check
A copper rod of length L rotates with an angular with an angular speed 'ω' in a uniform magnetic field B. find the emf developed between the two ends of the rod. The field in perpendicular to the motion of the rod.
ABωl2B12Bωl2C2Bωl2D14Bωl2
A conducting rod of length 'l'=2√5 meter and mass 'm'=4kg lies on the horizontal table. Coefficient of friction between the rod and the table is 'μ'=(12). If the current in the conductor si 2 ampere, then find the minimum magnitude of magnetic field strength (in Tesla) such that conducting rod just starts to translate along x -axis (take g=10m/sec2) [neglect the radius of rod]

View SolutionA rod CD of length b carrying a current l, is placed in a magnetic field due to a thin log wire AB carrying currrent I as shown in fig. Then find the net force experienced by the wire
View SolutionA copper rod of mass m rests on two horizontal rails distance L apart and carries a current of I from one rail to the other. The coefficient of static friction between rod and rails is μs What are the (a) magnitude and (b) angle (relative to the vertical) of the smallest magnetic field that puts the rod on the verge of sliding?
View SolutionA conducting rod of length l is moving in a transverse magnetic field of strength B with veocity v. The resistance of the rod is R. The current in the rod is
View SolutionA straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is μ. If the wire carries a current I, what minimum magnetic field should exist in the space in order to slide the wire on the rails.
View SolutionA loop is formed by two parallel conductors connected by a solenoid with inductance L=2H and a conducting rod of mass m=80g, which can freely (without fricition) slide over the conductors. The conductors are located in a horizontal plane in a uniform vertical magnetic field with induction B=4T.
The distance between the conductors is equal to l=4cm. At the moment t=0 the rod is imparted an initial velocity v0=2cm/s directed to the right. Find the amplitude (in cm) for the oscillations of conducting rod, if the electric resistance of the loop is negligible.

View SolutionA small conducting rod of length l, moves with a uniform velocity v in a uniform magnetic field B as shown in fig __

View Solution
