Frequency of a particle executing SHM is 10 Hz. The particle is suspended from a vertical spring. At the highest point of its oscillation the spring is unstretched. Maximum speed of the particle is (g=10m/s2
Mean position of the particle is mgk distance below unstretched position of spring. Therefore, amplitude of oscillation is
A=mgkω=√km=2πf=20π
∴mk=1400π2
Therefore, the maximum speed of particle will be:
vmax=Aω=(g400π2)(20π)=12πm/s
Similar Questions
A particle suspended from a vertical spring oscillates 10 times per second. At the highest point of oscillation the spring becomes unstretched. A. Find the maximum speed of the block. B. Find the speed when the spring is stretched by 0.20 cm. Take g=π2ms−2
View SolutionAmplitude of a particle executing SHM is a and its time period is T. Its maximum speed is
View Solution
Knowledge Check
The kinetic energy of a particle, executing S.H.M. is 16 J when it is in its mean position. IF the amplitude of oscillation is 25 cm and the mass of the particle is 5.12 Kg, the time period of its oscillations is
Aπ/5 secB2πsecC20πsecD5π sec
A mass is suspended from a vertica spring which is executing SHM of frequency 5 Hz.
The spring is unstretched at the highest point of oscillation. Maximum speed of the mass is (take, acceleration due to gravity, g=10m/s2 )
View SolutionDisplacement of a particle executing SHM s x=10(cosπt+sinπt). Its maximum speed is
View SolutionThe displacement of a particle executing SHM is given by
y=0.5 sin100t cm . The maximum speed of the particle is
View SolutionAcceleration -displacemnet graph of a particle executing SHM is as shown in given figure. The time period of its oscillations is (in s)
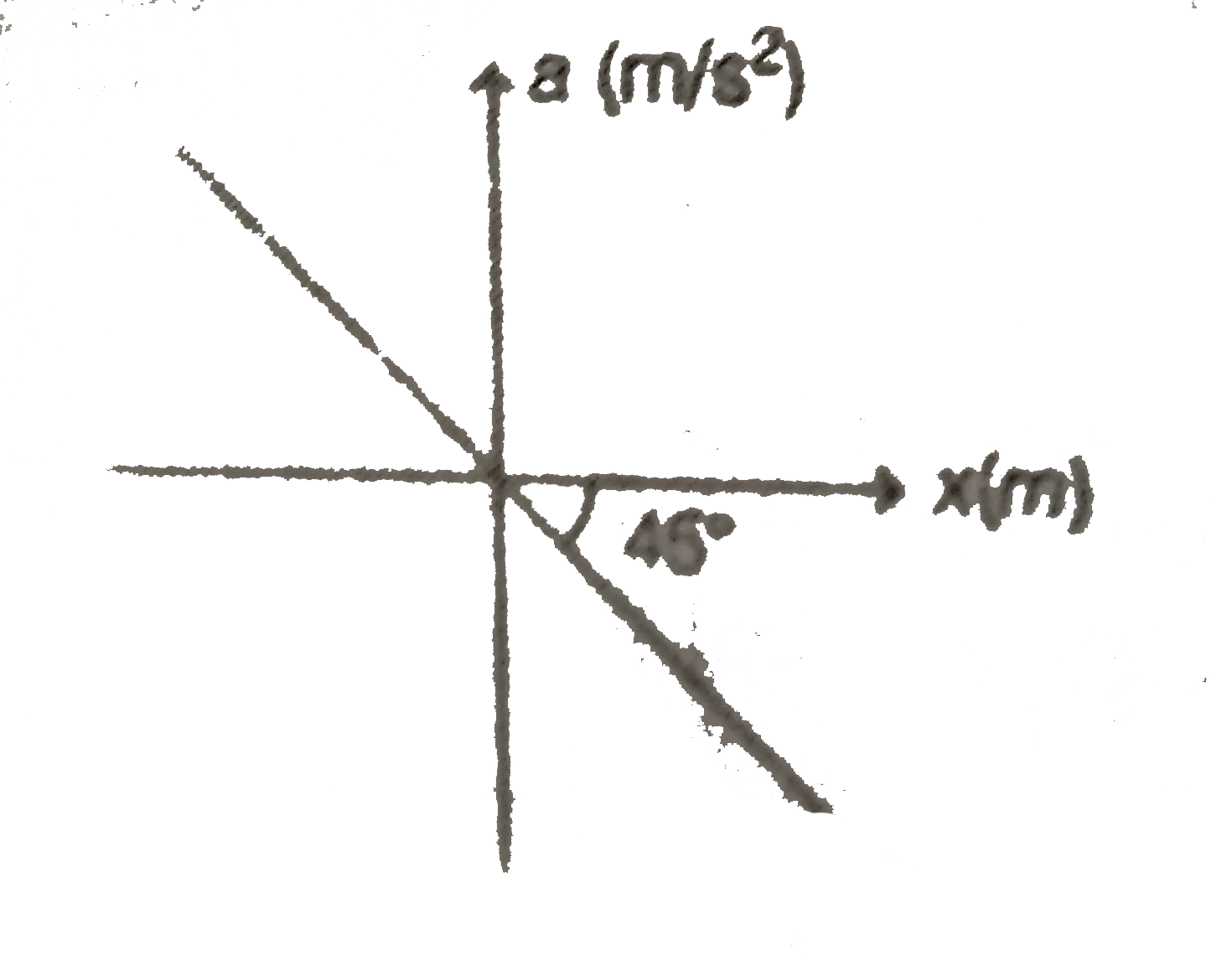
View SolutionThe displacement of a particle executing SHM is given by y=0.25 sin(200t) cm . The maximum speed of the particle is
View SolutionA particle executing SHM has a maximum speed of 30cm/s and a maximum acceleration of 60cms2 . The period of oscillation is
View SolutionA particle executing SHM has a maximum speed of 30cm/s and a maximum acceleration of 60cms2 . The period of oscillation is
View Solution
