Question

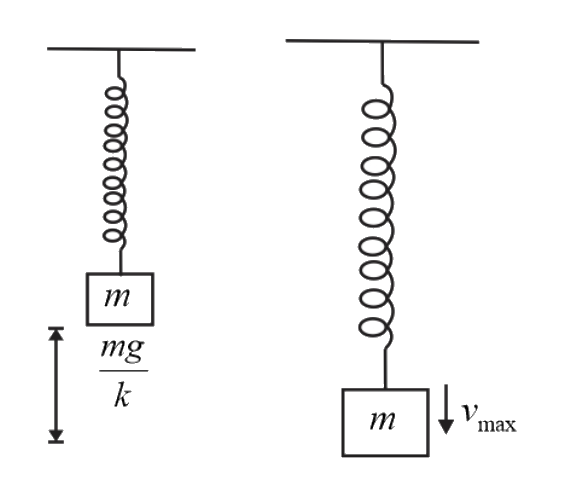
A mass is suspended from a vertica spring which is executing SHM of frequency 5 Hz.
The spring is unstretched at the highest point of oscillation. Maximum speed of the mass is (take, acceleration due to gravity, $g=10m/s^2$ )

Options

A. `2pi m//s`
B. `pi m//s`
C. `(1)/(2pi)m//s`
D. `(1)/(pi)m//s`

Answer

D

Explanation

Given, frequency of SHM (n) =5 Hz
Acceleration due to gravity (g) `=10m//s^(2)`
WE know that,
`T=2pisqrt((m)/(k))`
But frequency, `n=(1)/(T)`
`or" "n=(1)/(2pi)sqrt((k)/(m))or5=(1)/(2pi)sqrt((k)/(m))`
On taking square both sides, we get
`25=(1)/(4pi^(2))(k)/(m)`
`k=100pi^(2)m` . . . (i)
But `kA=mg`
`rArrA=(mg)/(k)` . . . (ii)
Now, `V_(max)=omegaA`
`=(2pi)/(T)xx(mg)/(k)" "` [from Eq. (ii)]
`or" "v_(max)=2pinxx(mg)/(k)" "(becausen=(1)/(T))`
`v_(max)=2pinxx(mg)/(100pi^(2)m)` [from Eq. (i)]
`v_(max)=(nxxg)/(50pi)`
`v_(max)=(5xx10)/(50pi)`
`v_(max)=(1)/(pi)m//s`