A particle of mass m free to move in the x−y plane is subjected to a force whose components are Fx=−kx and Fy=−ky, where k is a constant. The particle is released when t=0 at the point (2,3). Prove that the subsequent motion is simple harmonic along the straight line 2y−3x=0.
Step by step video solution for A particle of mass m free to move in the x - y plane is subjected to a force whose components are F_(x) = - kx and F_(y) = - ky, where k is a constant. The particle is released when t = 0 at the point (2, 3). Prove that the subsequent motion is simple harmonic along the straight line 2y - 3x = 0. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
A particle moving along the x axis is acted upon by a single force F = F0e−kx , where F0 and k are constants. The particle is released from rest at x = 0. It will attain a maximum kinetic energy of :
View SolutionA particle is moving along the y-axis according to the equation[y=a0sin(3ωt)]. The motion is simple harmonic
View SolutionFor a particle moving in the x-y plane, the x and y coordinates are changing as x=a sin ωt and y=a(1−cosωt), where 'a' and ω constants. Then, what can be inferred for the trajectory of the particle ?
View SolutionA particle of mass m initially at rest. A variabl force acts on the particle f=kx2 where k is a constant and x is the displacment. Find the work done by the force f when the speed of particles is v.
View SolutionA particle of mass m initially moving with speed v.A force acts on the particle f=kx where x is the distance travelled by the particle and k is constant. Find the speed of the particle when the work done by the force equals W.
View SolutionA particle moves on the X-axis according to the equation x=x0sin2ωt. The motion simple harmonic
View SolutionA particle moves under the force F(x)=(x2−6x)N, where x is in metres. For small displacements from the origin what is the force constant in the simple harmonic motion approximation ?
View SolutionA particle is moving along the x-axis whose acceleration is given by a=3x−4, where x is the location of the particle. At t = 0, the particle is at rest at x=4/3m. The distance travelled by the particles in 5 s is
View SolutionA particle of mass m=2kg executes SHM in xy- plane between point A and B under action of force →F=Fxˆi+Fyˆj. Minimum time taken by particle to move from A to B is 1 sec. At t=0 the particle is at x=2 and y=2. Then Fx as function of time t is
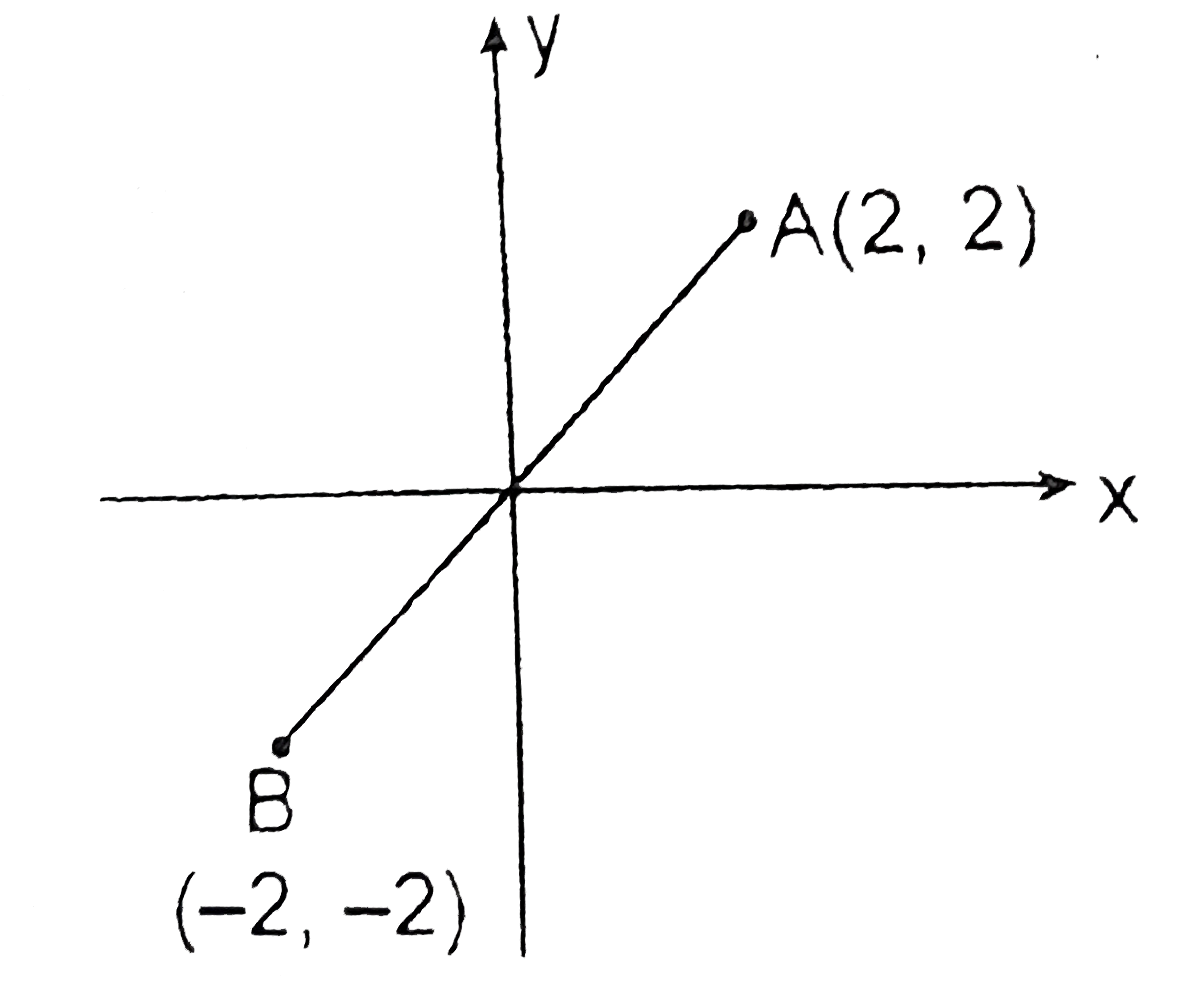
View SolutionA particle of mass m=2kg executes SHM in xy- plane between point A and B under action of force →F=Fxˆi+Fyˆj. Minimum time taken by particle to move from A to B is 1 sec. At t=0 the particle is at x=2 and y=2. Then Fx as function of time t is

View Solution

