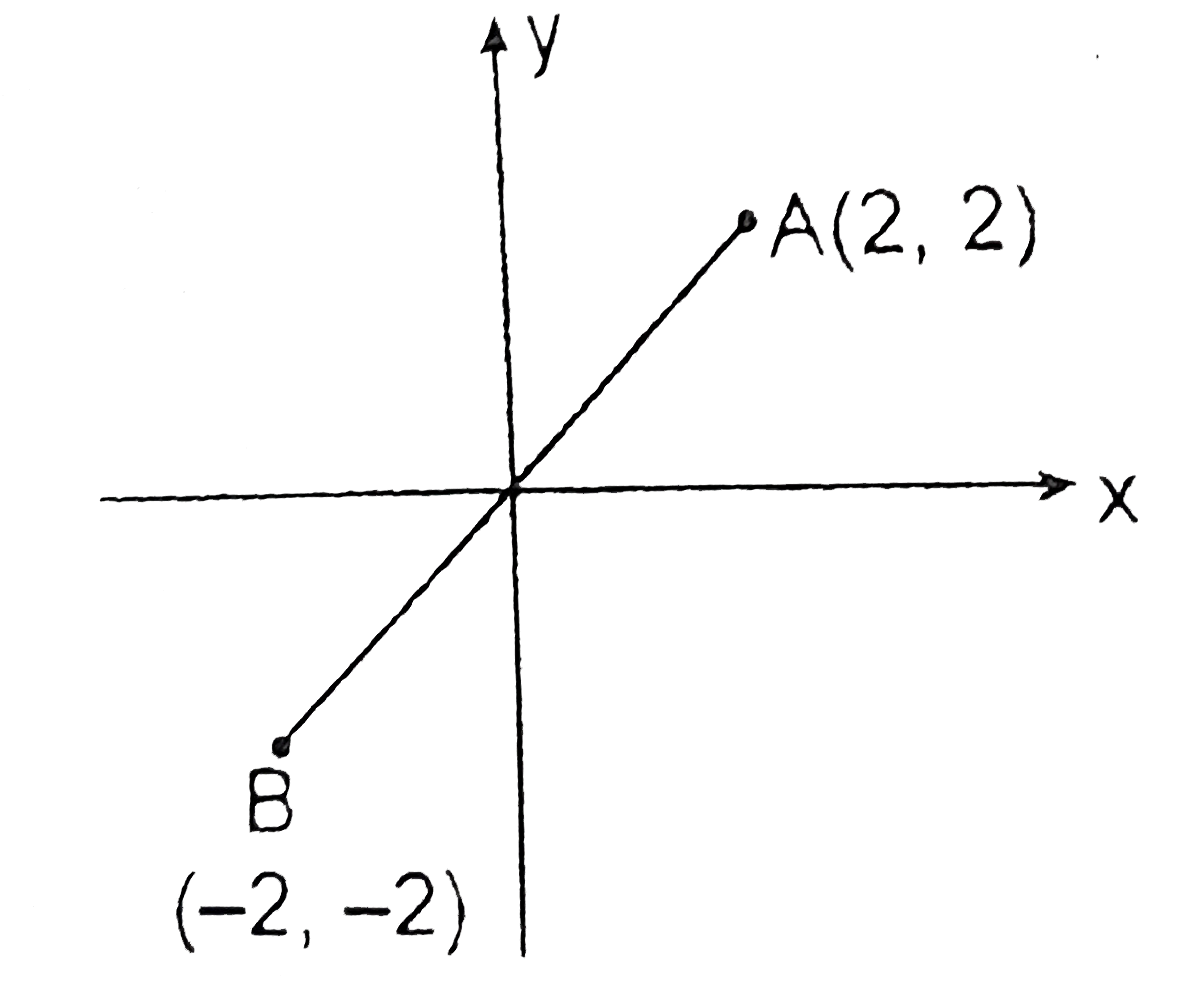
A particle of mass m=2kg executes SHM in xy- plane between point A and B under action of force →F=Fxˆi+Fyˆj. Minimum time taken by particle to move from A to B is 1 sec. At t=0 the particle is at x=2 and y=2. Then Fx as function of time t is
−4π2sinπt
−4π2cosπt
4π2cosπt
None of these
The correct Answer is:B
Let the line joining AB represents axis 'r' By the conditions given 'r' coordinates of the particle at time t is

r=2√2cosωt
⇒ω=2πT=2π2=π
∴R=2√2cosπt
x=rcos45∘=r√2=2cosπt
∴ax=−ω2x=−π22cosπt
∴Fx=max=−4π2cosπt.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.28
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.29
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMExercise:DPP No.26
Explore 8 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 19 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
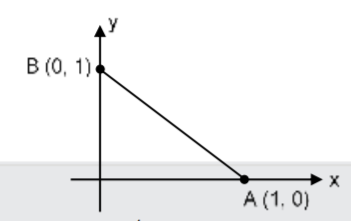
Particle moves from point A to point B along the line shown in figure under the action of force. VecF=−xˆi+yˆj. Determine the work done on the particle by →F in moving the particle from point A to point B.
View SolutionA particle of mass 2kg moves in the xy plane under the action of a constant force →F where →F=ˆi−ˆj. Initially the velocity of the particle is 2ˆj. The velocity of the particle at time t is
View SolutionParticle moves from point A to point B along the line shown in figure under the action of force. evcF=−xˆi+yˆj. Determine the work done on the particle by →F in moving the particle from point A to point B.

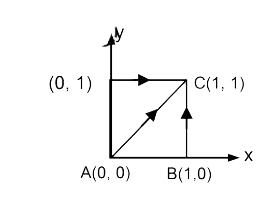
View SolutionA particle of mass m moves from A to C under the action of force →F=2xyˆi+y2ˆj , along different paths as shown in figure.
View SolutionA particle of mass 2 kg starts motion at time t = 0 under the action of variable force F = 4t (where F is in N and t is in s). The work done by this force in first two second is
View SolutionA particle is performing SHM of amplitude 'A' and time period 'T'. Find the time taken by the particle to go from 0→A/2.
View SolutionA particle of mass 0.1 kg executes SHM under a for F=(−10x) N. Speed of particle at mean position 6m/s. Then amplitude of oscillations is
View SolutionA particle moves in the x-y plane under the action of a force →F such that its linear momentum →P at any time t is →P=2costˆi+2sintˆj. The angle between →F and →P at a given time t will be
View SolutionA particle of mass 2kg is moving of a straight line under the action of force F=(8−2x)N. It is released at rest from x=6m.
a. Is the particle moving simple harmonically.
b. Find the equilibrium position of the particle.
c. Write the equation of motion of the particle.
d. Find the time period of SHM.
View SolutionA particle of mass 2kg starts to move at position x=0 and time t=0 under the action of force F=(10+4x)N along the x− axis on a frictionless horizontal track . Find the power delivered by the force in watts at the instant the particle has moved by distance 5m.
View Solution