Two particles move in a uniform gravitational field with an acceleration g. At the initial moment the particles were located over a tower at one point and moved with velocities v1=3m/sandv2=4m/s horizontally in opposite directions. Find the distance between the particles at the moment when their velocity vectors become mutually perpendicular.
The situation is shown fig.

Let the velocity vectors become perpendicular after time t when both particles has fallen same vertical distance 12gt2 and have acquired same vertical velocites gt.
Let their resultant velocities make angle θ1 and θ2 with horizontal.
Then tanθ1=gtv1 and tanθ2=gtv2
Since velocity vectors are perpendicular
θ1+θ2=90∘, hence tanθ2=cotθ1
It makes tanθ1=gtv1 and cotθ1=gtv2
On multiplying we get t=√v1v2g and D=(u1+u2)t
Similar Questions
Two particles move in a uniform gravitational field with an acceleration g. At the intial moment the particles were located at one point and moved with velocity v1=1 ms−1 and v2=4 ms−1 horizontally in opposite directions. Find the time interval after their velocity vectors become mutually perpendicular
View SolutionTwo particles are projected from a tower horizontally in opposite directions with velocities 10m/sand20m/s. Find the time when their velocity vectors are mutually perpendicular. Take g=10m/s2.
View SolutionA particle moves in a straight line with a uniform acceleration a. Initial velocity of the particle is zero. Find the average velocity of the particle in first 's' distance.
View SolutionTwo particles are moving with velocities v1andv2 . Their relative velocity is the maximum, when the angle between their velocities is
View SolutionTwo particles, 1 and 2, move with constant velocities v1 and v2 along two mutually perpendicular straight lines toward the intersection point O. At the moment t=0 the particles were located at the distances l1 and l2 from the point O. How soon will the distance between the particles become the smallest? What is it equal to?
View SolutionTwo particles are projected with speeds u1 and u2 in mutually opposite directions from top of a tower horizontally. Find the time after which their velocity becomes perpendicular to each other.
View SolutionA particle moves with a uniform velocity of 50 m/s for 20 min. What is the velocity of particle at t = 2 min ?
View SolutionA particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionA particle starts from the point (0m,8m) and moves with uniform velocity of 3ˆim/s. After 5 seconds, the angular velocity of the particle about the origin will be :
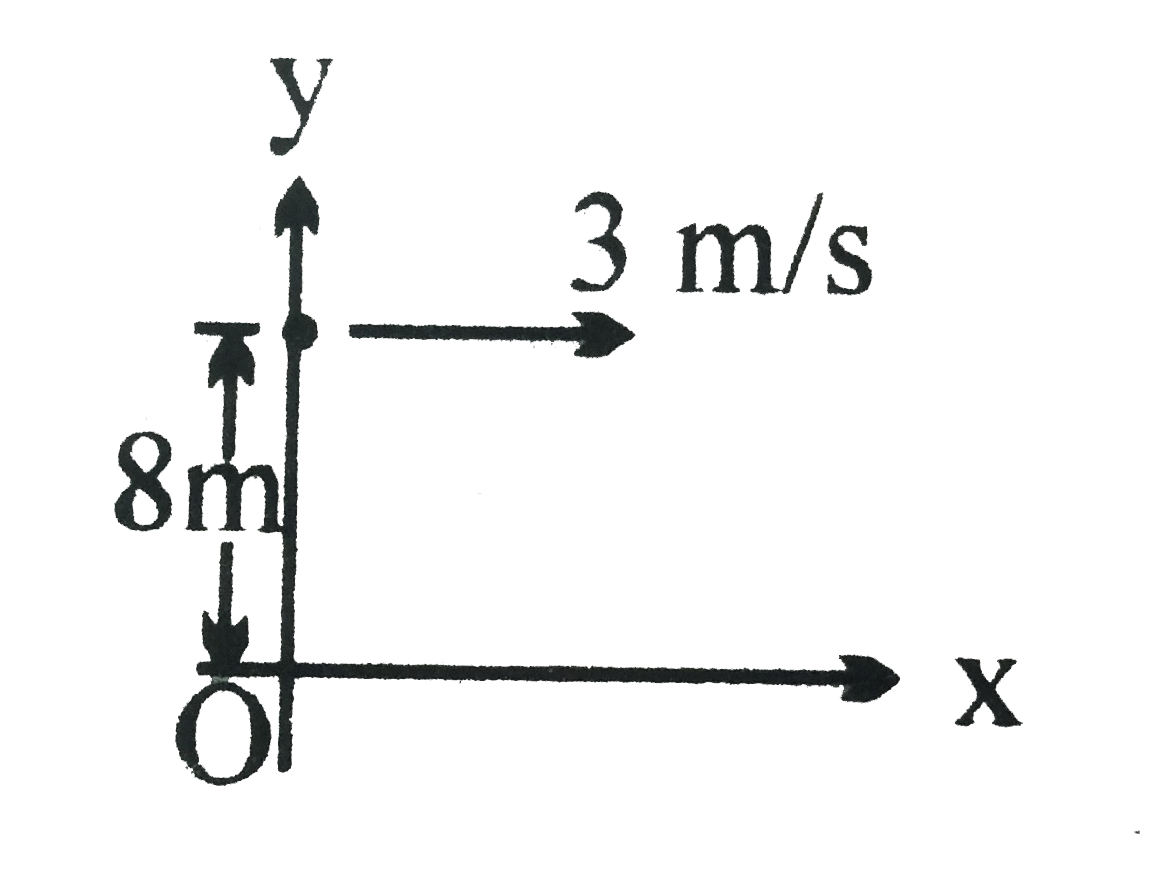 .
.
View SolutionA particle moving along a straight line with a constant acceleration of −4m/s2 passes through a point A on the line with a velocity of +8m/s at some moment. Find the distance travelled by the particle in 5 seconds after that moment.
View Solution
