A charge Q is kept at the centre of a circle of radius 'r' If permittivity of the free space is e, then work done in carrying a charge q along the diameter of the circle from one end to the other will be
A) qQ4π∈0∈rr
B) qQ8π∈0r
C) qQ2π∈0
D) zero
The correct Answer is:D
To solve the problem, we need to determine the work done in moving a charge q from one end of the diameter of a circle to the other end, with a charge Q located at the center of the circle.
1. Understanding the Setup:
- We have a charge Q at the center of a circle with radius r.
- We want to move a charge q from point A to point B along the diameter of the circle.
2. Electric Potential Due to Charge Q:
- The electric potential V at a distance r from a point charge Q is given by the formula:
V=Q4πϵr
- Since charge q is moved along the diameter, the distance from the charge Q to any point on the diameter remains constant (equal to r).
3. Equipotential Surface:
- The charge Q creates an equipotential surface around it. This means that the potential is the same at all points equidistant from the charge.
- Therefore, the potential at point A (one end of the diameter) is equal to the potential at point B (the other end of the diameter):
VA=VB
4. Work Done Calculation:
- The work done W in moving a charge in an electric field is given by the formula:
W=q(VB−VA)
- Since VA=VB, we have:
W=q(0)=0
5. Conclusion:
- The work done in carrying the charge q along the diameter of the circle from one end to the other is:
W=0
Final Answer:
The work done in carrying a charge q along the diameter of the circle from one end to the other is 0.
- We have a charge Q at the center of a circle with radius r.
- We want to move a charge q from point A to point B along the diameter of the circle.
- The electric potential V at a distance r from a point charge Q is given by the formula:
V=Q4πϵr
- Since charge q is moved along the diameter, the distance from the charge Q to any point on the diameter remains constant (equal to r).
- The charge Q creates an equipotential surface around it. This means that the potential is the same at all points equidistant from the charge.
- Therefore, the potential at point A (one end of the diameter) is equal to the potential at point B (the other end of the diameter):
VA=VB
- The work done W in moving a charge in an electric field is given by the formula:
W=q(VB−VA)
- Since VA=VB, we have:
W=q(0)=0
- The work done in carrying the charge q along the diameter of the circle from one end to the other is:
W=0
The work done in carrying a charge q along the diameter of the circle from one end to the other is 0.
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (CUTTENT ELECTRICITY )
108 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
95 Videos
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )
52 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
24 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
Similar Questions
Charge q2 is at the centre of a circular path with radius r. work done in carrying charge q1 once around this equipotential path , would be
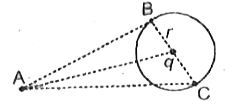
View SolutionA point charge q is held at the centre of a circle of radius r. B,C are two points on the circumference of the circle and A is a point outsdie the circle . If WAB charge qe from A to B and WAC represents the workdone from A to C ,then
View Solution
Knowledge Check
The work done in carrying a charge q once round a circle of radius r with a charge Q at the centre is
AqQ4πε0aBqQ4πε0a2Cq4πε0aDzeroThe work done to move a unit charge along an equipotential from P to Q
Amust be defined as −Q∫P→E.→dlBis zeroCcan have a non-zero valueDboth (a) and (b)are correct
a. A circle is drawn with center as a charge +q. What is the work done in moving a charge +q from B to C along the circumferebce of the circle ?
B In the above question, if the charge +q is first taken from B to A and then from A to C, on which path is the magnitude of work greater?
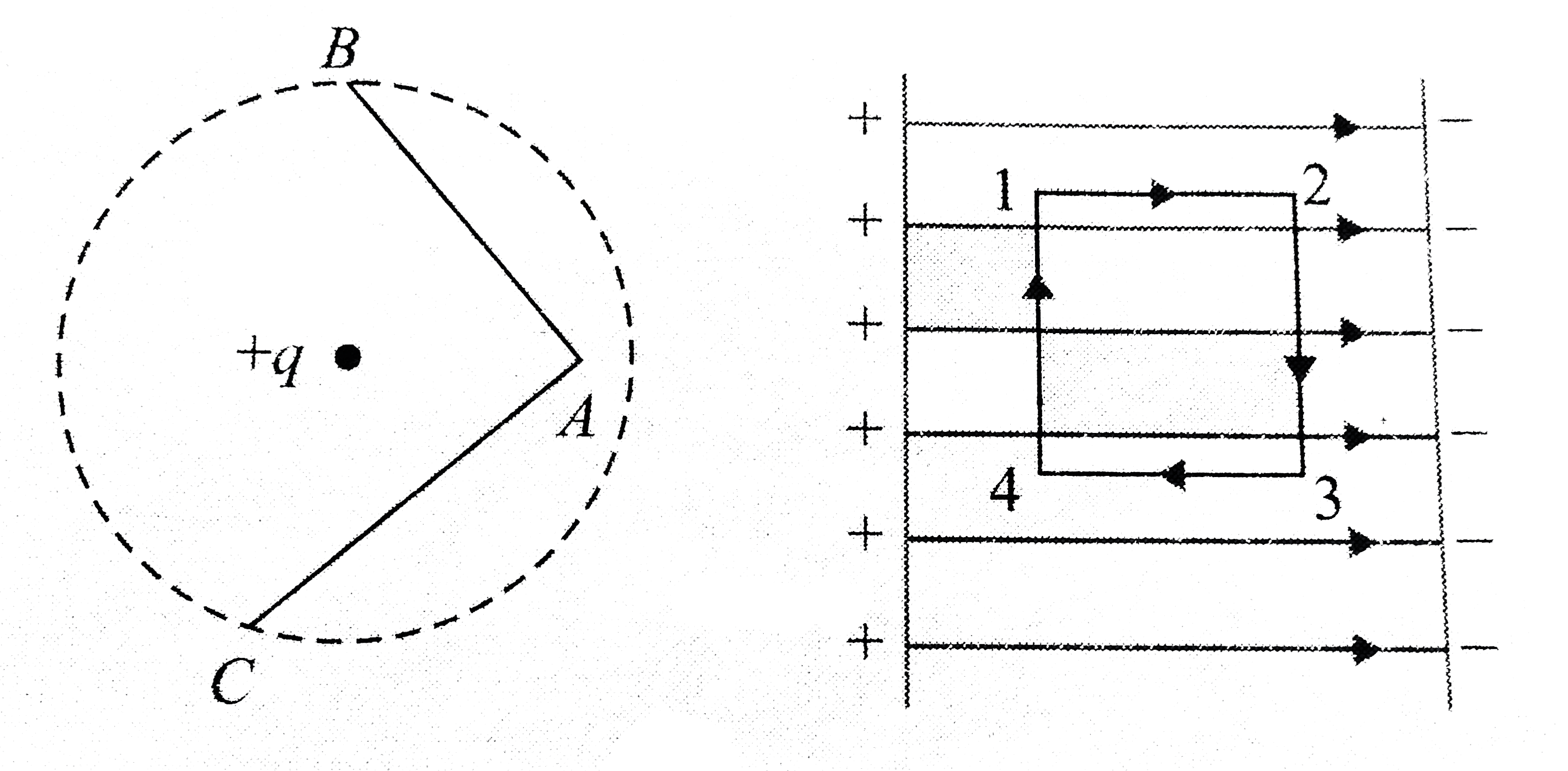
View SolutionTwo identical thin ring, each of radius R meters, are coaxially placed a distance R metres apart. If Q1 coulomb, and Q2 coulomb, are repectively the charges uniformly spread on the two rings, the work done in moving a charge q from the centre of one ring to that of the other is
View SolutionTwo identical thin ring, each of radius R meters, are coaxially placed a distance R metres apart. If Q1 coulomb, and Q2 coulomb, are repectively the charges uniformly spread on the two rings, the work done in moving a charge q from the centre of one ring to that of the other is
View SolutionA charge Q is placed at the origin. The electric potential due to this charge at a given point in space is V. The work done by an external force in bringing another charge q from infinity up to the point is
View SolutionA charge -q is placed at the axis of a charged ring of radius at a distance of 2√2 r as show in figure . If ring is fixed and carrying charge Q, the kinetic energy of charge - q when it is relased and reaches the centre of ring will be qQnπε0r.Find n

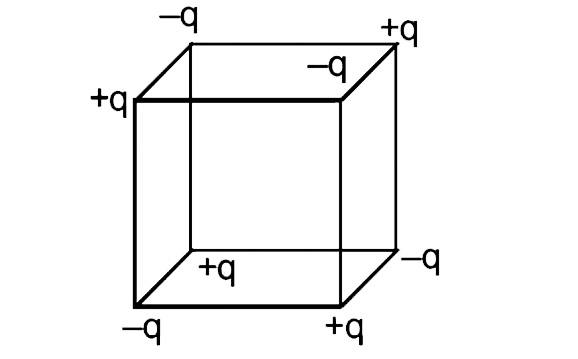
View SolutionCharges +q and −q are located at the corners of a cube of side as show in the figure. Find the work done to separate the charges to infinite distance
View Solution
