A small bulb is placed at a depth of 2√7 m in water and floating opaque disc is placed over the bulb so that bulb is not visible from the surface. The minimum diameter of the disc is (μwater=4/3)
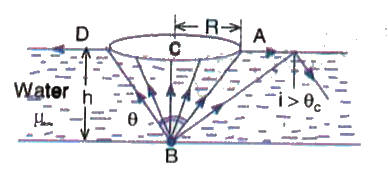
As shown in figure, light from bulb will not emerge out of water if at the edge of disc,
i>θcorsinθc
Now if R is the radius of disc and h is the depth of bulb from it, sini=R√R2+h2 and sinθc=1μ
So equation (1) becomes
R√R2+h2>1μorR>h√μ2−1
here h=2√7mandμ=(4/3)
So Rmin=2√7√(16/9)−1=6m
So diameter of disc = 2R = 2 × 6 = 12 m
Topper's Solved these Questions
- RAY OPTICSBook:AAKASH SERIESChapter:RAY OPTICSExercise:EXERCISE (LONG ANSWER QUESTIONS )
Explore 9 Videos
- RAY OPTICSBook:AAKASH SERIESChapter:RAY OPTICSExercise:EXERCISE (SHORT ANSWER QUESTIONS )
Explore 24 Videos
- PRACTICAL PHYSICSBook:AAKASH SERIESChapter:PRACTICAL PHYSICSExercise:LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions
Explore 4 Videos
- SEMICONDUCTOR DEVICESBook:AAKASH SERIESChapter:SEMICONDUCTOR DEVICESExercise:EXERCISE - III
Explore 3 Videos
Similar Questions
A bulb is placed at a depth of 2√7cm in water and a floating opaque disc is placed over the bulb so that the bulb is not visible from the surface. What is the minimum diameter of the disc?
View SolutionAn isotropic point source is placed at a depth h below the water surface. A floating opaque disc is placed on the surface of water so that the source is not visible from the surface. What is the minimum radius of the disc? Take refractive index of water=μ.
View Solution
Knowledge Check
A point source of light is placed at a depth of h below the surface of water of refractive index μ. A floating opaque disc is placed on the surface of water so that light from the source is not visible from the surface. The minimum diameter of the disc is
A2h(μ2−1)1/2B2h(μ2−1)1/2Ch2(μ2−1)1/2Dh(μ2−1)1/2
An isotropic point source is placed at a depth h below the water surface. A floating opaque disc is placed on the surface of water so that the source is not visible from the surface. What is the minimum radius of the disc? Take refractive index of water=μ.
View SolutionA point source is placed at a depth h below the surface of water (refractive index =μ). The medium above the surface area of water is air from water.
View SolutionA point object is placed at a distance of 20 cm from a glass slab, H=18cm, half immersed in water as shown in figure. The distance between two images when seen from the other side of the slab is (μg=32andμw=43)
View SolutionA disc is placed on a surface of pond which has refractive index 35 . A source of light is placed 4 m below the surface of liquid. The minimum radius of disc will be so light is not coming out
View SolutionAn under water swimmer is at a depth of 12 m below the surface of water. A bird is at a height of 18 m from the surface of water, directly above his eyes. For the swimmer the bird appears to be at a distance from the surface of water equal to (Refractive Index of water is 4/3)
View SolutionA cylindrical vessel, whose diameter and height both are equal to 30 cm, is placed on a horizontal surface and a small particle P is placed in it at a distance of 5.0 cm from the centre. An eye is placed at a position such that the edge of the bottom is just visible (see figure 18-E8). The particle P is in the plane of drawing. Up to what minimum height should water be poured in the vessel to make the particle P visible ?

View SolutionA disc is placed on the surface of pond filled with liquid of refractive index 53. A source of light is placed 4m below the surface of liquid. Calculate the minimum area of the disc so that light does not come out of liquid.
View Solution