A beam of 30 MeV α particles is to be obtained from a cyclotron of radius 50cm . The strength of magnetic field required to be applied will be
1.582 T
0.01582 T
0.1582 T
15.82 T
The correct Answer is:A
To find the strength of the magnetic field required to accelerate a beam of 30 MeV alpha particles in a cyclotron of radius 50 cm, we can follow these steps:
Step 1: Understand the relationship in a cyclotron
The radius r of the cyclotron is given by the formula:
r=mvqB
where:
- m = mass of the particle
- v = velocity of the particle
- q = charge of the particle
- B = magnetic field strength
Step 2: Calculate the kinetic energy in joules
The kinetic energy K.E. of the alpha particles is given as 30 MeV. We need to convert this into joules:
K.E.=30MeV=30×106eV=30×106×1.6×10−19J=4.8×10−12J
Step 3: Find the velocity of the alpha particles
We can use the kinetic energy formula:
K.E.=12mv2
From this, we can solve for v:
v=√2×K.E.m
Step 4: Determine the mass of the alpha particle
The mass of an alpha particle is approximately 4 times the mass of a proton:
m=4×(1.67×10−27kg)=6.68×10−27kg
Step 5: Substitute values to find velocity
Substituting the values into the velocity equation:
v=√2×4.8×10−126.68×10−27
Step 6: Calculate the velocity
Calculating the above expression gives:
v≈√9.6×10−126.68×10−27≈√1.44×1015≈1.2×107m/s
Step 7: Determine the charge of the alpha particle
The charge of an alpha particle is twice the charge of a proton:
q=2×(1.6×10−19C)=3.2×10−19C
Step 8: Rearrange the cyclotron formula to find B
Rearranging the formula for B:
B=mvqr
Step 9: Substitute all known values
Substituting the known values into the equation:
- m=6.68×10−27kg
- v=1.2×107m/s
- q=3.2×10−19C
- r=0.5m
B=(6.68×10−27)(1.2×107)(3.2×10−19)(0.5)
Step 10: Calculate B
Calculating the above expression gives:
B≈8.016×10−201.6×10−19≈0.501T≈1.5T
Final Answer
The strength of the magnetic field required is approximately:
B≈1.5T
The radius r of the cyclotron is given by the formula:
r=mvqB
where:
- m = mass of the particle
- v = velocity of the particle
- q = charge of the particle
- B = magnetic field strength
The kinetic energy K.E. of the alpha particles is given as 30 MeV. We need to convert this into joules:
K.E.=30MeV=30×106eV=30×106×1.6×10−19J=4.8×10−12J
We can use the kinetic energy formula:
K.E.=12mv2
From this, we can solve for v:
v=√2×K.E.m
The mass of an alpha particle is approximately 4 times the mass of a proton:
m=4×(1.67×10−27kg)=6.68×10−27kg
Substituting the values into the velocity equation:
v=√2×4.8×10−126.68×10−27
Calculating the above expression gives:
v≈√9.6×10−126.68×10−27≈√1.44×1015≈1.2×107m/s
The charge of an alpha particle is twice the charge of a proton:
q=2×(1.6×10−19C)=3.2×10−19C
Rearranging the formula for B:
B=mvqr
Substituting the known values into the equation:
- m=6.68×10−27kg
- v=1.2×107m/s
- q=3.2×10−19C
- r=0.5m
Calculating the above expression gives:
B≈8.016×10−201.6×10−19≈0.501T≈1.5T
The strength of the magnetic field required is approximately:
B≈1.5T
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-III
Explore 49 Videos
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-IB
Explore 71 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:very Short answer type question
Explore 15 Videos
- NUCLEAR PHYSICSBook:AAKASH SERIESChapter:NUCLEAR PHYSICSExercise:ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
Explore 3 Videos
Similar Questions
The momentum of α-particles moving in a circular path of radius 10 cm in a perpendicular magnetic field of 0.05 tesla will be :
View SolutionA α -parhticle moves in a circular path of radius 0.83cm in the presence of a magnetic field of 0.25Wb/m2. The de-Broglie wavelength assocaiated with the particle will be
View Solution
Knowledge Check
A α -parhticle moves in a circular path of radius 0.83cm in the presence of a magnetic field of 0.25Wb/m2. The de-Broglie wavelength assocaiated with the particle will be
A1Ã…B0.1Ã…C10Ã…D0.01Ã…
A beam of α particles projected along + x-axis, experiences a force due to a magnetic field along the +y-axis figure. What is the direction of magnetic field.
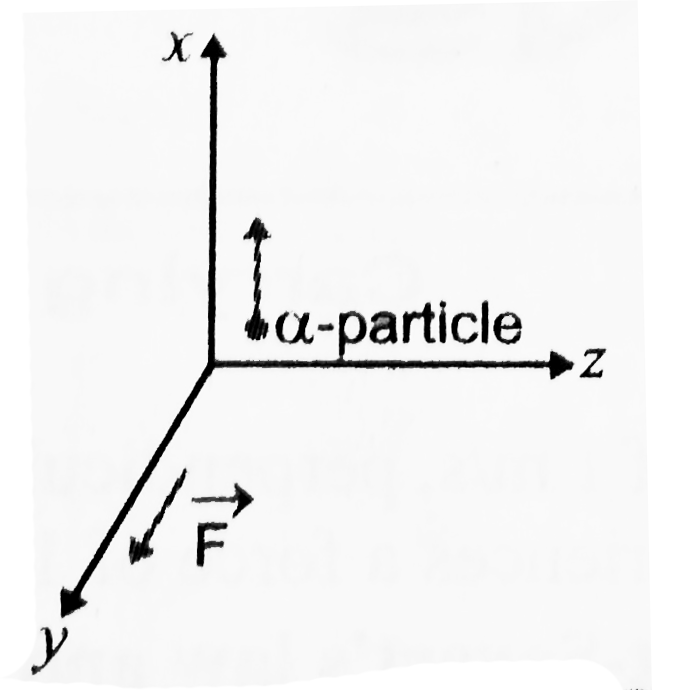
View SolutionA particle having a charge20μC and mass 20μg moves along a circle of radius 5.0 cm under the action of a magnetic field 5.0 cm under the action of a magnetic field B = 1.0 T. When the particle is at a point P, a uniform electric field is switched on and it is found that the particla continues on the tangent through P qith a uniform velocity. Find the electric field.
View SolutionA particle of mass m having a charge q enters into a circular region of radius R with velocity v directed towards the centre. The strength of magnetic field is B. Find the deviation in the path of the particle.
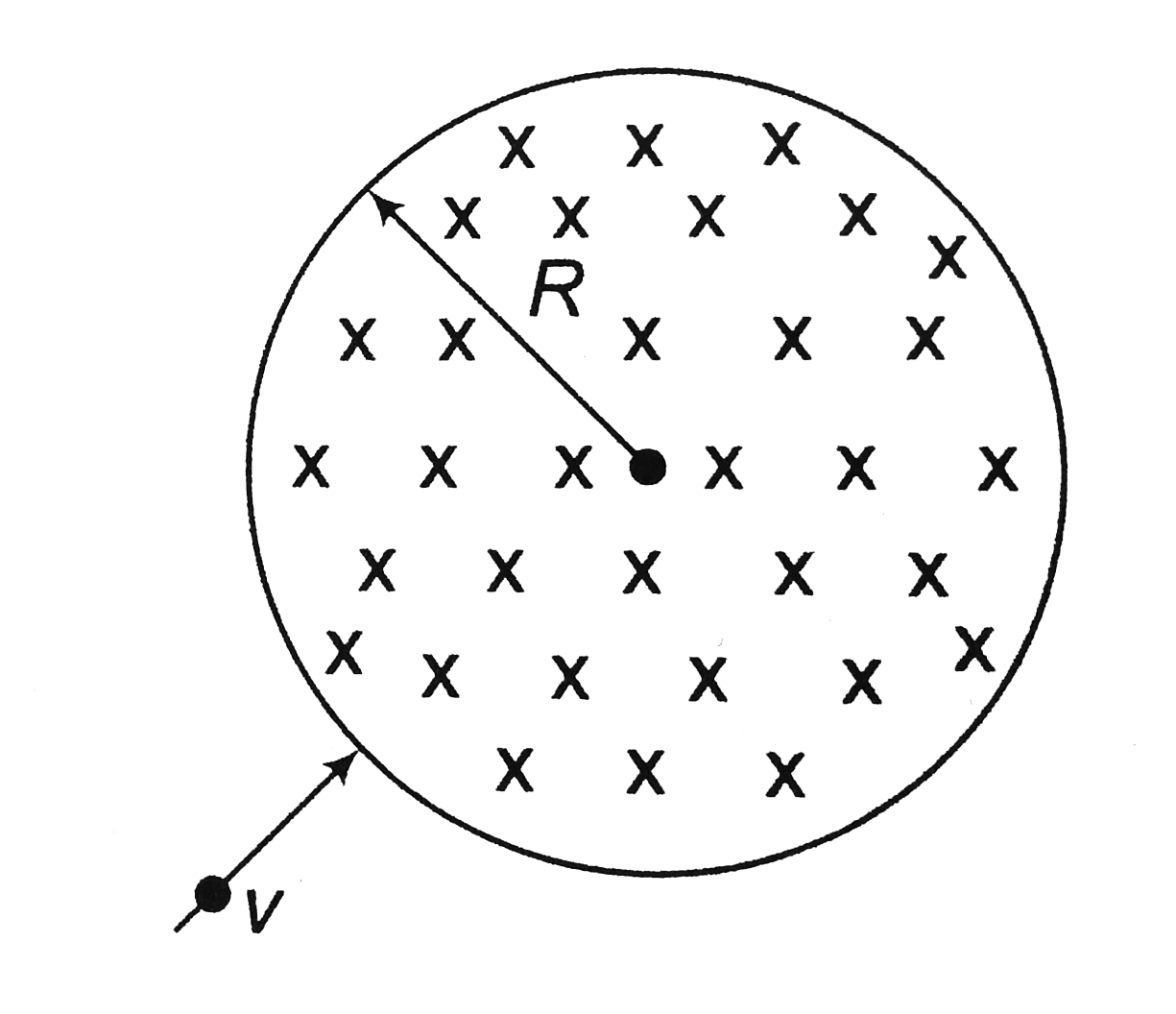
View SolutionIf an alpha particle and a proton are accelerated from rest by a potential difference of 1MeV, then the ratio of their kinetic energies will be
View SolutionA beam of mixture of α particle and protons are accelerted through same potential difference before entering into the magnetic field of strength B. if r1=5 cm then r2 is

View SolutionThe magnetic flux density applied in a cyclotron is 3⋅5T. What will be the frequency of electric field that must be applied between the dees in order (a) to accelerate protons (b) α-particles? mass of proton 1⋅67×10−27kg.
View SolutionThe cyclotron is a device which is used to accelerate charged particles such as protons, deutrons, alpha particles, etc. to very high energy. The principle on which a cyclotron works is based on the fact that an electric field can accelerate a charged particle and a magnetic field can throw it into a circular orbit. A particle of charge +q experiences a force qE in an electric field E and this force is independent of velocity of the particle. The particle is accelerated in the direction of the magnetic field. On the other hand, a magnetic field at right angles to the direction of motion of the particle throws the particle in a circular orbit in which the particle revolves with a frequency that does not depend on its speed. A modest potential difference is used as a sources of electric field. If a charged particle is made to pass through this potential difference a number of times, it will acquire an enormous by large velocity and hence kinetic energy.
Which of the following cannot be accelerated in a cyclotron?
View Solution

