A circular arc of wire subtends an angle /2 at the centre. If it carries a current i and its radius of curvature is R then the magnetic field at the centre of the arc is
The correct Answer is:D
To solve the problem of finding the magnetic field at the center of a circular arc of wire that subtends an angle of π2 at the center, we can follow these steps:
1. Identify the Formula:
The magnetic field B at the center of a circular arc carrying current i and subtending an angle θ is given by the formula:
B=μ0i4πr⋅θ
where:
- B is the magnetic field,
- μ0 is the permeability of free space,
- i is the current,
- r is the radius of the arc,
- θ is the angle in radians.
2. Substitute the Given Values:
In this case, we have:
- θ=π2,
- r=R (the radius of curvature).
Plugging these values into the formula:
B=μ0i4πR⋅π2
3. Simplify the Expression:
Now, simplify the expression:
B=μ0i⋅π4πR⋅2
This simplifies to:
B=μ0i8R
4. Final Result:
Thus, the magnetic field at the center of the arc is:
B=μ0i8R
Conclusion:
The magnetic field at the center of the circular arc is given by:
B=μ0i8R
The magnetic field B at the center of a circular arc carrying current i and subtending an angle θ is given by the formula:
B=μ0i4πr⋅θ
where:
- B is the magnetic field,
- μ0 is the permeability of free space,
- i is the current,
- r is the radius of the arc,
- θ is the angle in radians.
In this case, we have:
- θ=π2,
- r=R (the radius of curvature).
B=μ0i4πR⋅π2
Now, simplify the expression:
B=μ0i⋅π4πR⋅2
This simplifies to:
B=μ0i8R
Thus, the magnetic field at the center of the arc is:
B=μ0i8R
The magnetic field at the center of the circular arc is given by:
B=μ0i8R
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-III
Explore 49 Videos
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-IB
Explore 71 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:very Short answer type question
Explore 15 Videos
- NUCLEAR PHYSICSBook:AAKASH SERIESChapter:NUCLEAR PHYSICSExercise:ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
Explore 3 Videos
Similar Questions
The magnetic field at centre O of the arc in Fig.
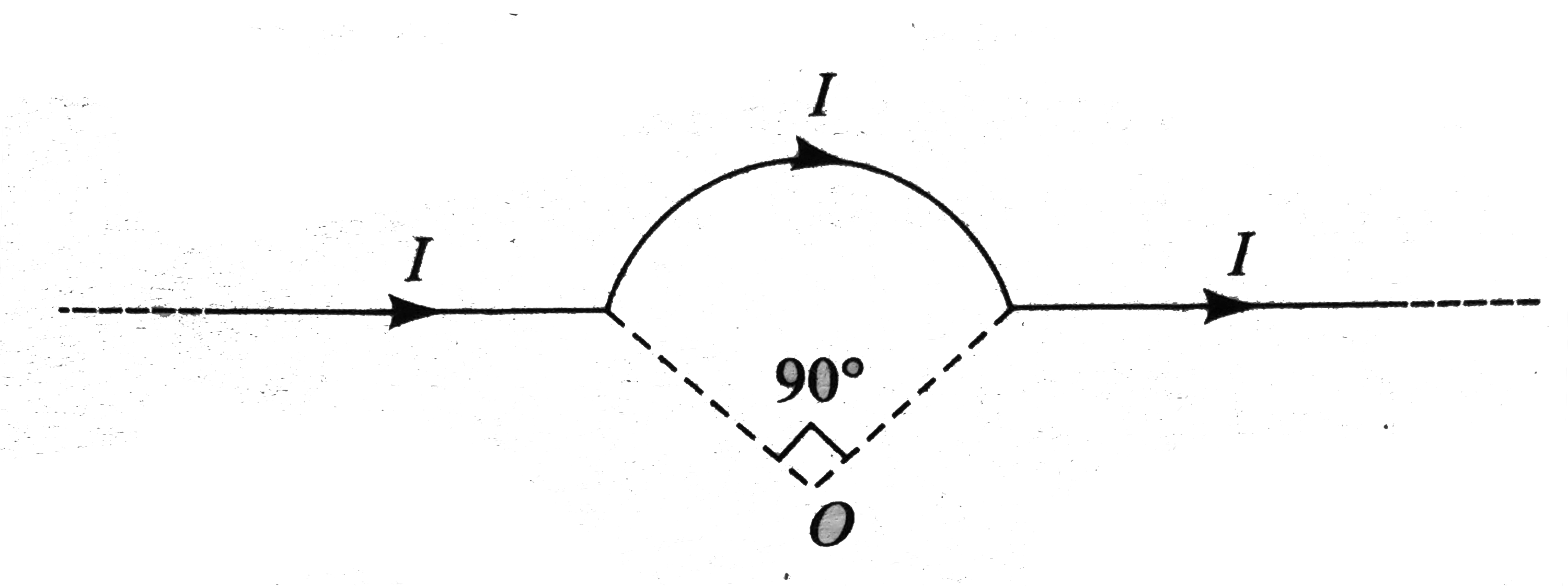
View SolutionAn arc of a circle of raduis R subtends an angle π2 at the centre. It carriers a current i. The magnetic field at the centre will be
View SolutionA circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
View SolutionAn arc of length 20π cm subtends an angle of 144o at the centre of a circle. Find the radius of the circle.
View Solution
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius R
View SolutionA long wire bent as shown in fig. carries current I. If the radius of the semicircular portion is a, the magnetic field at centre C is

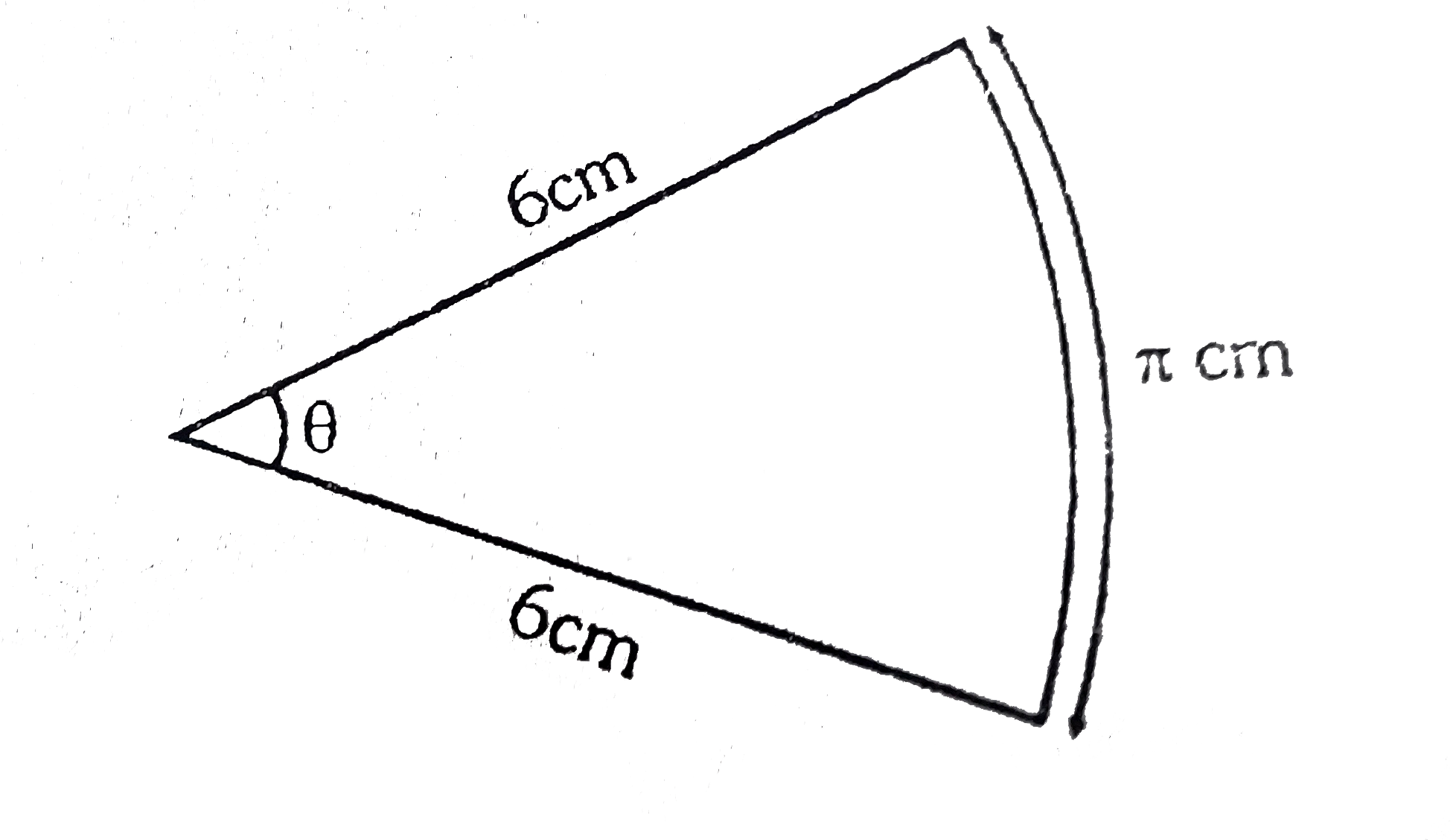
View SolutionA circular arc of length π cm. Find angle subtended by it at the centre in radian and degree.
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :

View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

View SolutionA wire of length 'I' is bent into a circular loop of radius R and carries a current I. The magnetic field at the centre of the loop is 'B '. The same wire is now bent into a double loop. If both loops carry the same current I and it is in the same direction, the magnetic field at the centre of the double loop will be
View Solution

