A wire of length 'I' is bent into a circular loop of radius R and carries a current I. The magnetic field at the centre of the loop is 'B '. The same wire is now bent into a double loop. If both loops carry the same current I and it is in the same direction, the magnetic field at the centre of the double loop will be
zero
2B
4B
8B
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Understand the Magnetic Field due to a Single Loop
The magnetic field B at the center of a circular loop of radius R carrying a current I is given by the formula:
B=μ0I2R
where μ0 is the permeability of free space.
Step 2: Relate the Length of the Wire to the Radius of the Loop
The length of the wire L is equal to the circumference of the loop:
L=2πR
From this, we can express the radius R in terms of the length of the wire:
R=L2π
Step 3: Substitute R into the Magnetic Field Formula
Substituting R into the magnetic field formula gives:
B=μ0I2(L2π)=μ0I⋅2π2L=μ0πIL
Step 4: Analyze the Double Loop Configuration
When the wire is bent into a double loop, the total length of the wire remains the same, L, but now it forms two loops. Therefore, the length of wire for each loop is:
L′=L2
The radius for each loop in the double loop configuration can be calculated as:
2πR′=L2⟹R′=L4π
Step 5: Calculate the Magnetic Field for the Double Loop
The magnetic field at the center of the double loop is given by:
B′=2⋅μ0I2R′=μ0IR′
Substituting R′:
B′=μ0IL4π=4πμ0IL
Step 6: Relate B′ to B
Now we can relate B′ to B:
B′=4πμ0IL=4(μ0πIL)=4B
Conclusion
The magnetic field at the center of the double loop is:
B′=4B
The magnetic field B at the center of a circular loop of radius R carrying a current I is given by the formula:
B=μ0I2R
where μ0 is the permeability of free space.
The length of the wire L is equal to the circumference of the loop:
L=2πR
From this, we can express the radius R in terms of the length of the wire:
R=L2π
Substituting R into the magnetic field formula gives:
B=μ0I2(L2π)=μ0I⋅2π2L=μ0πIL
When the wire is bent into a double loop, the total length of the wire remains the same, L, but now it forms two loops. Therefore, the length of wire for each loop is:
L′=L2
The radius for each loop in the double loop configuration can be calculated as:
2πR′=L2⟹R′=L4π
The magnetic field at the center of the double loop is given by:
B′=2⋅μ0I2R′=μ0IR′
Substituting R′:
B′=μ0IL4π=4πμ0IL
Now we can relate B′ to B:
B′=4πμ0IL=4(μ0πIL)=4B
The magnetic field at the center of the double loop is:
B′=4B
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
49 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB
71 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
- NUCLEAR PHYSICSBOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
3 Videos
Similar Questions
A square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View SolutionA rectangular loop of metallic wire is of length a and breadth b and carries a current i. The magnetic field at the centre of the loop is
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is (dependence on L)
View SolutionOn meter length of wires carriers a constant current. The wire is bent to from a circular loop. The magnetic field at the centre of this loop is B. The same is now bent to form a circular loop of smaller radius to have four turns in the loop. The magnetic field at the centre of this loop B. The same is now bent to form a circular loop of smaller radius of have four turns in the loop. The magnetic field at the centre of this new loop is
View SolutionA wire of length l carries a steady current. It is bent first to form a circular plane loop of one turn. The magnetic field at the centre of the loop is B. The same length is now bent more sharply to give a double loop of smaller radius. The magnetic field at the centre caused by the same is
View SolutionA long wire having a semi-circular loop of radius r carries a current I, as shown in Fig. Find the magnetic field due to entire wire.

View SolutionA circular loop of one turn carries a current of 5.00 A. If the magnetic field B at the centre is 0.200 mT, find the radius of the loop.
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
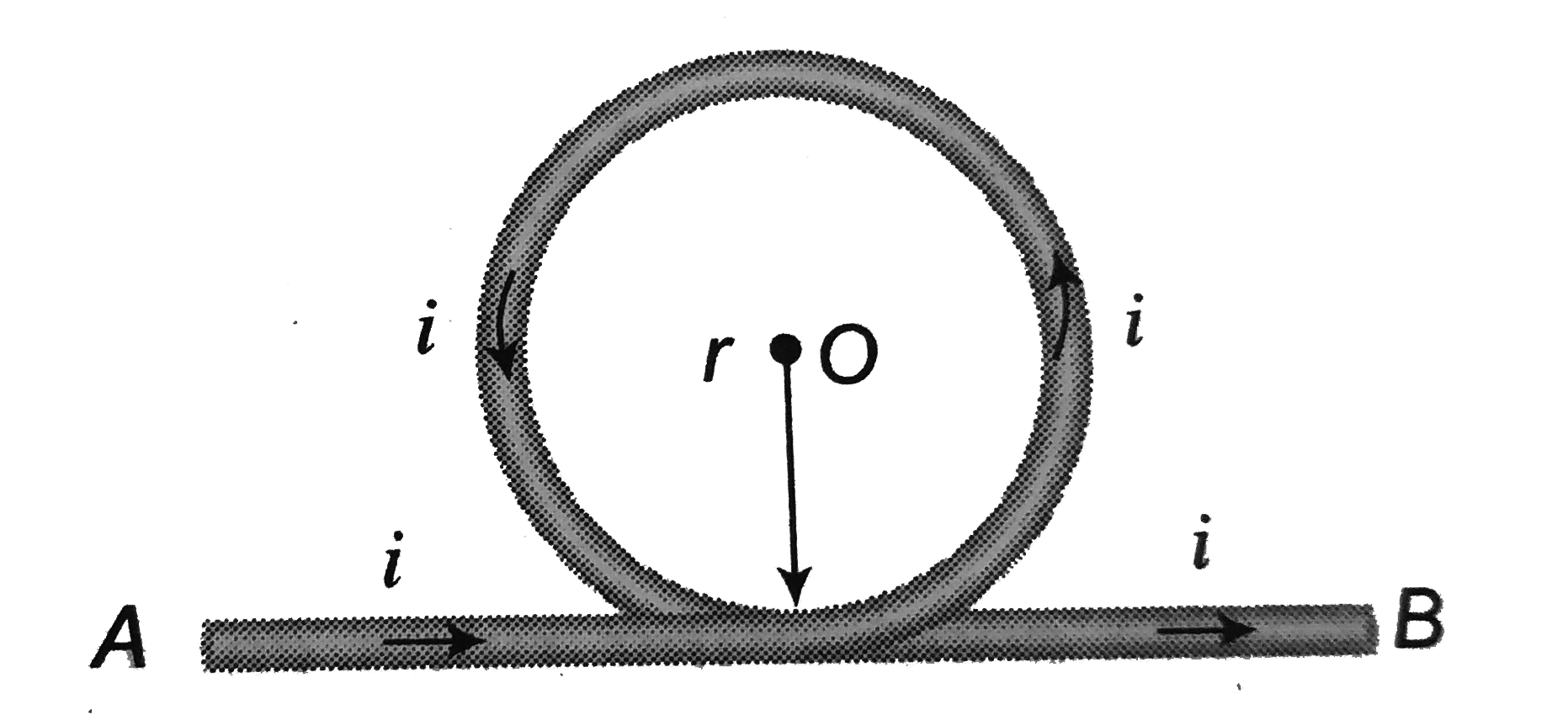
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :

View Solution
