A proton enters a magnetic field of flux density 1.5 T with a velocity of 2×107ms−1 at an angle of 30° with the field. The force on the proton is [ep=1.6×10−19C]
2.4×10−12N
2.4×10−11N
3×10−5N
3×10−4N
The correct Answer is:B
To find the magnetic force on a proton entering a magnetic field, we can use the formula for the magnetic force acting on a charged particle:
FB=qvBsinθ
Where:
- FB is the magnetic force,
- q is the charge of the particle,
- v is the velocity of the particle,
- B is the magnetic flux density,
- θ is the angle between the velocity and the magnetic field.
1. Identify the given values:
- Charge of the proton, q=1.6×10−19C
- Velocity of the proton, v=2×107m/s
- Magnetic flux density, B=1.5T
- Angle, θ=30∘
2. Substitute the known values into the formula:
FB=(1.6×10−19)×(2×107)×(1.5)×sin(30∘)
3. Calculate sin(30∘):
sin(30∘)=12
4. Substitute sin(30∘) into the equation:
FB=(1.6×10−19)×(2×107)×(1.5)×(12)
5. Simplify the expression:
FB=(1.6×10−19)×(2×107)×(0.75)
6. Calculate the product:
- First, calculate 1.6×2=3.2
- Then, 3.2×0.75=2.4
- Finally, combine with 10−19×107=10−12
Thus,
FB=2.4×10−12N
Final Answer:
The magnetic force on the proton is FB=2.4×10−12N.
---
- FB is the magnetic force,
- q is the charge of the particle,
- v is the velocity of the particle,
- B is the magnetic flux density,
- θ is the angle between the velocity and the magnetic field.
- Charge of the proton, q=1.6×10−19C
- Velocity of the proton, v=2×107m/s
- Magnetic flux density, B=1.5T
- Angle, θ=30∘
FB=(1.6×10−19)×(2×107)×(1.5)×sin(30∘)
sin(30∘)=12
FB=(1.6×10−19)×(2×107)×(1.5)×(12)
FB=(1.6×10−19)×(2×107)×(0.75)
- First, calculate 1.6×2=3.2
- Then, 3.2×0.75=2.4
- Finally, combine with 10−19×107=10−12
FB=2.4×10−12N
The magnetic force on the proton is FB=2.4×10−12N.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-III
Explore 49 Videos
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-IB
Explore 71 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:very Short answer type question
Explore 15 Videos
- NUCLEAR PHYSICSBook:AAKASH SERIESChapter:NUCLEAR PHYSICSExercise:ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
Explore 3 Videos
Similar Questions
A proton enters a magnetic field of flux density 1.5 T with a velocity of 2×107ms−1 at an angle of 30° with the field. The force on the proton is [ep=1.6×10−19C]
View SolutionA proton moving withh a velocity 2.5×107m/s enters a magnetic field of intensity 2.5T making an angle 30∘ with the magnetic field. The force on the proton is
View SolutionA beam of protons enters a uniform magnetic field of 0.3T with velocity of 4×105m/s in a direction making an angle of 60∘ with the direction of magnetic field. The path of motion of the particle will be
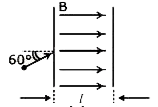
View SolutionThe figure shows a region of length ‘l’ with a uniform magnetic field of 0.3 T in it and a proton entering the region with velocity 4×105 ms−1 making an angle 60∘ with the field. If the proton completes 10 revolution by the time it cross the region shown, ‘l’ is close to (mass of proton =1.67×10−27 kg , charge of the proton =1.6×10−19 C )
View SolutionA beam of protons moving with a velocity of 4×105ms enters a uniform magnetic field of 0.3 T at an angle of 60◦ with the magnetic field. What is the radius of the helical path described by the proton beam?[mp=1.67×10−27kg and the charge on the proton=1.6×10−19C]
View SolutionA proton enter in a uniform magnetic field of 2.0 mT at an angle of 60degrees with the magnetic field with speed 10m/s. Find the picth of path
View SolutionA proton moves with a speed of 2.0×107ms−1 along the x -axis.It enters a region where there is a magnetic field of magnitude 1.5T directed at an angle of 30∘ to the x -axis and lying in the xy plane.The magnitude of the magnetic force on the proton is
View SolutionA beam of protons with a velocity of 4X105ms−1 enters a uniform magnetic field of 0.3 T. The velocity makes an angle of 60∘ with the magnetic field. Find the radius of the helical path taken by the proton beam.
View SolutionA beam of protons with a velocity of 4X105ms−1 enters a uniform magnetic field of 0.3 T. The velocity makes an angle of 60∘ with the magnetic field. Find the radius of the helicla path taken by the proton beam and the pitch of the helix.
View SolutionA beam of protons with a velocity of 4X105ms−1 enters a uniform magnetic field of 0.3 T. The velocity makes an angle of 60∘ with the magnetic field. Find the radius of the helicla path taken by the proton beam and the pitch of the helix.
View Solution

