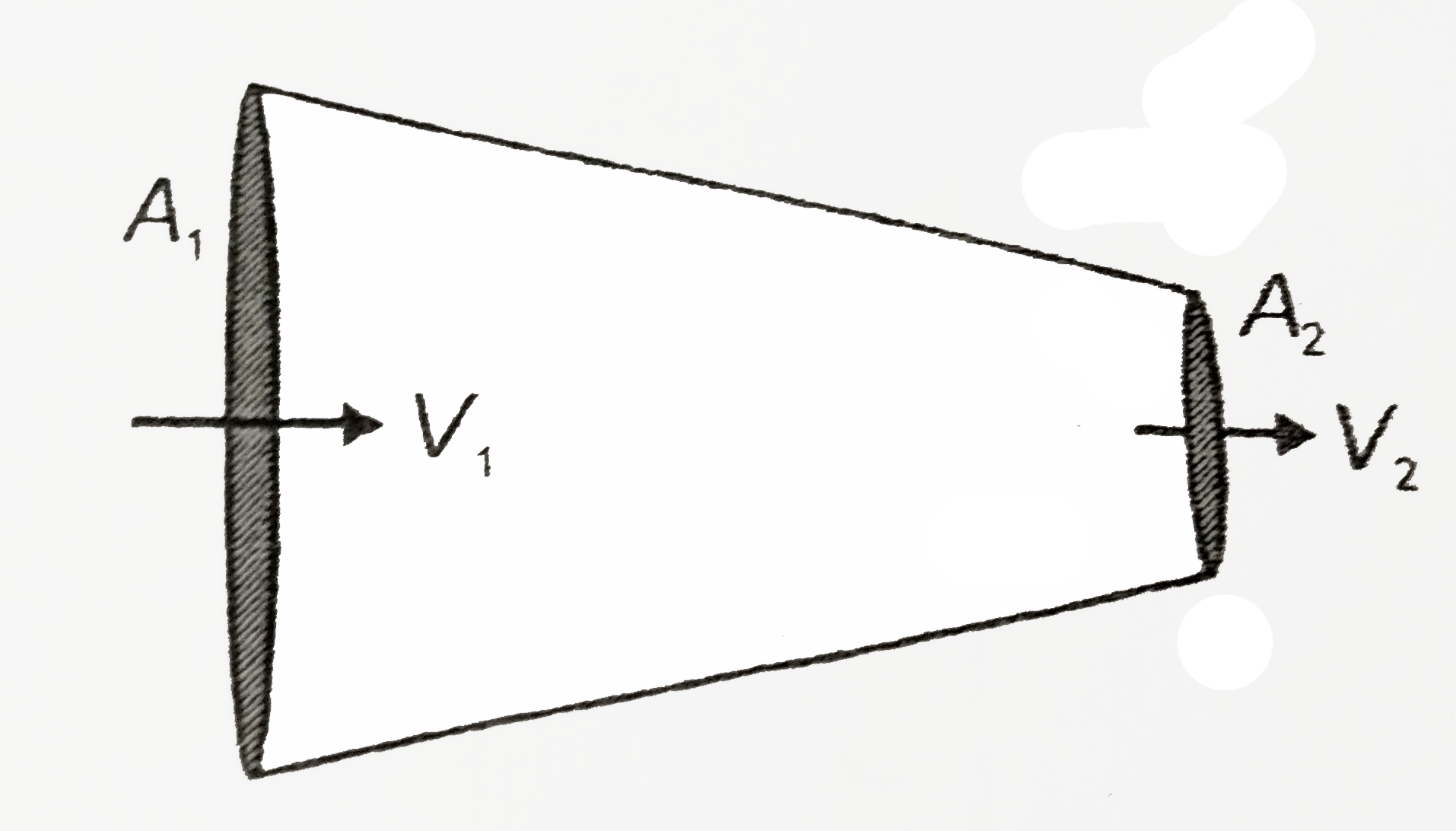
Calculate the rate of flow of glycerine of density 1.25×103kgm−3 through the conical section of a horizontal pipe, if the radii of its ends are 0.1 m and 0.04 m and the pressure drop across its length is 10Nm−2.
According to continuity equation
V2V1=A1A2=r21r22=(0.1)2(0.04)2=254
and, according to Bernoulli.s equation for a horizontal tube, P1+12ρV21=P2+12ρV22
V22−V21=2(P1−P2)2=2×10N/m2(1.25×103kg/m3)=16×10−3m2/s2
but V2=254V(1)=6.25V+1∴[(6.25)2−12]V21=16×10−3m2/s2 or V1≈0.0205m/s
the rate of volume flow=A1V1=π(0.1)2×(0.02)=6.28×10−4m3/s
And the rate of mass flow is dmdt=ρA.V.=(1.25×103kg/m3)×(6.28×10−4m3/s)=0.785kg/s
Similar Questions
Calculate the rate of flow of glycerine of density 1.25×103kgm−3 through the conical section of a pipe, if the radii of its ends are0.1 m and 0.04 m and the pressure drop across its length is 10Nm−2.
View SolutionCalculate the rate of flow of glycerine of density 1.20 ×103kg/m3 through the conical section of a pipe. If the radii of its ends are 0.1 m and 0.02 m and the pressure drop across the length is 10 Nm2.
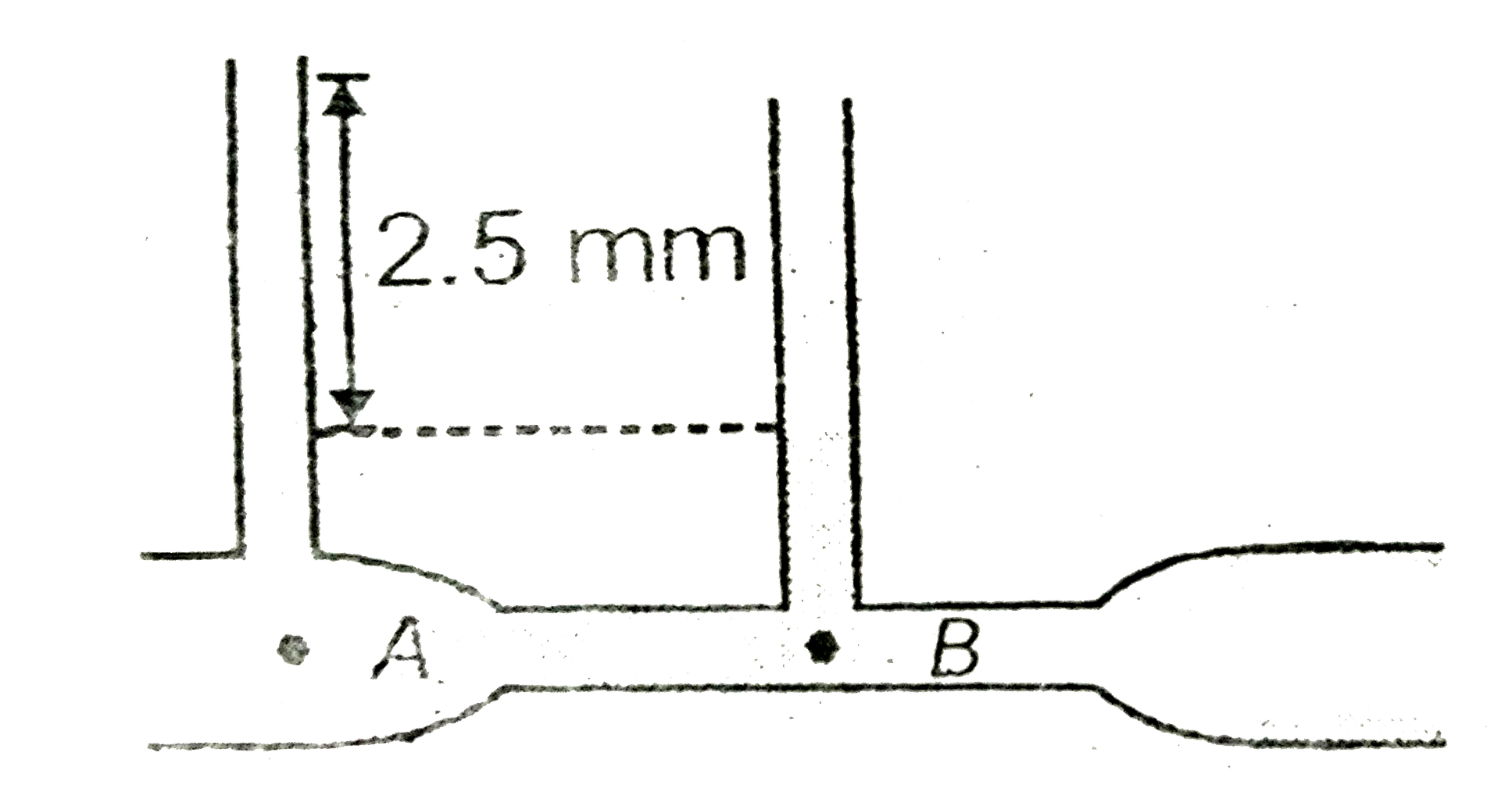
View SolutionIn the figure shown below, a fluid of density 2×103 kg m−3 is flowing in a horizontal pipe. The speed of water at point A is 4 cm s−1, what is its speed at point B?
View SolutionThe radii of curvatures of a convex lens are 0.04 m and 0.04m. Its refractive index is 1.5. Its focal length is
View SolutionCalculate the pH of 1.0×103 M solution of NaCI
View SolutionThe volume of a cuboid is 7.68m3 if its length = 3.2 m and height = 1.0 m find its breadth.
View SolutionTo what height does a liquid of density 0.4×103 kg m−3 and surface tension 0.05 Nm−1 rise in a capillary tube of radius 0.2 mm when dipped in ? [Given cosθ=0.4g=10ms−2]
View SolutionIf the ratio of principal specific heat capacities of a certain gas is 1:4 and its density at STP is 0.09 kgm−3 calculate the values of specific heat capacity at constant pressure and constant volume. [Standard atmospheric pressure =1.01×105Nm−2
View SolutionThe volume of a cuboid is 7.68m3if its length =3.2 m and height = 1.0 m : find its breadth.
View SolutionThe reading of pressure meter attached with a closed water pipe is 3.5×105Nm−2 . On opening the valve of the pipe, the reading of pressure meter is reduced to 3×105Nm−2. Calculate the speed of water flowing out of the pipe.
View Solution
