Calculate the rate of flow of glycerine of density 1.20 $\times 10^{3} k g / m^{3}$ through the conical section of a pipe. If the radii of its ends are 0.1 m and 0.02 m and the pressure drop across the length is 10 $\frac{N}{m^{2}}$ .

Video Solution

Text Solution

Verified by Experts

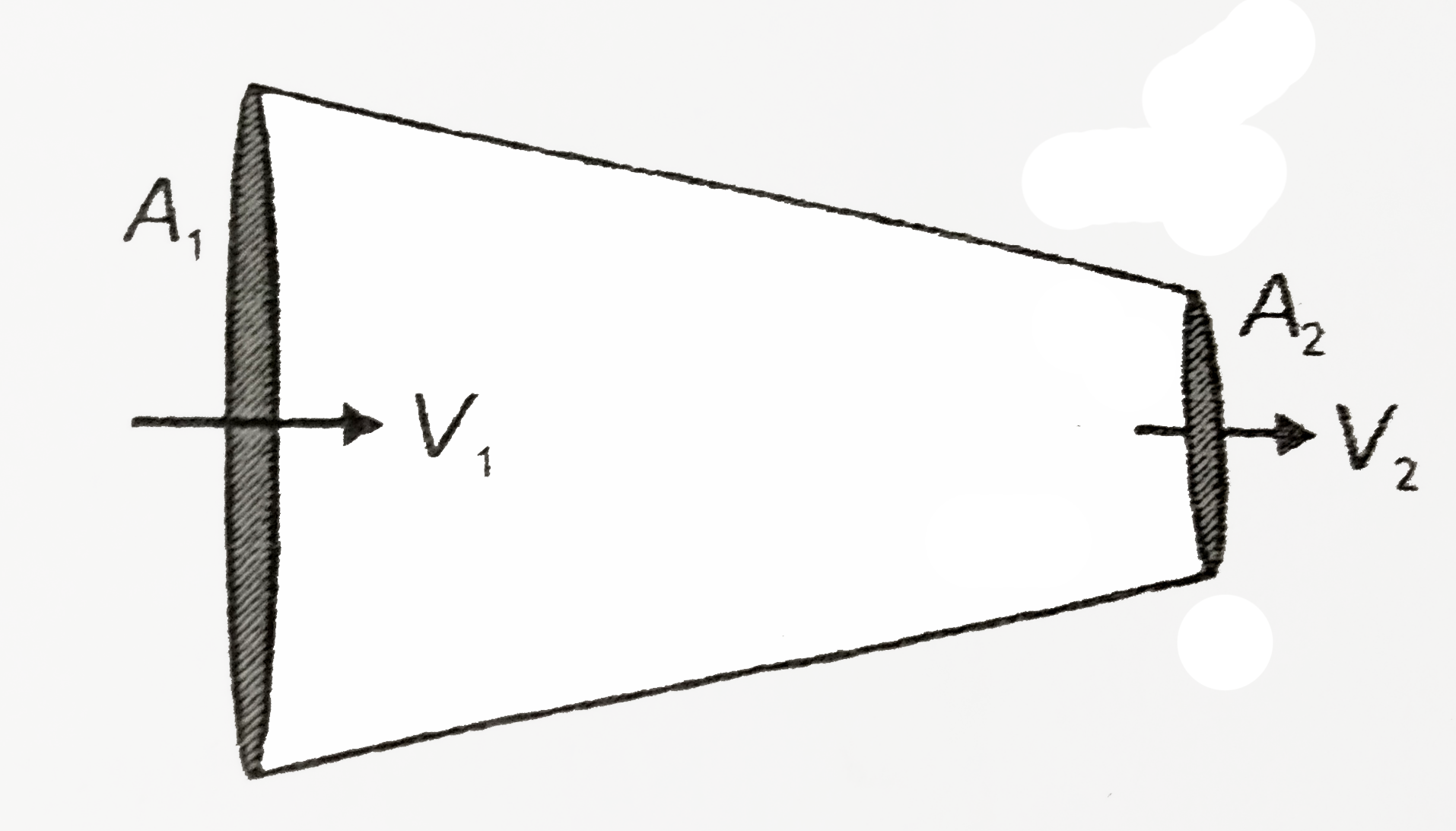
According to continuity equation,
$A_{1} V_{1} = A_{2} V_{2}$
$\Rightarrow \frac{V_{2}}{V_{1}} = \frac{A_{1}}{A_{2}} = \frac{π r_{1}^{2}}{π r_{2}^{2}} = \frac{r_{1}^{2}}{r_{2}^{2}}$
$\Rightarrow \frac{V_{2}}{V_{1}} = {(\frac{r_{1}}{r_{2}})}^{2} = {(\frac{0.10}{0.02})}^{2} = 5^{2} = 25 ... (i)$
and according to Bernoulli's equation
$P_{1} + \frac{1}{2} ρ v_{1}^{2} + ρ g h_{1} = P_{2} + \frac{1}{2} ρ v_{2}^{2} + ρ g h_{2}$
Here pipe is horizontal. So $h_{1} = h_{2}$
$\Rightarrow P_{1} + \frac{1}{2} ρ v_{1}^{2} + ρ g h_{1} = P_{2} + \frac{1}{2} ρ v_{2}^{2} + ρ g h_{1}$
$\Rightarrow P_{1} + \frac{1}{2} ρ v_{1}^{2} = P_{2} + \frac{1}{2} ρ v_{2}^{2}$
$\Rightarrow \frac{1}{2} ρ v_{2}^{2} - \frac{1}{2} ρ v_{1}^{2} = P_{1} - P_{2}$
$\Rightarrow v_{2}^{2} - v_{1}^{2} = \frac{2 (P_{1} P_{2})}{ρ} = \frac{2 \times 10}{1.20 \times 10^{3}} = \frac{20}{1.20 \times 10^{3}}$
$\Rightarrow v_{2}^{2} - v_{1}^{2} = \frac{20}{1200} = \frac{2}{120} = \frac{1}{60} = 16.7 \times 10^{- 3} ... (i i)$
Substituting the value of $V_{2}$ from equation (i) in (ii)
${(25 V_{1})}_{1}^{2} - V_{1}^{2} = 16.7 \times 10^{- 3}$
$\Rightarrow 624 V_{1}^{2} = 16.7 \times 10^{- 3}$
$\Rightarrow v_{1}^{2} = \frac{167 \times 10^{- 4}}{624}$
$\Rightarrow V_{1} = \sqrt{\frac{167}{624}} \times 10^{- 2} m / sec$
So, rate of flow through the tube
$R = A_{1} V_{1} = A_{2} V_{2} = π \times {(0.1)}^{2} \times \sqrt{\frac{167}{624}} \times 10^{- 2}$
$= π \times \sqrt{\frac{167}{624}} \times 10^{- 4}$

Updated on:21/07/2023

The workdone by pressure in forcing $1 m^{3}$ of water through a pipe if the pressure difference across the pipe is $10^{4}$ Pa, is
A $10^{5} J$
B $10^{4} J$
C $10^{3} J$
D $10^{2} J$
Two metal spheres are falling through a liquid of density $2 \times 10^{3} k g / m^{3}$ with the same uniform speed. The material density of sphere 1 and sphere 2 are $8 \times 10^{3} k g / m^{3}$ and $11 \times 10^{3} k g / m^{3}$ respectively. The ratio of their radii is :-
A $\frac{11}{8}$
B $\sqrt{\frac{11}{8}}$
C $\frac{3}{2}$
D $\sqrt{\frac{3}{2}}$
A drop of radius $2 \times 10^{- 5}$ and density $1.2 \times 10^{3} k g / m^{3}$ falls through air. The viscosity of air is $1.8 \times 10^{- 5} N s / m^{2} .$ Neglecting buoyancy due to air, the terminal speed of the drop is
A $2.8 c m / s$
B $3.8 c m / s$
C $4.8 c m / s$
D $5.8 c m / s$